Geometrical Effects on Nonlinear Electrodiffusion in Cell Physiology

Abstract

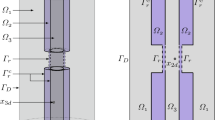
We report here new electrical laws, derived from nonlinear electrodiffusion theory, about the effect of the local geometrical structure, such as curvature, on the electrical properties of a cell. We adopt the Poisson–Nernst–Planck equations for charge concentration and electric potential as a model of electrodiffusion. In the case at hand, the entire boundary is impermeable to ions and the electric field satisfies the compatibility condition of Poisson’s equation. We construct an asymptotic approximation for certain singular limits to the steady-state solution in a ball with an attached cusp-shaped funnel on its surface. As the number of charge increases, they concentrate at the end of cusp-shaped funnel. These results can be used in the design of nanopipettes and help to understand the local voltage changes inside dendrites and axons with heterogeneous local geometry.

Appendix

1.1 Regular Expansion of the PNP Solution when There are an Excess of Positive and a Small Number of Negative Charges

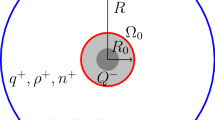
We show that for the concentrations of cations and anions found in the literature (Hille 2001), the leading-order solution of the electrical potential in the bulk can be obtained by considering positive charges only. We assume that the charge of an electrolyte confined in $\tilde{\varOmega }$ consists of identical $N_{p}$ positive and $N_m$ negative ions with density $q_{p}({\varvec{x}})$ and $q_m({\varvec{x}})$ such as

$$\begin{aligned} N_i=\int _{\tilde{\varOmega }}q_i({\tilde{{\varvec{x}}}})\,\mathrm{d}{\tilde{{\varvec{x}}}},\quad \text{ for } \, i \in \{ p,\,m\}, \end{aligned}$$

(117)

where p and m are positive and negative species, respectively. The total charges in $\tilde{\varOmega }$ are the sum

$$\begin{aligned} Q =e( N_{p}-N_m). \end{aligned}$$

(118)

The associated charge densities $\rho _{p}({\varvec{x}},t)$ and $\rho _m({\varvec{x}},t)$ satisfy the boundary value problem for the Nernst–Planck equation

$$\begin{aligned}&D_i\left[ \Delta \rho _i({\tilde{{\varvec{x}}}},t) +\frac{z_ie}{kT} \nabla \left( \rho _i({\tilde{{\varvec{x}}}},t) \nabla \phi ({\tilde{{\varvec{x}}}},t)\right) \right] =\, \frac{\partial \rho _i({\tilde{{\varvec{x}}}},t)}{\partial t}\quad \text{ for }\ {\tilde{{\varvec{x}}}}\in \tilde{\varOmega } \end{aligned}$$

(119)

$$\begin{aligned}&D_i\left[ \frac{\partial \rho _i({\tilde{{\varvec{x}}}},t)}{\partial n}+\frac{z_ie}{kT}\rho _i({\tilde{{\varvec{x}}}},t)\frac{\partial \phi ({\tilde{{\varvec{x}}}},t)}{\partial n}\right] =\,0\quad \text{ for }\ {\tilde{{\varvec{x}}}}\in \partial \tilde{\varOmega } \end{aligned}$$

(120)

$$\begin{aligned}&\rho _i({\tilde{{\varvec{x}}}},0)=\,q_i({\tilde{{\varvec{x}}}})\quad \text{ for }\ {\tilde{{\varvec{x}}}}\in \tilde{\varOmega }, \end{aligned}$$

(121)

where $z_i$ is the valence and $D_i$ is the diffusion coefficient for the ion specie i. The electric potential $\phi ({\tilde{{\varvec{x}}}},t)$ in $\tilde{\varOmega }$ is solution of the Neumann problem for the Poisson equation

$$\begin{aligned} \Delta \phi ({\tilde{{\varvec{x}}}},t)&= -\frac{e}{\varepsilon _r\varepsilon _0}\left( \rho _p({\tilde{{\varvec{x}}}})- \rho _m({\tilde{{\varvec{x}}}})\right) \quad \text{ for }\ {\tilde{{\varvec{x}}}}\in \tilde{\varOmega }\nonumber \\ \frac{\partial \phi ({\varvec{x}},t)}{\partial n}&=-\tilde{\sigma }(\tilde{\varvec{x}},t)\quad \text{ for }\ \tilde{\varvec{x}}\in {\partial \tilde{\varOmega }}, \end{aligned}$$

(122)

where $\tilde{\sigma }({\tilde{{\varvec{x}}}},t)$ is the surface charge density on the boundary $\partial \tilde{\varOmega }$. At steady state, (119) gives

$$\begin{aligned} \rho _i({\tilde{{\varvec{x}}}})= \rho _{i,0}\exp \left( \displaystyle -\frac{z_i e\phi ({\tilde{{\varvec{x}}}})}{k_\mathrm{BT}} \right) \quad \text{ for } i\in \{p\,,\,m\}, \end{aligned}$$

(123)

where $\rho _{i,0}$ is obtained from no-flux boundary condition (120), thus

$$\begin{aligned} \rho _i({\tilde{{\varvec{x}}}})= \frac{ N_i\exp \left( \displaystyle -\frac{z_i e\phi ({\tilde{{\varvec{x}}}})}{k_\mathrm{BT}} \right) }{\displaystyle \int _{\tilde{\varOmega }} \exp \left( \displaystyle -\frac{z_i e\phi ({\varvec{s}})}{k_\mathrm{BT}} \right) \mathrm{d}{\varvec{s}}}\quad \text{ for } i\in \{p,\,m\}. \end{aligned}$$

(124)

Using the nondimensionalized potential $\displaystyle \tilde{u}({\tilde{{\varvec{x}}}})=\frac{e\,\phi ({\tilde{{\varvec{x}}}})}{k_\mathrm{BT}}$, Eq. (123) becomes

$$\begin{aligned} \rho _i({\tilde{{\varvec{x}}}})= \frac{ N_ie^{\displaystyle -z_i\, \tilde{u}({\tilde{{\varvec{x}}}})}}{ \displaystyle \int _{\tilde{\varOmega }} e^{\displaystyle -z_i\, \tilde{u}({\varvec{s}})}\mathrm{d}{\varvec{s}}}\quad \text{ for } i\in \{p,\,m\}. \end{aligned}$$

(125)

Using (122) and (125), we obtain

$$\begin{aligned} -\Delta \tilde{u}({\tilde{{\varvec{x}}}})= & {} \frac{l_\mathrm{B}N_pe^{\displaystyle - \tilde{u}({\tilde{{\varvec{x}}}})}}{ \int _{\tilde{\varOmega }} e^{\displaystyle - \tilde{u}({\varvec{s}})}\, \mathrm{d}{\varvec{s}}}-\frac{l_\mathrm{B} N_me^{\displaystyle \tilde{u}({\tilde{{\varvec{x}}}})}}{ \int _{\tilde{\varOmega }} e^{\displaystyle \tilde{u}({\varvec{s}})}\, \mathrm{d}{\varvec{s}}}\, \text{ in } \, \tilde{\varOmega }\nonumber \\ \frac{\partial u({\tilde{{\varvec{x}}}})}{\partial n}= & {} -\frac{(N_p-N_m) }{|\partial \tilde{\varOmega }| }l_\mathrm{B} \, \text{ on } \, \partial \tilde{\varOmega }, \end{aligned}$$

(126)

where $l_\mathrm{B}$ is the Bjerrum length. Using $\displaystyle {\varvec{x}}=\frac{{\tilde{{\varvec{x}}}}}{R_\mathrm{c}}$ and $\tilde{u}(\tilde{x})=u(x)$ where $R_\mathrm{c}$ is the cusp curvature radius, (126) becomes

$$\begin{aligned} -\Delta {u}({\varvec{x}})= & {} \frac{l_\mathrm{B}N_pe^{\displaystyle - {u}( {\varvec{x}})}}{R_\mathrm{c} \int _{ \varOmega } e^{\displaystyle - {u}({\varvec{s}})}\, \mathrm{d}{\varvec{s}}}-\frac{l_\mathrm{B} N_me^{\displaystyle {u}({\varvec{x}})}}{R_\mathrm{c} \int _{ \varOmega } e^{\displaystyle {u}({\varvec{s}})}\, \mathrm{d}{\varvec{s}}} \quad \text{ in } \, {\varOmega }\nonumber \\ \frac{\partial u( {\varvec{x}})}{\partial n}= & {} -\frac{l_\mathrm{B}(N_p-N_m) }{R_\mathrm{c}|\partial \varOmega | } \quad \text{ on } \, \partial {\varOmega }. \end{aligned}$$

(127)

The small parameter is $\zeta =\displaystyle \frac{N_m}{N_p}\ll 1$ because in the bulk, the concentration of negative charges such as chloride (about 4 mM) is much smaller than positive ones (potassium and sodium account together roughly for 167 mM Hille 2001). A regular expansion of $u({\varvec{x}})$ is

$$\begin{aligned} u({\varvec{x}})= & {} u_0({\varvec{x}})+\zeta u_1({\varvec{x}})+\cdots \end{aligned}$$

(128)

Using (128) in (127), in small $\zeta$ limit, we have

$$\begin{aligned} -\Delta {u_0}({\varvec{x}})= & {} \frac{l_\mathrm{B} N_p e^{\displaystyle - {u_0}( {\varvec{x}})}}{R_\mathrm{c} \int _{ \varOmega } e^{\displaystyle - {u_0}({\varvec{s}})}\, \mathrm{d}{\varvec{s}}}\, \text{ in } \, {\varOmega }\nonumber \\ \frac{\partial u_0( {\varvec{x}})}{\partial n}= & {} -\frac{l_\mathrm{B} N_p }{R_\mathrm{c}|\partial \varOmega | }\, \text{ on } \, \partial {\varOmega }, \end{aligned}$$

(129)

and in $\varOmega$

$$\begin{aligned} \Delta {u_1}({\varvec{x}})= & {} \frac{l_\mathrm{B} N_{p} }{R_\mathrm{c} } \left( \frac{e^{\displaystyle - u_0({\varvec{x}})}}{\int _{ \varOmega } e^{\displaystyle - {u_0}({\varvec{s}})}\, \mathrm{d}{\varvec{s}}}\left( u_1({\varvec{x}})- \frac{\int _{ \varOmega } u_1({\varvec{s}})e^{\displaystyle - {u_0}({\varvec{s}})}\, \mathrm{d}{\varvec{s}}}{\int _{ \varOmega } e^{\displaystyle - {u_0}({\varvec{s}})}\, \mathrm{d}{\varvec{s}}} \right) + \frac{e^{\displaystyle u_0({\varvec{x}})}}{\int _{ \varOmega } e^{\displaystyle {u_0}({\varvec{s}})}\, \mathrm{d}{\varvec{s}}}\right) \nonumber \\ \frac{\partial u_1( {\varvec{x}})}{\partial n}= & {} \frac{l_\mathrm{B}N_{p} }{R_\mathrm{c}|\partial \varOmega | }\, \text{ on } \, \partial {\varOmega }, \end{aligned}$$

(130)

which admit a regular solution. This result shows that the limit of the PNP equation when $\zeta$ tends to zero (small charge limit) gives $v_0({\varvec{x}})$, and thus we conclude that a small amount of negative charges does not perturb the distribution of the total excess of positive charge in the bulk.

1.2 The Numerical Procedure

Numerical solutions were constructed by the COMSOL Multiphysics 5.0 (BVP problems), Maple 2015 (shooting problems) and MATLAB R2015 (conformal mapping). The boundary value problems in 1D, 2D and 3D were solved by the finite elements method in the COMSOL ‘Mathematics’ package. We used an adaptive mesh refinement to ensure numerical convergence for large value of the parameter $\lambda$.

We solved the PDEs by the shooting procedure for boundary value problems using Runge–Kutta fourth-order method, as well as solvers from Maple packages.