Novel Multiplierless Wideband Comb Compensator with High Compensation Capability

Abstract

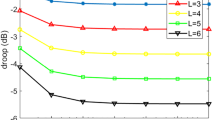
This paper proposes a novel multiplierless comb compensation filter, which has the absolute passband deviation less than 0.1 dB in the wide passband. The compensator consists of a cascade of two simple filter sections, both operating at a low rate. The magnitude characteristics of the two-component filters are synthesized as sinewave functions, in which the main design parameters correspond to the amplitudes of sinewave functions. A systematic procedure is followed to select synthesis parameters, which depend only on the number of cascaded comb filters. In particular, they are independent of the decimation factor. Comparisons with comb compensators from the literature illustrate the benefits of the proposed design.

Appendix

Here, the derivation of (29) is presented in detail.

From (27), we have:

$$\begin{aligned} \left| {H_c (e^{j\omega _k })} \right| <10^{\left| {\delta _d } \right| /40}. \end{aligned}$$

(31)

Using (14), we write:

$$\begin{aligned} \left| {H_c (e^{j\omega _k })} \right| =\left| {H(e^{j\omega _k })G_1 (e^{jM\omega _k })G_2 (e^{jM\omega _k })} \right| , \end{aligned}$$

(32)

where $\omega _{k}$ are arbitrary frequencies in the passband, given by

$$\begin{aligned} \omega _k =\frac{\pi k}{2MN};k=1,\ldots N. \end{aligned}$$

(33)

Placing (32) into (31), we get:

$$\begin{aligned} \left| {H(e^{j\omega _k })G_1 (e^{jM\omega _k })G_2 (e^{jM\omega _k })} \right| <10^{\left| {\delta _d } \right| /40}. \end{aligned}$$

(34)

From (3), we write by noting that the comb magnitude response is positive in the passband:

$$\begin{aligned} \left| H(e^{j{\omega _k}}) \right| =\left[ {\frac{1}{M}\frac{\sin (\omega _k M/2)}{\sin (\omega _k /2)}} \right] ^{K}. \end{aligned}$$

(35)

We rewrite (35) as:

$$\begin{aligned} \left| {H(e^{j{\omega _k}})} \right| \approx \left[ {\frac{1}{M}\frac{\sin (\omega _k M/2)}{\omega _k /2}} \right] ^{K}. \end{aligned}$$

(36)

Placing (33) into (36), we get:

$$\begin{aligned} \left| {H(e^{j{\omega _k}})} \right| \approx \left[ {\frac{\sin (\pi k/(4N))}{\pi k/(4N)}} \right] ^{K}. \end{aligned}$$

(37)

Similarly, using (4), we write:

$$\begin{aligned} \left| {G_2 (e^{j\omega _k M})} \right| =1+B_{2s_k } \sin ^{2}(\omega _k M/2)=1+B_{2s_k } \sin ^{2}(\pi k/(4N)). \end{aligned}$$

(38)

From (34), (37), and (38), we arrive at:

$$\begin{aligned} \left[ {\frac{\sin (\pi k/(4N))}{\pi k/(4N)}} \right] ^{K}G_1 (e^{jM\omega _k })\left[ {1+B_{2s_k } \sin ^{2}(\pi k/(4N))} \right] <10^{\left| {\delta _d } \right| /40}. \end{aligned}$$

(39)

From here, we have:

$$\begin{aligned} \left[ {1+B_{2s_k } \sin ^{2}(\pi k/(4N))} \right] <\frac{\left[ {\frac{\pi k/(4N)}{\sin (\pi k/(4N))}} \right] ^{K}}{G_1 (e^{jM\omega _k })}10^{\left| {\delta _d } \right| /40}. \end{aligned}$$

(40)

Also,

$$\begin{aligned} B_{2s_k } \sin ^{2}(\pi k/(4N))<\frac{-G_1 (e^{jM\omega _k })+\left[ {\frac{\pi k/(4N)}{\sin (\pi k/(4N))}} \right] ^{K}10^{\left| {\delta _d } \right| /40}}{G_1 (e^{jM\omega _k })}, \end{aligned}$$

(41)

and

$$\begin{aligned} B_{2s_k } <\frac{-G_1 (e^{jM\omega _k })+\left[ {\frac{\pi k/(4N)}{\sin (\pi k/(4N))}} \right] ^{K}10^{\left| {\delta _d } \right| /40}}{G_1 (e^{jM\omega _k })\sin ^{2}(\pi k/(4N))}. \end{aligned}$$

(42)

Using (5), we write:

$$\begin{aligned} \left| {G_1 (e^{j\omega _k M})} \right| =1+B_1 \sin ^{2}(\omega _k M/2)=1+B_1 \sin ^{2}(\pi k/(4N)), \end{aligned}$$

(43)

where values $B_{1}$ are given in Table 2.

Finally, from (42) and (43), we arrive at:

$$\begin{aligned} B_{2s_k } <\frac{-\left[ {1+B_1 \sin ^{2}(\pi k/(4N))} \right] +\left[ {\frac{\pi k/(4N)}{\sin (\pi k/(4N))}} \right] ^{K}10^{\left| {\delta _d } \right| /40}}{\left[ {1+B_1 \sin ^{2}(\pi k/(4N))} \right] \sin ^{2}(\pi k/(4N))}, \quad k=1,{\ldots },N .\nonumber \\ \end{aligned}$$

(44)