1 Introduction

The support vector machine (SVM) has been one of the most successful machine learning algorithms (Boser et al. 1992; Cortes and Vapnik 1995; Vapnik 1998). However, in recent practical machine learning applications with less reliable data that contains outliers, non-robustness of the SVM often causes considerable performance deterioration. In robust learning context, outliers indicate observations that have been contaminated, inaccurately recorded, or drawn from different distributions from other normal observations.

Fig. 1
figure 1

Illustrative examples of a standard SVC (support vector classification) and b robust SVC, c standard SVR (support vector regression) and d robust SVR on toy datasets. In robust SVM, the classification and regression results are not sensitive to the two red outliers in the right-hand side of the plots (Color figure online)

Full size image

Figure 1 shows examples of robust SV classification and regression. In classification problems, we regard the instances whose labels are flipped from the ground truth as outliers. As illustrated in Fig. 1a, standard SV classifier may be highly affected by outliers. On the other hand, robust SV classifier can alleviate the effects of outliers as illustrated in Fig. 1b. In regression problems, we regard instances whose output response are highly contaminated than other normal observations as outliers. Standard SV regression tends to produce an unstable result as illustrated in Fig. 1c, while robust SV regression can alleviate the effects of outliers as illustrated in Fig. 1d.

1.1 Existing robust classification and regression methods

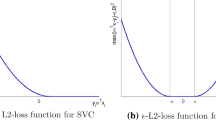
A great deal of efforts have been devoted to improve the robustness of the SVM and other similar learning algorithms (Masnadi-Shiraze and Vasconcelos 2000; Bartlett and Mendelson 2003; Shen et al. 2003; Krause and Singer 2004; Liu et al. 2005; Liu and Shen 2006; Xu et al. 2006; Collobert et al. 2006; Wu and Liu 2007; Masnadi-Shirazi and Vasconcelos 2009; Freund 2009; Yu et al. 2010). In the context of SV classification, so-called Ramp loss function (see Fig. 2a) is introduced for alleviating the effects of outliers. Similarly, robust loss function for SV regression (see Fig. 2b) is also introduced. Robustness properties obtained by replacing the loss functions to these robust ones have been intensively studied in the context of robust statistics.

Fig. 2
figure 2

Robust loss functions for a SV classification and b SV regression. Note that these robust loss functions are essentially non-convex because they are designed to alleviate the effect of outliers. Furthermore, robust loss functions have additional hyper-parameter for controlling the trade-off between robustness and efficiency. For example, in Ramp loss function, one has to determine the breakpoint (the location of the orange circle) of the robust loss function. In plot (a), the breakpoint at margin −1.0 indicates that we regard the instances whose margin is smaller than −1.0 as outliers. Similarly, in plot (b), the breakpoints at ±1.0 indicate that we regard the instances whose absolute residuals are greater than 1.0 as outliers (Color figure online)

Full size image

As illustrated in Fig. 2, robust loss functions have two common properties. First, robust loss functions are essentially non-convex because they are designed to alleviate the effect of outliers.Footnote 1 If one uses a convex loss, even a single outlier can dominate the classification or regression result. Second, robust loss functions have an additional parameter for controlling the trade-off between robustness and efficiency. For example, in Ramp loss function in Fig. 2a, one must determine the breakpoint of the loss function (the location of the orange circle). Since such a tuning parameter governs the influence of outliers on the model, it must be carefully tuned based on the property of noise contained in the data set. Unless one has a clear knowledge about the properties of outliers, one has to tune the tuning parameter by using a model selection method such as cross-validation. These two properties suggest that one must solve many non-convex optimization problems for various values of the tuning parameter.

Unfortunately, existing non-convex optimization algorithms for robust SVM learning are not sufficiently efficient nor stable. The most common approach for solving non-convex optimization problems in robust SV classification and regression is Difference of Convex (DC) programming (Shen et al. 2003; Krause and Singer 2004; Liu et al. 2005; Liu and Shen 2006; Collobert et al. 2006; Wu and Liu 2007), or its special form called Concave Convex Procedure (CCCP) (Yuille and Rangarajan 2002). Since a solution obtained by these general non-convex optimization methods is only one of many local optimal solutions, one has to repeatedly solve the non-convex optimization problems from multiple different initial solutions. Furthermore, due to the non-convexity, robust SVM solutions with slightly different tuning parameter values can be significantly different, which makes the tuning-parameter selection problem highly unstable. To the best of our knowledge, there are no other existing studies that allows us to efficiently obtain stable sequence of multiple local optimal solutions for various tuning parameters values in the context of robust SV classification and regression.

1.2 Our contributions

In this paper, we address efficiency and stability issues of robust SV learning simultaneously by introducing a novel homotopy approach.Footnote 2 First, we introduce parameterized formulations of robust SVC and SVR which bridge the standard SVM and fully robust SVM via a parameter that governs the influence of outliers. Second, we use homotopy methods (Allgower and George 1993; Gal 1995; Ritter 1984; Best 1996) for tracing a path of solutions when the influence of outliers is gradually decreased. We call the parameter as the homotopy parameter and the path of solutions obtained by tracing the homotopy parameter as the outlier path. Figs. 3 and 4 illustrate how the robust loss functions for classification and regression problems can be gradually robustified, respectively.

Our first technical contribution is in analyzing the properties of the outlier path for both classification and regression problems. In particular, we derive the necessary and sufficient conditions for SVC and SVR solutions to be locally optimal (note that the well-known Karush-Khun Tucker (KKT) conditions are only necessary, but not sufficient). Interestingly, the analyses indicate that the outlier paths contain a finite number of discontinuous points. To the best of our knowledge, the above property of robust learning has not been known previously.

Fig. 3
figure 3

An illustration of the parametrized class of problems for robust SV classification (SVC). A loss function in each plot (red one) is characterized by two parameters \(\theta \in [0, 1]\) and \(s \in (-\infty , 0]\), which we call robustness parameters. When \(\theta =1\) or \(s = -\infty \), the loss function is identical with the hinge loss function in standard SVM. On the other hand, when \(\theta =0\) and \(s \ne -\infty \), the loss function is identical with the ramp loss function which has been used in several robust SV learning studies. In this paper, we consider a parametrized formulations of robust SVC which bridges the standard SVC and fully robust SVC via the homotopy parameters \(\theta \) and/or s that governs the influence of outliers. The algorithm we introduce in this paper allows us to compute a path of solutions when we continuously change these homotopy parameters. In the top row and the bottom row, we consider paths of solutions with respect to the homotopy parameter \(\theta \) and s, respectively. a Homotopy computation with decreasing \(\theta \) from 1 to 0. b Homotopy computation with increasing s from \(-\infty \) to 0 (Color figure online)

Full size image
Fig. 4
figure 4

An illustration of the parametrized class of problems for robust SV regression (SVR). A loss function in each plot (red one) is characterized by two parameters \(\theta \in [0, 1]\) and \(|s| \in [0, \infty )\), which we call robustness parameters. When \(\theta =1\) or \(|s| = 0\), the loss function is identical with the loss function of least absolute deviation (LAD) regression. On the other hand, when \(\theta =0\) and \(|s| \ne \infty \), the loss function is a robust function in which the influences of outliers are bounded. In this paper, we also consider a parametrized formulations of robust SVR which bridges the standard SVR and the robust SVR via the homotopy parameters \(\theta \) and/or |s| that governs the influence of outliers. The algorithm we introduce in this paper allows us to compute a path of solutions when we continuously change these homotopy parameters. In the top row and the bottom row, we consider paths of solutions with respect to the homotopy parameter \(\theta \) and s, respectively. a Homotopy computation with decreasing \(\theta \) from 1 to 0. b Homotopy computation with decreasing s from \(-\infty \) to 0 (Color figure online)

Full size image

Our second contribution is to develop an efficient algorithm for actually computing the outlier path based on the above theoretical investigation of the geometry of robust SVM solutions. Here, we use parametric programming technique (Allgower and George 1993; Gal 1995; Ritter 1984; Best 1996), which is often used for computing the regularization path in machine learning literature. The main technical challenge here is how to handle the discontinuous points in the outlier path. We overcome this difficulty by precisely analyzing the necessary and sufficient conditions for the local optimality. We develop an algorithm that can precisely detect such discontinuous points, and jump to find a strictly better local optimal solution.

Experimental results indicate that our proposed method can find better robust SVM solutions more efficiently than alternative method based on CCCP. We conjecture that there are two reasons why favorable results can be obtained with our method. At first, the outlier path shares similar advantage as simulated annealing (Hromkovic 2001). Simulated annealing is known to find better local solutions in many non-convex optimization problems by solving a sequence of solutions along with so-called temperature parameter. If we regard the homotopy parameter as the temperature parameter, our outlier path algorithm can be interpreted as simulated annealing with infinitesimal step size (as we explain in the following sections, our algorithm represents the path of local solutions as a function of the homotopy parameter). Since our algorithm provides the path of local solutions, unlike other non-convex optimization algorithms such as CCCP, two solutions with slightly different homotopy parameter values tend to be similar, which makes the tuning parameter selection stable. According to our experiments, choice of the homotopy parameter is quite sensitive to the generalization performances. Thus, it is important to finely tune the homotopy parameter. Since our algorithm can compute the path of solutions, it is much more computationally efficient than running CCCP many times at different homotopy parameter values.

1.3 Organization of the paper

After we formulate robust SVC and SVR as parametrized optimization problems in Sect. 2, we derive in Sect. 3 the necessary and sufficient conditions for a robust SVM solution to be locally optimal, and show that there exist a finite number of discontinuous points in the local solution path. We then propose an efficient algorithm in Sect. 4 that can precisely detect such discontinuous points and jump to find a strictly better local optimal solution. In Sect. 5, we experimentally demonstrate that our proposed method, named the outlier path algorithm, outperforms the existing robust SVM algorithm based on CCCP or DC programming. Finally, we conclude in Sect. 6.

This paper is an extended version of our preliminary conference paper presented at ICML 2014 (Suzumura et al. 2014). In this paper, we have extended our robusitification path framework to the regression problem, and many more experimental evaluations have been conducted. To the best of our knowledge, the homotopy method (Allgower and George 1993; Gal 1995; Ritter 1984; Best 1996) is first used in our preliminary conference paper in the context of robust learning, So far, homotopy-like methods have been (often implicitly) used for non-convex optimization problems in the context of sparse modeling (Zhang 2010; Mazumder et al. 2011; Zhou et al. 2012) and semi-supervised learning (Ogawa et al. 2013).

2 Parameterized formulation of robust SVM

In this section, we first formulate robust SVMs for classification and regression problems, which we denote by robust SVC (SV classification) and robust SVR (SV regression), respectively. Then, we use parameterized formulation both for robust SVC and SVR, where the parameter governs the influence of outlieres to the model. The problem is reduced to ordinary non-robust SVM at one end of the parameter, while the problem corresponds to fully-robust SVM at the other end of the parameter. In the following sections, we develop algorithms for computing the path of local optimal solutions when the parameter is changed form one end to the other.

2.1 Robust SV classification

Let us consider a binary classification problem with n instances and d features. We denote the training set as \(\{({\varvec{x}}_i, y_i)\}_{i \in \mathbb {N}_n}\) where \({\varvec{x}}_i \in \mathcal {X}\) is the input vector in the input space \(\mathcal {X}\subset \mathbb {R}^d\), \(y_i \in \{-1, 1\}\) is the binary class label, and the notation \(\mathbb {N}_n := \{1, \ldots , n\}\) represents the set of natural numbers up to n. We write the decision function as

$$\begin{aligned} f({\varvec{x}}) := {\varvec{w}}^\top {\varvec{\phi }}({\varvec{x}}), \end{aligned}$$
(1)

where \({\varvec{\phi }}\) is the feature map implicitly defined by a kernel \({\varvec{K}}\), \({\varvec{w}}\) is a vector in the feature space, and \(^\top \) denotes the transpose of vectors and matrices.

We introduce the following class of optimization problems parameterized by \(\theta \) and s:

$$\begin{aligned} \min _{{\varvec{w}}} ~ \frac{1}{2}\Vert {\varvec{w}} \Vert ^2 + C \sum _{i = 1}^n \ell (y_i f({\varvec{x}}_i); ~\theta , s), \end{aligned}$$
(2)

where \(C > 0\) is the regularization parameter which controls the balance between the first regularization term and the second loss term. The loss function \(\ell \) is characterized by a pair of parameters \(\theta \in [0, 1]\) and \(s \le 0\) as

$$\begin{aligned} \ell (z; ~\theta ,s) := \left\{ \begin{array}{ll} [0, 1 - z]_+, &{} z \ge s, \\ 1 - \theta z - s, &{} z < s, \\ \end{array} \right. \end{aligned}$$
(3)

where \([z]_+ := \max \{0, z\}\). We refer to \(\theta \) and s as the homotopy parameters. Figure 3 shows the loss functions for several \(\theta \) and s. Note that when \(\theta = 1\) or \(s = \infty \), the optimization problem (2) is equivalent to the standard formulation of SVC, in particular, so-called soft-margin SVC. In this case, the loss function is reduced to the well-known hinge loss function, which linearly penalizes \(1 - y_i f({\varvec{x}}_i)\) when \(y_i f({\varvec{x}}_i) \le 1\), and gives no penalty for \(y_i f({\varvec{x}}_i) > 1\) (the left-most column in Fig. 3). The input vector \({\varvec{x}}_i\) having \(y_i f({\varvec{x}}_i) \le 1\) at the final solution is called a support vector by which the resulting decision boundary is defined, while the other input vectors do not effect on the boundary because they have no effect on the objective function. The first homotopy parameter \(\theta \) can be interpreted as the weight for an outlier: \(\theta = 1\) indicates that the influence of an outlier is the same as an inlier, while \(\theta = 0\) indicates that outliers are completely ignored. The second homotopy parameter \(s \le 0\) can be interpreted as the threshold for deciding outliers and inliers. When \(\theta = 0\) and \(s = 0\), the loss function is reduced to the ramp loss function (the right-most column in Fig. 3) to which we have referred as fully robust SVM. A variety of robust loss functions, including the functions that we employed here, have appeared in Bartlett and Mendelson (2003).

In the following sections, we consider two types of homotopy methods. In the first method, we fix \(s = 0\), and gradually change \(\theta \) from 1 to 0 (see the top five plots in Fig. 3). In the second method, we fix \(\theta = 0\) and gradually change s from \(-\infty \) to 0 (see the bottom five plots in Fig. 3). The optimization 2 is a convex problem when \(\theta = 1\) or \(s = - \infty \), in which \(\ell \) is the hinge loss, while it is non-convex when \(\theta = 0\) and \(s = 0\), in which \(\ell \) is the ramp loss. Therefore, each of the above two homotopy methods can be interpreted as the process of tracing a sequence of solutions when the optimization problem is gradually modified from convex to non-convex. By doing so, we expect to find good local optimal solutions because such a process can be interpreted as simulated annealing  (Hromkovic 2001). In addition, we can adaptively control the degree of robustness by selecting the best \(\theta \) or s based on some model selection scheme.

2.2 Robust SV regression

Let us next consider a regression problem. We denote the training set of the regression problem as \(\{({\varvec{x}}_i, y_i)\}_{i \in \mathbb {N}_n}\), where the input \({\varvec{x}}_i \in \mathcal {X}\) is the input vector as the classification case, while the output \(y_i \in \mathbb {R}\) is a real scalar. We consider a regression function \(f({\varvec{x}})\) in the form of (1). SV regression is formulated as

$$\begin{aligned} \min _{{\varvec{w}}} ~ \frac{1}{2}\Vert {\varvec{w}} \Vert ^2 + C \sum _{i = 1}^n \ell (y_i - f({\varvec{x}}_i); ~\theta , s), \end{aligned}$$
(4)

where \(C > 0\) is the regularization parameter, and the loss function \(\ell \) is defined as

$$\begin{aligned} \ell (z; ~\theta ,s) := \left\{ \begin{array}{ll} |z|, &{} |z| < s, \\ (|z| - s) \theta + s, &{} |z| \ge s. \\ \end{array} \right. \end{aligned}$$
(5)

The loss function in (5) has two parameters \(\theta \in [0, 1]\) and \(s \in [0, \infty )\) as the classification case. Figure 4 shows the loss functions for several \(\theta \) and s.

3 Local optimality

In order to use the homotopy approach, we need to clarify the continuity of the local solution path. To this end, we investigate several properties of local solutions of robust SVM, and derive the necessary and sufficient conditions. Interestingly, our analysis reveals that the local solution path has a finite number of discontinuous points. The theoretical results presented here form the basis of our novel homotopy algorithm given in the next section that can properly handle the above discontinuity issue. We first discuss the local optimality of robust SVC in detail in Sects. 3.1 and 3.2, and then present the corresponding result of robust SVR briefly in Sect. 3.3. Here we call a solution to be locally optimal if there is no strictly better feasible solutions in its neighborhood.

3.1 Conditionally optimal solutions (for robust SVC)

The basic idea of our theoretical analysis is to reformulate the robust SVC learning problem as a combinatorial optimization problem. We consider a partition of the instances \(\mathbb {N}_n := \{1, \ldots , n\}\) into two disjoint sets \(\mathcal {I}\) and \(\mathcal {O}\). The instances in \(\mathcal {I}\) and \(\mathcal {O}\) are defined as \(\mathcal {I}\)nliers and \(\mathcal {O}\)utliers, respectively. Here, we restrict that the margin \(y_i f({\varvec{x}}_i)\) of an inlier should be larger than or equal to s, while that of an outlier should be smaller than or equal toFootnote 3 s. We denote the partition as \(\mathcal {P}:= \{\mathcal {I}, \mathcal {O}\} \in 2^{\mathbb {N}_n}\), where \(2^{\mathbb {N}_n}\) is the power setFootnote 4 of \(\mathbb {N}_n\). Given a partition \(\mathcal {P}\), the above restrictions define the feasible region of the solution f in the form of a convex polytope:

$$\begin{aligned} \mathrm{pol}({\mathcal {P}};s) := \Biggl \{f ~ \Biggl | \begin{array}{ll} y_i f({\varvec{x}}_i) \ge s, &{} i \in \mathcal {I}\\ y_i f({\varvec{x}}_i) \le s, &{} i \in \mathcal {O}\end{array} \Biggr \}. \end{aligned}$$
(6)

Using the notion of the convex polytopes, the optimization problem (2) can be rewritten as

$$\begin{aligned} \min _{{\mathcal {P}} \in 2^{\mathbb {N}_n}} \Biggl ( \min _{f \in \mathrm{pol}({\mathcal {P}};s)} J_{{\mathcal {P}}}(f;\theta ) \Biggr ), \end{aligned}$$
(7)

where the objective function \(J_{{\mathcal {P}}}\) is defined asFootnote 5

$$\begin{aligned} J_{{\mathcal {P}}}(f;\theta ) := \frac{1}{2} || {\varvec{w}} ||_2^2 + C \left( \sum _{i \in \mathcal {I}}[1 - y_i f({\varvec{x}}_i)]_+ + \theta \sum _{i \in \mathcal {O}}[1 - y_i f({\varvec{x}}_i)]_+ \right) . \end{aligned}$$

Note that the right hand side depends on \(\mathcal {P}\) though \(\mathcal {I}\) and \(\mathcal {O}\).

When the partition \({\mathcal {P}}\) is fixed, it is easy to confirm that the inner minimization problem of (7) is a convex problem.

Definition 1

(Conditionally optimal solutions) Given a partition \({\mathcal {P}}\), the solution of the following convex problem is said to be the conditionally optimal solution:

$$\begin{aligned} f^*_{{\mathcal {P}}} := \mathop {\mathrm{argmin}}\limits _{f \in \mathrm{pol}({\mathcal {P}};s)} J_{{\mathcal {P}}}(f;\theta ). \end{aligned}$$
(8)

The formulation in (7) is interpreted as a combinatorial optimization problem of finding the best solution from all the \(2^n\) conditionally optimal solutions \(f^*_{{\mathcal {P}}}\) corresponding to all possible \(2^n\) partitions.Footnote 6

Using the representer theorem or convex optimization theory, we can show that any conditionally optimal solution can be written as

$$\begin{aligned} f^*_{{\mathcal {P}}}({\varvec{x}}) := \sum _{j \in \mathbb {N}_n} \alpha ^*_j y_j K({\varvec{x}}, {\varvec{x}}_j), \end{aligned}$$
(9)

where \(\{\alpha ^*_j\}_{j \in \mathbb {N}_n}\) are the optimal Lagrange multipliers. The following lemma summarizes the KKT optimality conditions of the conditionally optimal solution \(f^*_{\mathcal {P}}\).

Lemma 2

The KKT conditions of the convex problem (8) is written as

$$\begin{aligned} y_i f^*_{{\mathcal {P}}}({\varvec{x}}_i) > 1 ~\Rightarrow & {} ~ \alpha _i^* = 0, \end{aligned}$$
(10a)
$$\begin{aligned} y_i f^*_{{\mathcal {P}}}({\varvec{x}}_i) = 1 ~\Rightarrow & {} ~ \alpha _i^* \in [0, C], \end{aligned}$$
(10b)
$$\begin{aligned} s< y_i f^*_{{\mathcal {P}}}({\varvec{x}}_i) < 1 ~\Rightarrow & {} ~ \alpha _i^* = C, \end{aligned}$$
(10c)
$$\begin{aligned} y_i f^*_{{\mathcal {P}}}({\varvec{x}}_i) = s, i \in \mathcal {I}~\Rightarrow & {} ~ \alpha _i^* \ge C, \end{aligned}$$
(10d)
$$\begin{aligned} y_i f^*_{{\mathcal {P}}}({\varvec{x}}_i) = s, i \in \mathcal {O}~\Rightarrow & {} ~ \alpha _i^* \le C \theta , \end{aligned}$$
(10e)
$$\begin{aligned} y_i f^*_{{\mathcal {P}}}({\varvec{x}}_i) < s ~\Rightarrow & {} ~ \alpha _i^* = C \theta . \end{aligned}$$
(10f)

The proof is presented in Appendix 7.

3.2 The necessary and sufficient conditions for local optimality (for Robust SVC)

From the definition of conditionally optimal solutions, it is clear that a local optimal solution must be conditionally optimal within the convex polytope \(\mathrm{pol}({\mathcal {P}};s)\). However, the conditional optimality does not necessarily indicate the local optimality as the following theorem suggests.

Theorem 3

For any \(\theta \in [0, 1)\) and \(s \le 0\), consider the situation where a conditionally optimal solution \(f^*_{{\mathcal {P}}}\) is at the boundary of the convex polytope \(\mathrm{pol}({\mathcal {P}};s)\), i.e., there exists at least an instance such that \(y_i f^*_{{\mathcal {P}}}({\varvec{x}}_i) = s\).In this situation, if we define a new partition \(\tilde{\mathcal {P}} := \{\tilde{\mathcal {I}}, \tilde{\mathcal {O}}\}\) as

$$\begin{aligned} \tilde{\mathcal {I}} \leftarrow \mathcal {I}\setminus \{ i \in \mathcal {I}| y_i f^*({\varvec{x}}_i)= & {} s \} \cup \{ i \in \mathcal {O}| y_i f^*({\varvec{x}}_i) = s \}, \end{aligned}$$
(11a)
$$\begin{aligned} \tilde{\mathcal {O}} \leftarrow \mathcal {O}\setminus \{ i \in \mathcal {O}| y_i f^*({\varvec{x}}_i)= & {} s \} \cup \{ i \in \mathcal {I}| y_i f^*({\varvec{x}}_i) = s \}, \end{aligned}$$
(11b)

then the new conditionally optimal solution \(f^*_{\tilde{\mathcal {P}}}\) is strictly better than the original conditionally optimal solution \(f^*_{\mathcal {P}}\), i.e.,

$$\begin{aligned} J_{\tilde{\mathcal {P}}}(f^*_{\tilde{\mathcal {P}}};\theta ) < J_{\mathcal {P}}(f^*_{\mathcal {P}};\theta ). \end{aligned}$$
(12)

The proof is presented in Appendix 8. Theorem 3 indicates that if \(f^*_{{\mathcal {P}}}\) is at the boundary of the convex polytope \(\mathrm{pol}({\mathcal {P}};s)\), i.e., if there is one or more instances such that \(y_i f^*_{\mathcal {P}} ({\varvec{x}}_i) = s\), then \(f^*_{{\mathcal {P}}}\) is NOT locally optimal because there is a strictly better solution in the opposite side of the boundary.

The following theorem summarizes the necessary and sufficient conditions for local optimality. Note that, in non-convex optimization problems, the KKT conditions are necessary but not sufficient in general.

Theorem 4

For \(\theta \in [0, 1)\) and \(s \le 0\),

$$\begin{aligned}&y_i f^*({\varvec{x}}_i) > 1 \Rightarrow \alpha _i^* = 0, \end{aligned}$$
(13a)
$$\begin{aligned}&y_i f^*({\varvec{x}}_i) = 1 \Rightarrow \alpha _i^* \in [0, C], \end{aligned}$$
(13b)
$$\begin{aligned}&s< y_i f^*({\varvec{x}}_i) < 1 \Rightarrow \alpha _i^* = C, \end{aligned}$$
(13c)
$$\begin{aligned}&y_i f^*({\varvec{x}}_i) < s \Rightarrow \alpha _i^* = C \theta , \end{aligned}$$
(13d)
$$\begin{aligned}&y_i f^*({\varvec{x}}_i) \ne s, \ \forall i \in \mathbb {N}_n, \end{aligned}$$
(13e)

are necessary and sufficient for \(f^*\) to be locally optimal.

The proof is presented in Appendix 9. The condition (13e) indicates that the solution at the boundary of the convex polytope is not locally optimal. Figure 5 illustrates when a conditionally optimal solution can be locally optimal with a certain \(\theta \) or s.

Theorem 4 suggests that, whenever the local solution path computed by the homotopy approach encounters a boundary of the current convex polytope at a certain \(\theta \) or s, the solution is not anymore locally optimal. In such cases, it is better to search a local optimal solution at that \(\theta \) or s, and restart the local solution path from the new one. In other words, the local solution path has discontinuity at that \(\theta \) or s. Fortunately, Theorem 3 tells us how to handle such a situation. If the local solution path arrives at the boundary, it can jump to the new conditionally optimal solution \(f^*_{\tilde{\mathcal {P}}}\) which is located on the opposite side of the boundary. This jump operation is justified because the new solution is shown to be strictly better than the previous one. Figure 5c, d illustrate such a situation.

Fig. 5
figure 5

Solution space of robust SVC. a The arrows indicate a local solution path when \(\theta \) is gradually moved from \(\theta _1\) to \(\theta _5\) (see Sect. 4 for more details). b \(f^*_\mathcal {P}\) is locally optimal if it is at the strict interior of the convex polytope \(\mathrm{pol}({\mathcal {P}};s)\). c If \(f^*_\mathcal {P}\) exists at the boundary, then \(f^*_\mathcal {P}\) is feasible, but not locally optimal. A new convex polytope \(\mathrm{pol}({\tilde{\mathcal {P}}};s)\) defined in the opposite side of the boundary is shown in yellow. d A strictly better solution exists in \(\mathrm{pol}({\tilde{\mathcal {P}}};s)\) (Color figure online)

Full size image

3.3 Local optimality of SV regression

In order to derive the necessary and sufficient conditions of the local optimality in robust SVR, with abuse of notation, let us consider a partition of the instances \(\mathbb {N}_n\) into two disjoint sets \({\mathcal {I}}\) and \({\mathcal {O}}\), which represent inliers and outliers, respectively. In regression problems, an instance \(({\varvec{x}}_i, y_i)\) is regarded as an outlier if the absolute residual \(|y_i - f({\varvec{x}}_i)|\) is sufficiently large. Thus, we define inliers and outliers of regression problem as

$$\begin{aligned} {\mathcal {I}}:= & {} \{i \in \mathbb {N}_n |~ |y_i - f({\varvec{x}}_i)| \le s\}, \\ {\mathcal {O}}:= & {} \{i \in \mathbb {N}_n |~ |y_i - f({\varvec{x}}_i)| \ge s\}. \end{aligned}$$

Given a partition \(\mathcal {P}:= \{\mathcal {I}, \mathcal {O}\} \in 2^{\mathbb {N}_n}\), the feasible region of the solution f is represented as a convex polytope:

$$\begin{aligned} \mathrm{pol}(\mathcal {P}; s) := \Biggl \{f ~ \Biggl | \begin{array}{ll} |y_i - f({\varvec{x}}_i)| \le s, &{} i \in {\mathcal {I}}, \\ |y_i - f({\varvec{x}}_i)| \ge s, &{} i \in {\mathcal {O}} \end{array} \Biggr \}. \end{aligned}$$
(14)

Then, as in the classification case, the optimization problem (4) can be rewritten as

$$\begin{aligned} \min _{\mathcal {P}} \Biggl ( \min _{f \in \mathrm{pol}({\mathcal {P}};s)} J_{{\mathcal {P}}}(f;\theta ) \Biggr ), \end{aligned}$$
(15)

where the objective function \(J_{\mathcal {P}}\) is defined as

$$\begin{aligned} J_{\mathcal {P}}(f; \theta ) := \frac{1}{2} || {\varvec{w}} ||_2^2 + C \left( \sum _{i \in {\mathcal {I}}}|y_i - f({\varvec{x}}_i)| + \theta \sum _{i \in {\mathcal {O}}}|y_i - f({\varvec{x}}_i)| \right) . \end{aligned}$$

Since the inner problem of (15) is a convex problem, any conditionally optimal solution can be written as

$$\begin{aligned} f^*_{{\mathcal {P}}}({\varvec{x}}) := \sum _{j \in \mathbb {N}_n} \alpha ^*_j K({\varvec{x}}, {\varvec{x}}_j). \end{aligned}$$
(16)

The KKT conditions of \(f^*_{{\mathcal {P}}}({\varvec{x}})\) are written as

$$\begin{aligned} |y_i - f^*_{{\mathcal {P}}}({\varvec{x}}_i)| = 0 ~\Rightarrow & {} ~ 0 \le |\alpha _i^*| \le C, \end{aligned}$$
(17a)
$$\begin{aligned} 0 \le |y_i - f^*_{{\mathcal {P}}}({\varvec{x}}_i)| < s ~\Rightarrow & {} ~ |\alpha _i^*| = C, \end{aligned}$$
(17b)
$$\begin{aligned} |y_i - f^*_{{\mathcal {P}}}({\varvec{x}}_i)| = s, i \in {\mathcal {I}} ~\Rightarrow & {} ~ |\alpha _i^*| \ge C, \end{aligned}$$
(17c)
$$\begin{aligned} |y_i - f^*_{{\mathcal {P}}}({\varvec{x}}_i)| = s, i \in {\mathcal {O}} ~\Rightarrow & {} ~ |\alpha _i^*| \le \theta C, \end{aligned}$$
(17d)
$$\begin{aligned} |y_i - f^*_{{\mathcal {P}}}({\varvec{x}}_i)| > s ~\Rightarrow & {} ~ |\alpha _i^*| = \theta C. \end{aligned}$$
(17e)

Based on the same discussion as Sect. 3.2, the necessary and sufficient conditions for the local optimality of robust SVR are summarized as the following theorem:

Theorem 5

For \(\theta \in [0, 1)\) and \(s \ge 0\),

$$\begin{aligned}&|y_i - f^*_{{\mathcal {P}}}({\varvec{x}}_i)| = 0 ~ \Rightarrow ~ 0 \le |\alpha _i^*| \le C, \end{aligned}$$
(18a)
$$\begin{aligned}&0 \le |y_i - f^*_{{\mathcal {P}}}({\varvec{x}}_i)| < s ~ \Rightarrow ~ |\alpha _i^*| = C, \end{aligned}$$
(18b)
$$\begin{aligned}&|y_i - f^*_{{\mathcal {P}}}({\varvec{x}}_i)| > s ~ \Rightarrow ~ |\alpha _i^*| = \theta C, \end{aligned}$$
(18c)
$$\begin{aligned}&|y_i - f^*_{{\mathcal {P}}}({\varvec{x}}_i)| \ne s. \end{aligned}$$
(18d)

are necessary and sufficient for \(f^*\) to be locally optimal.

We omit the proof of this theorem because they can be easily derived in the same way as Theorem 4.

4 Outlier path algorithm

Based on the analysis presented in the previous section, we develop a novel homotopy algorithm for robust SVM. We call the proposed method the outlier-path (OP) algorithm. For simplicity, we consider homotopy path computation involving either \(\theta \) or s, and denote the former as OP-\(\theta \) and the latter as OP-s. OP-\(\theta \) computes the local solution path when \(\theta \) is gradually decreased from 1 to 0 with fixed \(s = 0\), while OP-s computes the local solution path when s is gradually increased from \(-\infty \) to 0 with fixed \(\theta = 0\).

The local optimality of robust SVM in the previous section shows that the path of local optimal solutions has finite discontinuous points that satisfy (13e) or (5). Below, we introduce an algorithm that appropriately handles those discontinuous points. In this section, we only describe the algorithm for robust SVC. All the methodologies described in this section can be easily extended to robust SVR counterpart.

4.1 Overview

figure a

The main flow of the OP algorithm is described in Algorithm 1. The solution f is initialized by solving the standard (convex) SVM, and the partition \(\mathcal {P}:= \{\mathcal {I}, \mathcal {O}\}\) is defined to satisfy the constraints in (6). The algorithm mainly switches over the two steps called the continuous step (C-step) and the discontinuous step (D-step).

In the C-step (Algorithm 2), a continuous path of local solutions is computed for a sequence of gradually decreasing \(\theta \) (or increasing s) within the convex polytope \(\mathrm{pol}(\mathcal {P};s)\) defined by the current partition \(\mathcal {P}\). If the local solution path encounters a boundary of the convex polytope, i.e., if there exists at least an instance such that \(y_i f({\varvec{x}}_i) = s\), then the algorithm stops updating \(\theta \) (or s) and enters the D-step.

In the D-step (Algorithm 3), a better local solution is obtained for fixed \(\theta \) (or s) by solving a convex problem defined over another convex polytope in the opposite side of the boundary (see Fig. 5d). If the new solution is again at a boundary of the new polytope, the algorithm repeatedly calls the D-step until it finds the solution in the strict interior of the current polytope.

The C-step can be implemented by any homotopy algorithms for solving a sequence of quadratic problems (QP). In OP-\(\theta \), the local solution path can be exactly computed because the path within a convex polytope can be represented as piecewise-linear functions of the homotopy parameter \(\theta \). In OP-s, the C-step is trivial because the optimal solution is shown to be constant within a convex polytope. In Sects. 4.2 and 4.3, we will describe the details of our implementation of the C-step for OP-\(\theta \) and OP-s, respectively.

In the D-step, we only need to solve a single quadratic problem (QP). Any QP solver can be used in this step. We note that the warm-start approach (DeCoste and Wagstaff 2000) is quite helpful in the D-step because the difference between two conditionally optimal solutions in adjacent two convex polytopes is typically very small. In Sect. 4.4, we describe the details of our implementation of the D-step. Figure 6 illustrates an example of the local solution path obtained by OP-\(\theta \).

figure b
Fig. 6
figure 6

An example of the local solution path by OP-\(\theta \) on a simple toy data set (with \(C = 200\)). The paths of four Lagrange multipliers \(\alpha ^*_1, \ldots , \alpha ^*_4\) are plotted in the range of \(\theta \in [0, 1]\). Open circles represent the discontinuous points in the path. In this simple example, we had experienced three discontinuous points at \(\theta = 0.37, 0.67\) and 0.77

Full size image
figure c

4.2 Continuous-step for OP-\(\theta \)

In the C-step, the partition \(\mathcal {P}:= \{\mathcal {I}, \mathcal {O}\}\) is fixed, and our task is to solve a sequence of convex quadratic problems (QPs) parameterized by \(\theta \) within the convex polytope \(\mathrm{pol}(\mathcal {P};s)\). It has been known in optimization literature that a certain class of parametric convex QP can be exactly solved by exploiting the piecewise linearity of the solution path (Best 1996). We can easily show that the local solution path of OP-\(\theta \) within a convex polytope is also represented as a piecewise-linear function of \(\theta \). The algorithm presented here is similar to the regularization path algorithm for SVM given in Hastie et al. (2004).

Let us consider a partition of the inliers in \(\mathcal {I}\) into the following three disjoint sets:

$$\begin{aligned} \mathcal {R}:= & {} \{ i | 1< y_i f({\varvec{x}}_i) \}, \\ \mathcal {E}:= & {} \{ i | y_i f({\varvec{x}}_i) = 1 \}, \\ \mathcal {L}:= & {} \{ i | s< y_i f({\varvec{x}}_i) < 1 \}. \end{aligned}$$

For a given fixed partition \(\{\mathcal {R}, \mathcal {E}, \mathcal {L}, \mathcal {O}\}\), the KKT conditions of the convex problem (8) indicate that

$$\begin{aligned} \alpha _i = 0 ~\forall ~ i \in \mathcal {R}, ~~ \alpha _i = C ~\forall ~ i \in \mathcal {L}, ~~ \alpha _i = C \theta ~\forall ~ i \in \mathcal {O}. \end{aligned}$$

The KKT conditions also imply that the remaining Lagrange multipliers \(\{\alpha _i\}_{i \in \mathcal {E}}\) must satisfy the following linear system of equations:

$$\begin{aligned} y_i f({\varvec{x}}_i)= & {} \sum _{j \in \mathbb {N}_n} \alpha _j y_i y_j K({\varvec{x}}_i, {\varvec{x}}_j) = 1 ~\forall ~ i \in \mathcal {E}\nonumber \\ \Leftrightarrow ~~ {\varvec{Q}}_{\mathcal {E}\mathcal {E}} {\varvec{\alpha }}_{\mathcal {E}}= & {} \mathbf {1}- {\varvec{Q}}_{\mathcal {E}\mathcal {L}} \mathbf {1}C - {\varvec{Q}}_{\mathcal {E}\mathcal {O}} \mathbf {1}C \theta , \end{aligned}$$
(19)

where \({\varvec{Q}} \in \mathbb {R}^{n \times n}\) is an \(n \times n\) matrix whose \((i, j)^\mathrm{th}\) entry is defined as \(Q_{ij} := y_i y_j K({\varvec{x}}_i, {\varvec{x}}_j)\). Here, a notation such as \({\varvec{Q}}_{\mathcal {E}\mathcal {L}}\) represents a submatrix of \({\varvec{Q}}\) having only the rows in the index set \(\mathcal {E}\) and the columns in the index set \(\mathcal {L}\). By solving the linear system of equations (19), the Lagrange multipliers \(\alpha _i, i \in \mathbb {N}_n\), can be written as an affine function of \(\theta \).

Noting that \(y_i f({\varvec{x}}_i) = \sum _{j \in \mathbb {N}_n} \alpha _j y_i y_j K({\varvec{x}}_i, {\varvec{x}}_j)\) is also represented as an affine function of \(\theta \), any changes of the partition \(\{\mathcal {R}, \mathcal {E}, \mathcal {L}\}\) can be exactly identified when the homotopy parameter \(\theta \) is continuously decreased. Since the solution path linearly changes for each partition of \(\{\mathcal {R}, \mathcal {E}, \mathcal {L}\}\), the entire path is represented as a continuous piecewise-linear function of the homotopy parameter \(\theta \). We denote the points in \(\theta \in [0, 1)\) at which members of the sets \(\{\mathcal {R}, \mathcal {E}, \mathcal {L}\}\) change as break-points \(\theta _{BP}\).

Using the piecewise-linearity of \(y_i f({\varvec{x}}_i)\), we can also identify when we should switch to the D-step. Once we detect an instance satisfying \(y_i f({\varvec{x}}_i) = s\), we exit the C-step and enter the D-step.

4.3 Continuous-step for OP-s

Since \(\theta \) is fixed to 0 in OP-s, the KKT conditions (10) yields

$$\begin{aligned} \alpha _i = 0 ~ \forall ~ i \in \mathcal {O}. \end{aligned}$$

This means that outliers have no influence on the solution and thus the conditionally optimal solution \(f^*_{\mathcal {P}}\) does not change with s as long as the partition \(\mathcal {P}\) is unchanged. The only task in the C-step for OP-s is therefore to find the next s that changes the partition \(\mathcal {P}\). Such s can be simply found as

$$\begin{aligned} s ~\leftarrow ~ \min _{i \in \mathcal {L}} y_i f({\varvec{x}}_i). \end{aligned}$$

4.4 Discontinuous-step (for both OP-\(\theta \) and OP-s)

As mentioned before, any convex QP solver can be used for the D-step. When the algorithm enters the D-step, we have the conditionally optimal solution \(f^*_\mathcal {P}\) for the partition \(\mathcal {P}:= \{\mathcal {I}, \mathcal {O}\}\). Our task here is to find another conditionally optimal solution \(f^*_{\tilde{\mathcal {P}}}\) for \(\tilde{\mathcal {P}} := \{\tilde{\mathcal {I}}, \tilde{\mathcal {O}}\}\) given by (11).

Given that the difference between the two solutions \(f^*_\mathcal {P}\) and \(f^*_{\tilde{\mathcal {P}}}\) is typically small, the D-step can be efficiently implemented by a technique used in the context of incremental learning (Cauwenberghs and Poggio 2001).

Let us define

$$\begin{aligned} \varDelta _{\mathcal {I}\rightarrow \mathcal {O}}&:= \{i \in \mathcal {I}~ | ~ y_i f_{\mathcal {P}}({\varvec{x}}_i) = s \}, \\ \varDelta _{\mathcal {O}\rightarrow \mathcal {I}}&:= \{i \in \mathcal {O}~ | ~ y_i f_{\mathcal {P}}({\varvec{x}}_i) = s \}. \end{aligned}$$

Then, we consider the following parameterized problem with parameter \(\mu \in [0, 1]\):

$$\begin{aligned} f_{\tilde{\mathcal {P}}}({\varvec{x}}_i; \mu ) := f_{\tilde{\mathcal {P}}}({\varvec{x}}_i) + \mu \varDelta f_i ~ \forall ~ i \in \mathbb {N}_n, \end{aligned}$$

where

$$\begin{aligned} \varDelta f_i := y_i \left[ \begin{array}{cc} {\varvec{K}}_{i, \varDelta _{\mathcal {I}\rightarrow \mathcal {O}}} &{} {\varvec{K}}_{i, \varDelta _{\mathcal {O}\rightarrow \mathcal {I}}} \\ \end{array}\right] \left[ \begin{array}{c} {\varvec{\alpha }}^\mathrm{(bef)}_{\varDelta _{\mathcal {I}\rightarrow \mathcal {O}}} - \mathbf {1}C \theta \\ {\varvec{\alpha }}^\mathrm{(bef)}_{\varDelta _{\mathcal {O}\rightarrow \mathcal {I}}} - \mathbf {1}C \end{array}\right] , \end{aligned}$$

and \({\varvec{\alpha }}^{(\mathrm bef)}\) be the corresponding \({\varvec{\alpha }}\) at the beginning of the D-Step. We can show that \(f_{\tilde{\mathcal {P}}}({\varvec{x}}_i; \mu )\) is reduced to \(f_{\mathcal {P}}({\varvec{x}}_i)\) when \(\mu = 1\), while it is reduced to \(f_{\tilde{\mathcal {P}}}({\varvec{x}}_i)\) when \(\mu = 0\) for all \(i \in \mathbb {N}_n\). By using a similar technique to incremental learning (Cauwenberghs and Poggio 2001), we can efficiently compute the path of solutions when \(\mu \) is continuously changed from 1 to 0. This algorithm behaves similarly to the C-step in OP-\(\theta \). The implementation detail of the D-step is described in Appendix 10.

5 Numerical experiments

In this section, we compare the proposed outlier-path (OP) algorithm with conventional concave-convex procedure (CCCP) (Yuille and Rangarajan 2002) because, in most of the existing robust SVM studies, non-convex optimization for robust SVM training are solved by CCCP or a variant called difference of convex (DC) programming (Shen et al. 2003; Krause and Singer 2004; Liu et al. 2005; Liu and Shen 2006; Collobert et al. 2006; Wu and Liu 2007).

5.1 Setup

We used several benchmark data sets listed in Tables 1 and 2. We randomly divided data set into training (40%), validation (30%), and test (30%) sets for the purposes of optimization, model selection (including the selection of \(\theta \) or s), and performance evaluation, respectively. For robust SVC, we randomly flipped 15, 20, 25% of the labels in the training and the validation data sets. For robust SVR, we first preprocess the input and output variables; each input variable was normalized so that the minimum and the maximum values are \(-1\) and \(+1\), respectively, while the output variable was standardized to have mean zero and variance one. Then, for the 5, 10, 15% of the training and the validation instances, we added an uniform noise \(U(-2, 2)\) to input variable, and a Gaussian noise \(N(0, 10^2)\) to output variable, where U(a, b) denotes the uniform distribution between a and b and \(N(\mu ,\sigma ^2)\) denotes the normal distribution with mean \(\mu \) and variance \(\sigma ^2\).

Table 1 Benchmark data sets for robust SVC experiments
Full size table
Table 2 Benchmark data sets for robust SVR experiments
Full size table
Table 3 The mean of test error by 0–1 loss and standard deviation (linear, robust SVC)
Full size table

5.2 Generalization performance

First, we compared the generalization performance. We used the linear kernel and the radial basis function (RBF) kernel defined as \(K({\varvec{x}}_i, {\varvec{x}}_j) = \exp \left( -\gamma \Vert {\varvec{x}}_i - {\varvec{x}}_j\Vert ^2 \right) \), where \(\gamma \) is a kernel parameter fixed to \(\gamma =1/d\) with d being the input dimensionality. Model selection was carried out by finding the best hyper-parameter combination that minimizes the validation error. We have a pair of hyper-parameters in each setup. In all the setups, the regularization parameter C was chosen from \(\{0.01, 0.1, 1, 10, 100\}\), while the candidates of the homotopy parameters were chosen as follows:

  • In OP-\(\theta \), the set of break-points \(\theta _{BP} \in [0,1]\) was considered as the candidates (note that the local solutions at each break-point have been already computed in the homotopy computation).

  • In OP-s, the set of break-points in \([s_C, 0]\) was used as the candidates for robust SVC, where

    $$\begin{aligned} s_C := \min _{i \in \mathbb {N}_n} y_i f_\mathrm{SVC}({\varvec{x}}_i) \end{aligned}$$

    with \(f_\mathrm{SVC}\) being the ordinary non-robust SVC. For robust SVR, the set of break-points in \([s_R, 0.2S_R]\) was used as the candidates, where

    $$\begin{aligned} s_R := \max _{i \in \mathbb {N}_n} |y_i - f_\mathrm{SVR}({\varvec{x}}_i)| \end{aligned}$$

    with \(f_\mathrm{SVC}\) being the ordinary non-robust SVR.

  • In CCCP-\(\theta \), the homotopy parameter \(\theta \) was selected from

    $$\begin{aligned} \theta \in \{1, 0.75, 0.5, 0.25, 0\}. \end{aligned}$$

  • In CCCP-s, the homotopy parameter s was selected from

    $$\begin{aligned} s \in \{s_C, 0.75s_C, 0.5s_C, 0.25s_C, 0\} \end{aligned}$$

    for robust SVC, while it was selected from

    $$\begin{aligned} s \in \{s_R, 0.8s_R, 0.6s_R, 0.4s_R, 0.2s_R\} \end{aligned}$$

    for robust SVR.

Note that both OP and CCCP were initialized by using the solution of standard SVM.

Fig. 7
figure 7

Elapsed time when the number of (\(\theta ,s\))-candidates is increased. Changing the number of hyper-parameter candidates affects the computation time of CCCP, but not OP because the entire path of solutions is computed with the infinitesimal resolution. a Elapsed time for CCCP and OP (linear, robust SVC). b Elapsed time for CCCP and OP (RBF, robust SVC). c Elapsed time for CCCP and OP (linear, robust SVR). d Elapsed time for CCCP and OP (RBF, robust SVR)

Full size image

Table 3 represents the average and the standard deviation of the test errors on 10 different random data splits. The other results on different noise levels summarized in Appendix 11. These results indicate that our proposed OP algorithm tends to find better local solutions and the degree of robustness was appropriately controlled. It seems that OP-s is the best one if we only use one of these methods.

Table 4 The mean of test error by 0–1 loss and standard deviation
Full size table

5.3 Computation time

Second, we compared the computational costs of the entire model-building process of each method. The results are shown in Fig. 7. Note that the computational cost of the OP algorithm does not depend on the number of hyper-parameter candidates of \(\theta \) or s, because the entire path of local solutions has already been computed with the infinitesimal resolution in the homotopy computation. On the other hand, the computational cost of CCCP depends on the number of hyper-parameter candidates. In our implementation of CCCP, we used the warm-start approach, i.e., we initialized CCCP with the previous solution for efficiently computing a sequence of solutions. The results indicate that the proposed OP algorithm enables stable and efficient control of robustness, while CCCP suffers a trade-off between model selection performance and computational costs.

Table 5 The mean of test error by 0–1 loss and standard deviation (linear, robust SVC)
Full size table

5.4 Stability of concave-convex procedure (CCCP)

Finally, we empirically investigate the stability of CCCP algorithm. For simplicity, we only considered a linear classification problem on BreastCancerDiagnostic data with the homotopy parameters \(\theta =0\) and \(s=0\). Remember that, \(\theta =1\) corresponds to the hinge loss function for the standard convex SVM, while \(\theta =0\) corresponds to fully robust ramp loss function. Here, we used warm-start approaches for obtaining a robust SVM solution for \(\theta = 0\) by considering a sequence of \(\theta \) values: \(\theta _{(\ell )} := 1 - \frac{\ell }{L}, \ell = 0, 1, \ldots , L\) (another homotopy parameter s was fixed to be 0). Specifically, we started from the standard convex SVM solution with \(\theta _{(0)} = 1\), and used it as a warm-start initial solution for \(\theta _{(1)}\), and used it as a warm-start initial solution for \(\theta _{(2)}\), and so on.

Table 4 shows the average and the standard deviation of the test errors on 30 different random data splits for the three warm-start approaches with \(L = 5, 10, 15\) (the performances of CCCP in Table 3 are the results with \(L=5\)). The results indicate that the performances (for \(\theta =0\)) were slightly better, i.e., better local optimal solutions were obtained when the length of the sequence L is larger. We conjecture that it is because the warm-start approach can be regarded as a simulated annealing, and the performances were better when the annealing step size (\(=1/L\)) is smaller.

It is important to note that, if we consider the above warm-start approach with very large L, we would be able to obtain similar results as the proposed homotopy approach. In other words, the proposed homotopy approach can be considered as an efficient method for conducting simulated annealing with infinitesimally small annealing step size. Table 5 shows the same results as Table 3 for three different CCCP approaches with \(L=5, 10, 15\). As we discussed above, the performances tend to be better when L is large, although the computational cost also increases when L gets large.

6 Conclusions

In this paper, we proposed a novel robust SVM learning algorithm based on the homotopy approach that allows efficient computation of the sequence of local optimal solutions when the influence of outliers is gradually decreased. The algorithm is built on our theoretical findings about the geometric property and the optimality conditions of local solutions of robust SVM. Experimental results indicate that our algorithm tends to find better local solutions possibly due to the simulated annealing-like effect and the stable control of robustness. One of the important future works is to adopt scalable homotopy algorithms (Zhou et al. 2012) or approximate parametric programming algorithms (Giesen et al. 2012) for further improving the computational efficiency.