Thermo-electro-mechanical size-dependent postbuckling response of axially loaded piezoelectric shear deformable nanoshells via nonlocal elasticity theory

Abstract

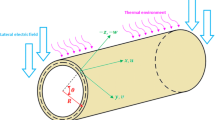
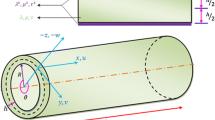
The current study addresses the size-dependent nonlinear thermo-electro-mechanical instability of piezoelectric nanoshells under a combined action of axial compressive load, lateral electric field and uniform changes in temperature. The non-classical formulations given herein are built upon the nonlocal elasticity theory within the framework of the shear deformation shell theory. On the basis of the minimum potential energy of the system and using a boundary layer theory of shell buckling, the nonlocal-based governing equations are deduced incorporating the nonlinear prebuckling deformations and initial geometric imperfection sensitivity. After that, a perturbation-based solution methodology is put to use in order to anticipate the size-dependent thermo-electro-mechanical postbuckling response of piezoelectric nanoshells corresponding to different nonlocal parameters, applied electric voltages and temperature changes. It is displayed that for the both local and nonlocal models with and without initial geometric imperfection, a lateral electric field coming from a positive applied voltage leads to increase the axial stiffness of piezoelectric nanoshell in such a way that the critical load and width of postbuckling domain increase, but no considerable change occurs in the minimum load of the postbuckling regime.

Appendices

Appendix A

The solutions in asymptotic forms corresponding to each of independent variables are extracted as below

$$ \begin{aligned} W & = {\mathcal{A}}_{00}^{\left( 0 \right)} + \epsilon \left[ {{\mathcal{A}}_{00}^{(1)} - {\mathcal{A}}_{00}^{(1)} \left( {\sin \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right) + \cos \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{\varGamma X}{\sqrt \epsilon }}} - {\mathcal{A}}_{00}^{(1)} \left( {\sin \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right) + \cos \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \hfill \\ & \quad + \epsilon^{2} \left[ {{\mathcal{A}}_{00}^{\left( 2 \right)} + {\mathcal{A}}_{11}^{\left( 2 \right)} \sin \left( {mX} \right)\sin \left( {nY} \right) + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right) - \left( {{\mathcal{A}}_{00}^{(2)} + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right)\left( {\sin \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right) + \cos \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{\varGamma X}{\sqrt \epsilon }}} - \left( {{\mathcal{A}}_{00}^{(2)} + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right)\left( {\sin \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right) + \cos \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \\ & \quad + \epsilon^{4} \left[ {{\mathcal{A}}_{00}^{\left( 4 \right)} + {\mathcal{A}}_{11}^{\left( 4 \right)} \sin \left( {mX} \right)\sin \left( {nY} \right) + {\mathcal{A}}_{20}^{\left( 4 \right)} \cos \left( {2mX} \right) + {\mathcal{A}}_{02}^{(4)} \cos (2nY) + {\mathcal{A}}_{13}^{(4)} \sin \left( {mX} \right)\sin \left( {3nY} \right) + {\mathcal{A}}_{22}^{(4)} \cos \left( {2mX} \right)\cos \left( {2nY} \right)} \right] + O\left( {\epsilon^{5} } \right), \\ \end{aligned} $$

(29)

$$ \begin{aligned} \varPsi_{X} & = \epsilon^{3/2} \left[ {{\mathcal{A}}_{00}^{(1)} c_{10}^{(3/2)} \sin \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right)e^{{ - \frac{\varGamma X}{\sqrt \epsilon }}} + {\mathcal{A}}_{00}^{(1)} c_{10}^{(3/2)} \sin \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)e^{{ - \frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \hfill \\ & \quad + \epsilon^{5/2} \left[ {\left( {{\mathcal{A}}_{00}^{(2)} + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right)c_{10}^{(5/2)} \sin \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right)e^{{ - \frac{\varGamma X}{\sqrt \epsilon }}} + \left( {{\mathcal{A}}_{00}^{(2)} + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right)c_{10}^{(5/2)} \sin \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)e^{{ - \frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \hfill \\ & \quad + \epsilon^{3} \left[ {{\mathcal{C}}_{11}^{\left( 3 \right)} \cos \left( {mX} \right){ \sin }\left( {nY} \right)} \right] + O\left( {\epsilon^{5} } \right), \hfill \\ \end{aligned} $$

(30)

(31)

$$ \varPsi_{Y} = \epsilon^{3} \left[ {{\mathcal{D}}_{11}^{(3)} \sin \left( {mX} \right){ \cos }(nY) + {\mathcal{D}}_{02}^{\left( 3 \right)} { \sin }(2nY)} \right] + O\left( {\epsilon^{5} } \right). $$

(32)

Appendix B

$$ {\mathcal{P}}_{x}^{\left( 0 \right)} = \frac{1}{2}\left\{ {K_{0} \epsilon^{ - 1} + K_{3} \beta^{2} \epsilon } \right\}, $$

(33)

$$ {\mathcal{P}}_{x}^{\left( 2 \right)} = - \frac{1}{2}\left\{ {\left( {\frac{{6n^{2} \beta^{2} K_{0}^{2} }}{{K_{2} }}} \right)\epsilon^{ - 1} - \left( {2K_{6} \beta^{2} n^{2} + \frac{{K_{0} K_{4} H_{20} \beta^{4} n^{4} + 4K_{0} K_{5} H_{20} \beta^{2} n^{2} }}{{2(K_{0} H_{20} - K_{4} )}} + \frac{{K_{0}^{2} H_{20} \beta^{4} n^{4} + 4K_{0} K_{5} \beta^{2} n^{2} }}{{2(K_{0} H_{20} - K_{4} )}} + \frac{{K_{0}^{2} \beta^{4} n^{4} + 4K_{0} K_{5} \beta^{2} n^{2} }}{{2(K_{0} - K_{4} )}}} \right)\epsilon } \right\} , $$

(34)

$$ {\mathcal{P}}_{x}^{\left( 4 \right)} = \frac{1}{2}\left\{ {\left( {\frac{{12K_{0}^{3} K_{7} H_{13} \beta^{2} n^{4} }}{{K_{2}^{2} \left( {K_{0} H_{13} - K_{7} } \right)}} + \frac{{4\beta^{2} n^{4} K_{0}^{3} \left( {K_{0} + 2K_{7} } \right)}}{{K_{2}^{2} \left( {K_{0} - K_{7} } \right)}} + \frac{{16\beta^{4} n^{4} K_{0}^{3} }}{{K_{2}^{2} }}} \right)\epsilon^{ - 1} } \right\} , $$

(35)

$$ \delta_{x}^{(0)} = \vartheta_{1} {\mathcal{P}}_{x} + \left( {\frac{{\alpha \vartheta_{2}^{2} {\mathcal{P}}_{x}^{2} }}{\pi } - \frac{{2\vartheta_{2}^{2} {\mathcal{P}}_{x} }}{{\pi \vartheta_{1} a}}} \right)\epsilon^{1/2} , $$

(36)

$$ \delta_{x}^{(2)} = \frac{{m^{2} \epsilon }}{16} , $$

(37)

$$ \delta_{x}^{(4)} = \frac{{\alpha K_{0}^{2} \epsilon^{ - 3/2} }}{{8\pi^{2} K_{2}^{2} }} + \frac{{m^{2} }}{4}\left( {\frac{{K_{0} H_{20} \beta^{2} n^{2} + 4K_{5} }}{{4\left( {K_{0} H_{20} - K_{4} } \right)}}} \right)^{2} \epsilon^{3} , $$

(38)

$$ \delta_{x}^{E} = \frac{{d_{31} R{\mathcal{V}}}}{{2h^{2} }}, $$

(39)

$$ \delta_{x}^{T} = \frac{\alpha R\Delta T}{2h}, $$

(40)

where

$$ H_{11} = 1 + \pi^{2} {\mathcal{G}}^{2} \left( {m^{2} + \beta^{2} n^{2} } \right) , \quad H_{02} = 1 + 4\pi^{2} {\mathcal{G}}^{2} \beta^{2} n^{2} , $$

$$ H_{20} = 1 + 4\pi^{2} {\mathcal{G}}^{2} m^{2} , \quad H_{13} = 1 + \pi^{2} {\mathcal{G}}^{2} \left( {m^{2} + 9\beta^{2} n^{2} } \right), $$

(41)

where $K_{i} (i = 0, \ldots ,7)$ are constant parameters extracted via the perturbation sets of equations.

$$ {\mathcal{S}}_{1} = - \frac{{K_{0} }}{{K_{2} }}\epsilon^{ - 1} + \left( {\frac{{a_{12}^{*} }}{{\left( {a_{11}^{*} } \right)^{2} - \left( {a_{12}^{*} } \right)^{2} }}} \right)\left( {2{\mathcal{P}}_{x}^{\left( 2 \right)} } \right), $$

(42)

$$ {\mathcal{S}}_{2} = \left( {\frac{{a_{12}^{*} }}{{\left( {a_{11}^{*} } \right)^{2} - \left( {a_{12}^{*} } \right)^{2} }}} \right)\left( {2{\mathcal{P}}_{x}^{\left( 0 \right)} } \right) + \frac{{d_{31} R{\mathcal{V}}}}{{h^{2} }} + \frac{\alpha R\Delta T}{h}. $$

(43)