Model order reduction for dynamic simulation of slender beams undergoing large rotations

Abstract

In this paper a model order reduction technique for the dynamic simulation of beams undergoing large rotations is presented. The finite element model for the motion of such beams is based on the corotational formulation. The trajectory piecewise linear model order reduction (TPWLMOR) method with second order Krylov subspace is used to obtain the reduced order model from the finite element model. Improvements are suggested to improve the accuracy and the computational efficiency of the TPWLMOR model. Several numerical examples which include forced undamped and damped beams are presented to validate the proposed method.

Appendix: Calculation of internal force vector and the inertia term

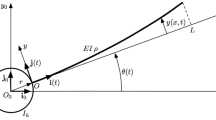
The equations of motion of a beam undergoing large rotations are derived using the corotational approach. The corotating beam element (see Fig. 1) in local coordinate is based on the Euler Bernoulli beam theory. Linear interpolation is used for axial displacement (u) while a cubic interpolation is used for transverse displacement (w). Thus the axial displacement, the transverse displacement and the rotation can be approximated as

$$\begin{aligned} u= & {} \frac{x}{L}\bar{u} \end{aligned}$$

(35)

$$\begin{aligned} w= & {} x\bigg (1-\frac{x}{L}\bigg )^2{\bar{\theta _{1}}}+\bigg (\frac{x^3}{L^2}-\frac{x^2}{L}\bigg ){\bar{\theta _{2}}} \end{aligned}$$

(36)

$$\begin{aligned} \theta= & {} \bigg (\frac{3x^2}{L^2}-\frac{4x}{L}+1\bigg ){\bar{\theta _{1}}}+\bigg (\frac{3x^2}{L^2}-\frac{2x}{L}\bigg ){\bar{\theta _{2}}} \end{aligned}$$

(37)

where $\bar{u}$ is the local axial displacement and ${\bar{\theta _{1}}}$ and ${\bar{\theta _{2}}}$ are the local rotations at nodes 1 and 2. The derivation of the internal force term and the inertia term in the equation of motion is given next.

1.1 Calculation of the internal force vector

The internal force vector is derived following Crisfield’s approach [14] which is based on the principle of virtual work. Using the above approximations for the local beam, the local axial force (N), and end moments $M_1$ and $M_2$ can be derived as follows [14],

$$\begin{aligned}&N=\frac{EA\bar{u}}{L} \end{aligned}$$

(38)

$$\begin{aligned}&\begin{bmatrix} M_1\\ M_2 \end{bmatrix} = \frac{EI}{L} \begin{bmatrix} 4&2\\ 2&4 \end{bmatrix} \begin{bmatrix} {\bar{\theta _{1}}}\\ {\bar{\theta _{2}}} \end{bmatrix} \end{aligned}$$

(39)

Note that the local internal force vector $\bar{\mathbf{f }}_I^{e}$ is given by,

$$\begin{aligned} \bar{\mathbf{f }}_I= [N \,\,\, M_1\,\,\, M_2]^T \end{aligned}$$

(40)

The local tangent stiffness, $\mathbf{K}_{l}$, can be obtained by relating the local internal forces vector, ${\bar{\mathbf{f}}}^{e}_{l}$, with local displacement vector, $\bar{\mathbf{q}}^{e}$, and is given by,

$$\begin{aligned} \mathbf{K}_{l}=\left[ \begin{array}{c@{\quad }c@{\quad }c} EA/L&{}0&{}0\\ 0&{}4EI/L&{}2EI/L\\ 0&{}2EI/L&{}4EI/L \end{array}\right] \end{aligned}$$

The global internal force vector ($\mathbf f _I^{e}$) can be related to the local internal force vector by

$$\begin{aligned} \mathbf f _I^{e}=\mathbf B ^T\bar{\mathbf{f }}^{e} \end{aligned}$$

(41)

where, $\mathbf B$ is a transformation matrix given by,

$$\begin{aligned} \mathbf B = \begin{bmatrix} \mathbf b _1\\ \mathbf b _2\\ \mathbf b _3 \end{bmatrix}= \begin{bmatrix} -c&-s&\quad 0&\quad c&\quad s&\quad 0\\ -s/L_n&\quad c/L_n&\quad 1&\quad s/L_n&\quad -c/L_n&\quad 0\\ -s/L_n&\quad c/L_n&\quad 0&\quad s/L_n&\quad -c/L_n&\quad 1 \end{bmatrix} \end{aligned}$$

(42)

Here $c=\cos (\beta )$, $s=\sin (\beta )$ and $L_n$ is the new length. and $\mathbf z =[s\,\,\, -c\,\,\,\,\, 0\,\,\, -s\,\,\,\,\, c\,\,\,\,\, 0]^T$

1.2 Calculation of inertia force vector

The inertia force vector is obtained using Le’s approach [25] and is based on using the expression of the kinetic energy of the beam element. In terms of the kinetic energy, the inertia force vector is given by [25],

$$\begin{aligned} \mathbf f _k^e=\frac{d}{dt}\bigg [\frac{\partial K^e}{\partial \dot{\mathbf{q ^e}} }\bigg ]-\bigg [\frac{\partial K^e}{\partial \mathbf q ^e}\bigg ] \end{aligned}$$

(43)

where, $K^e$ is the kinetic energy of the beam element. The expression for the kinetic energy in terms of a global nodal velocity vector $\dot{\mathbf{q ^e}}$ can be written in the form of,

$$\begin{aligned} K^e=\frac{1}{2}\dot{\mathbf{q ^e}}^T\mathbf M ^e\dot{\mathbf{q ^e}} \end{aligned}$$

(44)

where, $\dot{\mathbf{q ^e}}=[\dot{u}_1 \,\,\, \dot{w}_1 \,\,\, \dot{\theta }_1\,\,\, \dot{u}_2 \,\,\, \dot{w}_2 \,\,\, \dot{\theta }_2]^T$ is a global nodal velocity vector and $\mathbf M ^e$ is an elemental mass matrix in reference configuration. The elemental mass matrix in reference configuration is related to elemental mass matrix in local configuration $\mathbf M _l^e$ as,

$$\begin{aligned} \mathbf M ^e=\mathbf{T ^e}^T\mathbf M _l^e\mathbf T ^e \end{aligned}$$

(45)

where, $\mathbf T ^e$ is a transformation matrix and given by,

$$\begin{aligned} \mathbf T ^e= \begin{bmatrix} c&\quad s&\quad 0&\quad 0&\quad 0&\quad 0\\ -s&\quad c&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 1&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad c&\quad s&\quad 0\\ 0&\quad 0&\quad 0&\quad -s&\quad c&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 1 \end{bmatrix} \end{aligned}$$

(46)

Now the local mass matrix $\mathbf M _l^e$ is derived by making two assumptions. (i) local transverse displacement w is very small (ii) The new length of the beam element is approximately equal to the original length of the beam element. The local mass matrix $\mathbf M _l^e$ is then be written as,

$$\begin{aligned} \mathbf M _l^e=\mathbf{M _l^e}^1+\mathbf{M _l^e}^2 \end{aligned}$$

(47)

where, $\mathbf{M _l^e}^1$ is the local mass matrix for axial and transverse displacement and $\mathbf{M _l^e}^2$ is the local mass matrix for rotation. $\mathbf{M _l^e}^1$ and $\mathbf{M _l^e}^2$ are given by,

$$\begin{aligned}&\mathbf{M _l^e}^1=\frac{\rho A L}{420} \begin{bmatrix} 140&(21{\bar{\theta _{1}}}-14{\bar{\theta _{2}}})&0&70&-(21{\bar{\theta _{1}}}-14{\bar{\theta _{2}}})&0\\ (21{\bar{\theta _{1}}}-14{\bar{\theta _{2}}})&156&22L&(14{\bar{\theta _{1}}}-21{\bar{\theta _{2}}})&54&-13L\\ 0&22L&4L^2&0&13L&-3L^2 \\ 70&(14{\bar{\theta _{1}}}-21{\bar{\theta _{2}}})&0&140&-(14{\bar{\theta _{1}}}-21{\bar{\theta _{2}}})&0\\ -(21{\bar{\theta _{1}}}-14{\bar{\theta _{2}}})&54&13L&(14{\bar{\theta _{1}}}-21{\bar{\theta _{2}}})&156&-22L\\ 0&-13L&-3L^2&0&22L&4L^2 \end{bmatrix} \end{aligned}$$

(48)

$$\begin{aligned}&\mathbf{M _l^e}^2=\frac{\rho I}{30L} \begin{bmatrix} 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 36&\quad 3L&\quad 0&\quad -36&\quad 3L\\ 0&\quad 3L&\quad 4L^2&\quad 0&\quad -3L&\quad -L^2 \\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad -36&\quad -3L&\quad 0&\quad 36&\quad -3L\\ 0&\quad 3L&\quad -L^2&\quad 0&\quad -3L&\quad 4L^2 \end{bmatrix} \end{aligned}$$

(49)

The expressions for the two terms of Eq. (43) are given next.

1.2.1 Calculation of the first term of Eq. (43)

The first term of Eq. (43) can be written as

$$\begin{aligned} \frac{d}{dt}\bigg [\frac{\partial K^e}{\partial \dot{\mathbf{q }}^e}\bigg ]=\mathbf M ^e\ddot{\mathbf{q ^e}}+\dot{\mathbf{M ^e}}\dot{\mathbf{q ^e}} \end{aligned}$$

(50)

Note that $\mathbf M ^e$ is a function of $\beta$, ${\bar{\theta _{1}}}$ and ${\bar{\theta _{2}}}$ which are time dependent. The expression for $\dot{\mathbf{M }}^e$ is given by

$$\begin{aligned} \dot{\mathbf{M }}^e=\mathbf M _{\beta }^e\dot{\beta }+\mathbf M _{{\bar{\theta _{1}}}}^e\dot{{\bar{\theta _{1}}}}+\mathbf M _{{\bar{\theta _{2}}}}^e\dot{{\bar{\theta _{2}}}} \end{aligned}$$

(51)

where

$$\begin{aligned} \mathbf M _{\beta }^e=\frac{\partial \mathbf M ^e}{\partial \beta },\;\;\; \mathbf M _{{\bar{\theta _{1}}}}^e= \frac{\partial \mathbf M ^e}{\partial {\bar{\theta _{1}}}}\;\;\; \text{ and }\;\;\; \mathbf M _{{\bar{\theta _{2}}}}^e=\frac{\partial \mathbf M ^e}{\partial {\bar{\theta _{2}}}} \end{aligned}$$

Equation (51) can be rewritten as,

$$\begin{aligned} {\dot{\mathbf{M }}}^e=\mathbf{M }_{\beta }^e\bigg (\frac{\mathbf{z }^T}{L_n}\bigg ){\dot{\mathbf{q }}}^e +\mathbf{M }_{{\bar{\theta _{1}}}}^e(\mathbf{b }_2^T{\dot{\mathbf{q }}}^e) +\mathbf{M }_{{\bar{\theta _{2}}}}^e(\mathbf{b }_3^T{\dot{\mathbf{q }}}^e) \end{aligned}$$

(52)

Therefore, Eq. (50) can be written as,

$$\begin{aligned}&\frac{d}{dt}\bigg [\frac{\partial K^e}{\partial {\dot{\mathbf{q }}}^e}\bigg ]=\mathbf{M }^e{\ddot{\mathbf{q }}}^e +\bigg [\mathbf{M }_{\beta }^e\bigg (\frac{\mathbf{z }^T}{L_n}\bigg ){\dot{\mathbf{q }}}^e\nonumber \\&\quad +\,\mathbf{M }_{{\bar{\theta _{1}}}}^e(\mathbf{b }_2^T {\dot{\mathbf{q }}}^e)+\mathbf{M }_{{\bar{\theta _{2}}}}^e(\mathbf{b }_3^T{\dot{\mathbf{q }}}^e)\bigg ] {\dot{\mathbf{q }}}^e \end{aligned}$$

(53)

The expression for $\mathbf M _{\beta }^e$ can be obtained by differentiating Eq. (45) with respect to $\beta$

$$\begin{aligned} \mathbf M _{\beta }^e=\frac{d\mathbf{T ^e}^T}{d\beta }{} \mathbf M _l^e\mathbf T ^e+\mathbf{T ^e}^T\mathbf M _l^e\frac{d\mathbf T ^e}{d\beta } \end{aligned}$$

(54)

where,

$$\begin{aligned} \frac{d\mathbf T ^e}{d\beta }= \begin{bmatrix} 0&\quad 1&\quad 0&\quad 0&\quad 0&\quad 0\\ -1&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad 0&\quad 1&\quad 0\\ 0&\quad 0&\quad 0&\quad -1&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{bmatrix}{} \mathbf T ^e=\mathbf I _1^e\mathbf T ^e \end{aligned}$$

(55)

Therefore Eq. (54) can be written as,

$$\begin{aligned} \mathbf M _{\beta }^e=\mathbf{T ^e}^T(\mathbf I _1^e\mathbf M _l^e+\mathbf M _l^e\mathbf I _1^e)\mathbf T ^e \end{aligned}$$

(56)

Similarly, expressions for $\mathbf M _{{\bar{\theta _{1}}}}^e$ and $\mathbf M _{{\bar{\theta _{2}}}}^e$ are given by,

$$\begin{aligned} \mathbf M _{{\bar{\theta _{1}}}}^e= & {} \mathbf{T ^e}^T\frac{\partial \mathbf M _l^e}{\partial {\bar{\theta _{1}}}}{} \mathbf T ^e \end{aligned}$$

(57)

$$\begin{aligned} \mathbf M _{{\bar{\theta _{2}}}}^e= & {} \mathbf{T ^e}^T\frac{\partial \mathbf M _l^e}{\partial {\bar{\theta _{2}}}}{} \mathbf T ^e \end{aligned}$$

(58)

where,

$$\begin{aligned} \frac{\partial \mathbf M _l^e}{\partial {\bar{\theta _{1}}}}= & {} \frac{\rho A L}{60} \begin{bmatrix} 0&\quad 3&\quad 0&\quad 0&\quad -3&\quad 0\\ 3&\quad 0&\quad 0&\quad 2&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad 2&\quad 0&\quad 0&\quad -2&\quad 0\\ -3&\quad 0&\quad 0&\quad -2&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{bmatrix} \end{aligned}$$

(59)

$$\begin{aligned} \frac{\partial \mathbf M _l^e}{\partial {\bar{\theta _{2}}}}= & {} \frac{\rho A L}{60} \begin{bmatrix} 0&\quad -2&\quad 0&\quad 0&\quad 2&\quad 0\\ -2 \quad&0&\quad 0&\quad -3&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad -3&\quad 0&\quad 0&\quad 3&\quad 0\\ 2&\quad 0&\quad 0&\quad 3&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{bmatrix} \end{aligned}$$

(60)

1.2.2 Calculation of second term of Eq. (43)

The second term of Eq. (43) is given by

$$\begin{aligned} \frac{\partial K^e}{\partial \mathbf q ^e}= & {} \frac{\partial K^e}{\partial \beta } \frac{\partial \beta }{\partial \mathbf q ^e} +\frac{\partial K^e}{\partial {\bar{\theta _{1}}}} \frac{\partial {\bar{\theta _{1}}}}{\partial \mathbf q ^e} +\frac{\partial K^e}{\partial {\bar{\theta _{2}}}} \frac{\partial {\bar{\theta _{2}}}}{\partial \mathbf q ^e} \nonumber \\= & {} \bigg (\frac{1}{2}\dot{\mathbf{q }}^{eT}{} \mathbf M _{\beta }^e\dot{\mathbf{q }}^e \bigg ) \frac{\partial \beta }{\partial \mathbf q ^e}\nonumber \\&+\, \bigg (\frac{1}{2}\dot{\mathbf{q }}^{eT}{} \mathbf M _{{\bar{\theta _{1}}}}^e\dot{\mathbf{q }}^e\bigg ) \frac{\partial {\bar{\theta _{1}}}}{\partial \mathbf q ^e} +\bigg (\frac{1}{2}\dot{\mathbf{q }}^{eT}{} \mathbf M _{{\bar{\theta _{2}}}}^e\dot{\mathbf{q }}^e\bigg ) \frac{\partial {\bar{\theta _{2}}}}{\partial \mathbf q ^e} \end{aligned}$$

(61)

Equation (61) can be rewritten as,

$$\begin{aligned} \frac{\partial K^e}{\partial \mathbf{q }^e}=\bigg (\frac{1}{2}{\dot{\mathbf{q }}}^{eT}\mathbf{M }_{\beta }^e{\dot{\mathbf{q }}}^e\bigg ) \frac{\mathbf{z }}{L_n} +\bigg (\frac{1}{2}{\dot{\mathbf{q }}}^{eT}\mathbf{M }_{{\bar{\theta _{1}}}}^e{\dot{\mathbf{q }}}^e\bigg ) \mathbf{b }_2 +\bigg (\frac{1}{2}{\dot{\mathbf{q }}}^{eT}\mathbf{M }_{{\bar{\theta _{2}}}}^e{\dot{\mathbf{q }}}^e\bigg ) \mathbf{b }_3 \end{aligned}$$

(62)

Now the inertia force term can be obtained by substituting Eqs. (53) and (62) in Eq. (43),

$$\begin{aligned} \mathbf{f }_k^e= & {} \mathbf{M }^e{\ddot{\mathbf{q }}}^e +\left[ \mathbf{M }_{\beta }^e \bigg (\frac{\mathbf{z }^T}{L_n}\bigg ){\dot{\mathbf{q }}}^e +\mathbf{M }_{{\bar{\theta _{1}}}}^e(\mathbf{b }_2^T {\dot{\mathbf{q }}}^e)+\mathbf{M }_{{\bar{\theta _{2}}}}^e(\mathbf{b }_3^T {\dot{\mathbf{q }}}^e)\right] {\dot{\mathbf{q }}}^e\nonumber \\&-\,\left[ \bigg (\frac{1}{2} {\dot{\mathbf{q }}}^{eT}\mathbf{M }_{\beta }^e{\dot{\mathbf{q }}}^e\bigg ) \frac{\mathbf{z }}{L_n}+\bigg (\frac{1}{2}{\dot{\mathbf{q }}}^{eT} \mathbf{M }_{{\bar{\theta _{1}}}}^e{\dot{\mathbf{q }}}^e\bigg ) \mathbf{b }_2 \,+\,\bigg (\frac{1}{2}{\dot{\mathbf{q }}}^{eT} \mathbf{M }_{{\bar{\theta _{2}}}}^e{\dot{\mathbf{q }}}^e\bigg ) \mathbf{b }_3 \right] \nonumber \\ \end{aligned}$$

(63)