2D Fourier series representation of gravitational functionals in spherical coordinates

Abstract

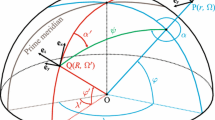
2D Fourier series representation of a scalar field like gravitational potential is conventionally derived by making use of the Fourier series of the Legendre functions in the spherical harmonic representation. This representation has been employed so far only in the case of a scalar field or the functionals that are related to it through a radial derivative. This paper provides a unified scheme to represent any gravitational functional in terms of spherical coordinates using a 2D Fourier series representation. The 2D Fourier series representation for each individual point is derived by transforming the spherical harmonics from the geocentric Earth-fixed frame to a rotated frame so that its equator coincides with the local meridian plane of that point. In the obtained formulation, each functional is linked to the potential in the spectral domain using a spectral transfer. We provide the spectral transfers of the first-, second- and third-order gradients of the gravitational potential in the local north-oriented reference frame and also those of some functionals of frequent use in the physical geodesy. The obtained representation is verified numerically. Moreover, spherical harmonic analysis of anisotropic functionals and contribution analysis of the third-order gradient tensor are provided as two numerical examples to show the power of the formulation. In conclusion, the 2D Fourier series representation on the sphere is generalized to functionals of the potential. In addition, the set of the spectral transfers can be considered as a pocket guide that provides the spectral characteristics of the functionals. Therefore, it extends the so-called Meissl scheme.

Appendix

The differential operators of the first- to third-order gradients are given in the following. Employing these operators and making use of the Laplace equation and its derivatives in the spectral domain results in the corresponding spectral transfers.

• First-order gradients

  $$\begin{aligned} D_{x}= & {} \frac{1}{r}\partial {_\phi }, \end{aligned}$$

  (20)
  $$\begin{aligned} D_{y}= & {} \frac{1}{r}\partial {_{\phi '}}, \end{aligned}$$

  (21)
  $$\begin{aligned} D_{z}= & {} \frac{1}{r}\partial {_r}. \end{aligned}$$

  (22)

• Second-order gradients

  $$\begin{aligned} D_{xx}= & {} \frac{1}{r^2}\partial {_{\phi \phi }}+\frac{1}{r}\partial {_r}, \end{aligned}$$

  (23)
  $$\begin{aligned} D_{xy}= & {} \frac{1}{r^2}\partial {_{\phi {\phi '}}}, \end{aligned}$$

  (24)
  $$\begin{aligned} D_{xz}= & {} \frac{1}{r}\partial {_{r\phi }}-\frac{1}{r^2}\partial {_{\phi }}, \end{aligned}$$

  (25)
  $$\begin{aligned} D_{yy}= & {} \frac{1}{r^2}\partial {_{{\phi '}{\phi '}}}+\frac{1}{r}\partial {_r}, \end{aligned}$$

  (26)
  $$\begin{aligned} D_{yz}= & {} \frac{1}{r}\partial {_{r{\phi '}}}-\frac{1}{r^2}\partial {_{\phi '}}, \end{aligned}$$

  (27)
  $$\begin{aligned} D_{zz}= & {} \partial {_{rr}}. \end{aligned}$$

  (28)

• Third-order gradients

  $$\begin{aligned} D_{xxx}= & {} \frac{1}{r^3}\partial {_{\phi \phi \phi }}+\frac{3}{r^2}\partial {_{r\phi }}- \frac{2}{r^3}\partial {_\phi }, \end{aligned}$$

  (29)
  $$\begin{aligned} D_{xxy}= & {} \frac{1}{r^2}\partial {_{r{\phi '}}}+\frac{1}{r^3} \partial {{\phi \phi {\phi '}}}, \end{aligned}$$

  (30)
  $$\begin{aligned} D_{xxz}= & {} \frac{1}{r}\partial {_{rr}}+\frac{1}{r^2}\partial {_{r\phi \phi }}- \frac{1}{r^2}\partial {_r}-\frac{2}{r^3}\partial {_{\phi \phi }}, \end{aligned}$$

  (31)
  $$\begin{aligned} D_{xyy}= & {} \frac{1}{r^2}\partial {_{r\phi }}+\frac{1}{r^3} \partial {_{\phi {\phi '}{\phi '}}}- \frac{1}{r^3}\partial {_\phi }, \end{aligned}$$

  (32)
  $$\begin{aligned} D_{xyz}= & {} \frac{1}{r^2}\partial {_{r\phi {\phi '}}}-\frac{2}{r^3} \partial {_{\phi {\phi '}}}, \end{aligned}$$

  (33)
  $$\begin{aligned} D_{xzz}= & {} \frac{1}{r}\partial {_{rr\phi }}-\frac{2}{r^2}\partial {_{r\phi }}+ \frac{2}{r^3}\partial {_\phi }, \end{aligned}$$

  (34)
  $$\begin{aligned} D_{yyy}= & {} \frac{3}{r^2}\partial {_{r{\phi '}}}+\frac{1}{r^3} \partial {_{{\phi '}{\phi '}{\phi '}}}-\frac{2}{r^3}\partial {_{\phi '}}, \end{aligned}$$

  (35)
  $$\begin{aligned} D_{yyz}= & {} \frac{1}{r}\partial {_{rr}}-\frac{1}{r^2} \partial {_r}+\frac{1}{r^2}\partial {_{r{\phi '}{\phi '}}}- \frac{2}{r^3}\partial {_{{\phi '}{\phi '}}}, \end{aligned}$$

  (36)
  $$\begin{aligned} D_{yzz}= & {} \frac{1}{r}\partial {_{rr{\phi '}}}-\frac{2}{r^2} \partial {_{r{\phi '}}}+\frac{2}{r^3}\partial {_{\phi '}}, \end{aligned}$$

  (37)
  $$\begin{aligned} D_{zzz}= & {} \partial {_{rrr}} \end{aligned}$$

  (38)