RGA: a unified measure of predictive accuracy

Abstract

A key point to assess statistical forecasts is the evaluation of their predictive accuracy. Recently, a new measure, called Rank Graduation Accuracy (RGA), based on the concordance between the ranks of the predicted values and the ranks of the actual values of a series of observations to be forecast, was proposed for the assessment of the quality of the predictions. In this paper, we demonstrate that, in a classification perspective, when the response to be predicted is binary, the RGA coincides both with the AUROC and the Wilcoxon-Mann–Whitney statistic, and can be employed to evaluate the accuracy of probability forecasts. When the response to be predicted is real valued, the RGA can still be applied, differently from the AUROC, and similarly to measures such as the RMSE. Differently from the RMSE, the RGA measure evaluates point predictions in terms of their ranks, rather than in terms of their values, improving robustness.

1 Background and motivation

One of the most important challenges for statistical learning methods is the construction of predictive accuracy tools that can evaluate and monitor the quality of the forecasts. For a review, see for example Hand and Till (2011), Gneiting (2011), Kang et al. (2021), Petropoulos et al. (2022) and the references therein. In this context, we aim to generalise the AUROC measure, in line with recent extensions provided by Hand and Till (2011) and Hand and Anagnostopoulos (2023), who proposed and discussed the H measure; and by Vivo et al. (2018), who proposed a partial area under the ROC curve (pAUC), to deal with the case of crossing ROC curves. In parallel to these developments, the increasing availability of computational power has allowed the implementation of predictive accuracy measures in several contexts and to compare, on the same data, different types of machine learning models. The traditional paradigm compares machine learning models within a model selection procedure, in which a model is chosen through a sequence of pairwise comparisons, based on the comparison of the likelihoods (or of the posterior probabilities) of the models being compared. These criteria are not generally applicable, when an underlying probabilistic model is not specified, as in neural networks and random forest models.

These considerations suggest that classical model comparison is not sufficient to compare the models that can be learned from the data. Indeed, the last few years have witnessed the growing importance of model comparison methods based on the comparison between the predicted and the actually observed cases, typically within cross-validation methods. In cross-validation, the data is split in two datasets, with a “training” dataset used to fit a model and a “validation” dataset used to compare the predictions made by the fitted model with the actual observed values.

The predictive accuracy of a model can be assessed through some specific metrics, of which use depends on the nature of the target variable to be predicted. When the response variable is continuous, the root mean square error (RMSE) is the most employed measure. The RMSE, related to the Pearson’s correlation coefficient, is based on the Euclidean distance between the predictions and the actual values. In the case of an ordinal response variable, the predicted and actual values can be replaced with their ranks, leading to the Spearman’s correlation coefficient and to Kendall’s $\tau$. When the target variable is binary, predictive accuracy can be evaluated through the Brier score (BS) which, similarly to the RMSE and the Spearman’s correlation coefficient, employs an Euclidean distance, calculated between the estimated probability for an event, and the observed outcomes (see Brier 1950). Alternatively to the BS, predictive accuracy can be evaluated in terms of distance between predicted and actual probability forecasts of both 0 and 1 values, giving rise, when different cut-off thresholds are considered, to the AUROC as a main summary measure. While RMSE and BS generate metrics which allow to reach the condition of scale precision, Spearman’s coefficient and AUROC provide metrics which depend on the ranks and on the percentages of true and false predictions, missing the condition of scale precision.

Note that all previous accuracy measures depend on the type of response variable, and none of them can be universally applied. This can be a problem in automated Artificial Intelligence (AI) applications, where statistics is becoming a valuable asset for their theoretical and practical understanding, as discussed in the most recent contributions by Friedrich et al. (2022) and Vojíř and Kliegr (2020). In Friedrich et al. (2022), statistics is presented as an interdisciplinary scientific field which plays a pivotal role for the evaluation of the predictive accuracy of AI methods. In Vojíř and Kliegr (2020), the focus is on the quantification of the explainability of highly complex machine learning models through the proposal of a new framework for the interpretability of rule-based models. These works witness that statistics can play an important role in assessing the “Trustworthiness” of Artificial Intelligence, defined in recently proposed regulations, such as the EU AI Act (artificialintelligenceact.eu). In particular, statistics can be very helpful to assess four key S.A.F.E. principles: “Sustainability” (in terms of resilience to extreme events and cyber attacks), “Accuracy” (in terms of accurate predictions), “Fairness” (in terms of no-discrimination with respect to sub-groups of the population) and “Explainability” (in terms of human oversight of the results).

In this paper we will focus on the accuracy principle, to further deepening and extending the RGA measure introduced by Raffinetti (2023) as a “universal” metric, independent on the nature of the response variable. In line with the accuracy assessment perspective, we aim at showing the RGA capability not only to detect the best set of predictors to be selected, but also to detect the type of response variable which is more predictable and, therefore, more reliable. To better clarify our purpose, suppose we would like to build an Artificial Intelligence tool which, on the basis of all available data, suggests daily whether a local government should impose mobility restrictions in a region, due to the outburst of a pandemic (such as Covid-19). A natural response variable is the count of new daily infected cases. To decide what to do tomorrow the government could rely on the prediction of tomorrow’s count, and evaluate the reliability of the tool monitoring the RMSE of the predictions over time. But the government can also decide to rely on the prediction of whether tomorrow the count is above a certain threshold of incidence, and evaluate the reliability of the tool using the AUROC measure. How can a government decide which response to predict? It would be desirable if the AI itself solves this problem. Comparing the p-values is not a solution, as they depend on two different models. It is then necessary to consider a more general predictive accuracy measure that is model agnostic not only with respect to the type of model - function of the explanatory variables - to employ, but also with respect to the type of response variable to be predicted.

More formally, let Y be a response variable to be predicted through a (supervised) statistical learning model $f({\varvec{X}})$, where ${\varvec{X}}$ is a vector of h explanatory variables: $X_1,X_2,\ldots ,X_{h}$. The prurpose is to compare different models, in terms of predictive accuracy. To this aim we now introduce a framework, based on the notion of concordance, that generalises the predictive accuracy problem to all ordered variable scales: continuous, ordinal and binary.

Let D be the available data, a matrix with $h+1$ columns, corresponding to h explanatory variables and a response variable; and $N=n^{*}+n$ rows, corresponding to all the joint observations of Y and $X_1,X_2,\ldots ,X_{h}$, partitioned into a training set $D_{train}$, of dimension $n^{*}\times (h+1)$, from which the unknown parameters of a machine learning model can be estimated; and a test set $D_{test}$, of dimension $n\times (h+1)$, which can be used to obtain the n-dimensional vector ${\hat{y}}$ of the predicted values whose distance from the n observed values y will measure the predictive accuracy of the model.

When the Y variable is at least ordinal (continuous, ordered categorical or binary), the Y values can be used to build the Lorenz curve (see e.g. Lorenz 1905), $L_Y$, arranging the Y values in a non-decreasing sense. More formally, for $i=1,\ldots ,n$, the Lorenz curve is defined by the pair: $(i/n,\sum _{j=1}^{i}y_{r_{j}}/(n{\bar{y}}))$, where $r_{j}$ indicates the non-decreasing ranks of Y and ${\bar{y}}$ indicates the mean of Y.

The same Y values can also be used to build the dual Lorenz curve, $L^{'}_{Y}$, ordering the Y values in a non-increasing sense. More formally, for $i=1,\ldots ,n$, the dual Lorenz curve is defined by the pair: $(i/n,\sum _{j=1}^{i}y_{r_{n+1-j}}/(n{\bar{y}}))$, where $r_{n+1-j}$ indicates the non-increasing ranks of Y.

A similar reasoning can be employed to order the predicted values ${\hat{Y}}$. Let ${\hat{r}}_i$, for $i=1,\ldots ,n$, indicate the non-decreasing ranks of ${\hat{Y}}$. Giudici and Raffinetti (2011) suggested to build a concordance curve C by ordering the Y values not in terms of their ranks, but with respect to ${\hat{r}}_i$, the ranks of the predicted ${\hat{Y}}$ values. Formally, for $i=1,\ldots ,n$, the concordance curve is defined by the pairs: $(i/n,\sum _{j=1}^{i}y_{{\hat{r}}_j}/(n{\bar{y}}))$, where ${\hat{r}}_i$ indicates the non-decreasing ranks of ${\hat{Y}}$.

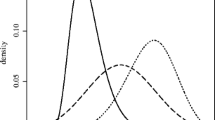
To visually describe the concordance curve, Fig. 1 reports, for a given test set $D_{test}$, the Lorenz curve, the dual Lorenz curve and the C concordance curve, together with the 45-degree line.

Fig. 1

The $L_Y$ and $L^{'}_{Y}$ Lorenz curves and the C concordance curve, where p (on the x-axis) and f(p) (on the y-axis) are the cumulative values of the x and y coordinates of the $L_Y$, $L^{'}_{Y}$ and C curves

From Fig. 1, note that the Lorenz curve and its dual are symmetric around the 45-degree line, and that the concordance curve lies between them (as shown in Raffinetti and Giudici 2012). When ${\hat{r}}_i =r_i,$ for all $i=1,\ldots ,n$, we have a perfect concordance: the concordance curve is equal to the Lorenz curve. When ${\hat{r}}_i = r_{n+1-i},$ for all $i=1,\ldots ,n$, we have perfect discordance: the concordance curve is equal to the dual Lorenz curve. In general, for any given point, the distance between the concordance curve and the Lorenz curve reveals how the rank of the predicted value differs from that of the best case, which is equal to the rank of the observed value. And, for any given point, the distance between the concordance curve and the dual Lorenz curve reveals how rank of the predicted value differs from that of the worst case, which is equal to the rank of the inversely ordered value.

The number of points on which the C curve in Fig. 1 is constructed is equal to the number of observations n. When the response variable is continuous, the observed and predicted values can take all possible real values. When the response variable is ordinal Y and ${\hat{Y}}$ can be replaced by the corresponding ranks R and ${\hat{R}}$, as illustrated in Giudici and Raffinetti (2022).

When the response variable is binary, taking one of two possible outcomes, corresponding to the presence ($Y=1$) or the absence ($Y=0$) of an attribute of interest, the predicted values take all possible real values in the interval [0, 1] which estimate the probability that $Y=1$. Indeed, in the binary case, the concordance C curve has a stepwise behavior, similar to the Receiver Operating Characteristic (ROC) curve (see e.g. Hand and Till 2011; DeLong et al. 1988).

In this paper we will show that, in the binary case, the ROC and the C curve are closely related. However, while the ROC curve can be used only for binary response variables, the C curve applies to all ordered response variables and, therefore, it can be applied to evaluate not only probability forecasts of categorical variables, but also point forecasts of continuous variables and ranks of ordinal variables. This generalisation led in Raffinetti (2023) to the construction of a Rank Graduation Accuracy measure (RGA), a summary measure of the C curve which can be applied to evaluate, in a similar fashion, the rank accuracy of probability forecasts, ordinal ranks and point predictions.

We will also show that, in the binary case, the RGA measure is equivalent to the AUROC measure, and can be employed to evaluate the accuracy of probability forecasts; whereas, in the real valued case, the RGA can be employed to evaluate the accuracy of rank and point forecasts, similarly to measures such as the RMSE. Differently from the latter, the RGA measure evaluates point predictions in terms of their ranks, rather than in terms of their values: losing scale precision but gaining robustness.

We remark that this work is related to the strand of literature that concerns the evaluation of point predictions, originated from the work in Gneiting (2011). Gneiting (2011) has introduced a very general framework to evaluate point forecasts by means of consistent scoring rules, specialized for the binary case in Gneiting and Raftery (2007); for the categorical case in Gneiting et al. (2008); for probability density forecasts in Gneiting and Ranjan (2011); for interval forecasts in Bracher and Gneiting (2021) and Bracher at al. (2021). While Gneiting (2011) and the related papers evaluate the accuracy of point predictions with respect to their actual values, as done by the RMSE in the continuous case, we evaluate the accuracy of the ranks of the point predictions, similarly to what is done by the AUROC in the binary case.

We also remark that this work is related to the papers that have studied the relationship between the Area Under the ROC Curve and the Gini coefficient (see e.g. Lee 1997; Hand and Till 2011; Gajowniczek et al. 2014). However, as highlighted by Schechtman and Schechtman (2019), the Gini coefficient is not an appropriate comparison benchmark, as it is based on only one variable, rather than on the comparison between two (conditional) variables, as the ROC Curve. A more appropriate comparison can be provided by the RGA, which is also based on one variable (the response), but ordered according to two different ranks (the observed and the predicted).

The remainder of the paper is organized as follows. Sections 2 and 3 present our proposal. Specifically, Sect. 2 shows the correspondence between the C concordance curve and the ROC curve in the binary case; Sect. 3 provides an overview of the RGA measure proposed by Raffinetti (2023) and introduces additional properties; Sect. 4 validates the RGA on simulated data; Sect. 5 illustrates a real application to the well known “Employee” data set; Sect. 6 concludes with a final discussion.

2 Correspondence between the C curve and the ROC curve

When the response variable is binary, the correspondence between the ROC curve and the C curve can be explained comparing their coordinates.

The ROC curve is a graphical plot of the predictive accuracy of the probability forecasts ${\hat{y}}_i \in [0,1]$ for a binary response $y_i \in \{0,1\}$, for $i=1,\ldots ,n$, conditional on a set of thresholds $t \in [0,1]$. The ROC curve is obtained joining $T \le n$ points which correspond to the chosen thresholds ordered by non-decreasing magnitude, plus the origin, for a total of $T+1$ points.

More formally, for $i=1,\ldots ,n$ and $t \in [0,1]$ define

$$\begin{aligned} I^{1}_{t}(y_i)=y_iI(p_i>t) \end{aligned}$$

(1)

and

$$\begin{aligned} I^{0}_{t}(y_i)=(1-y_i)I(p_i\le t), \end{aligned}$$

(2)

where $p_i$ is the predicted probability for i and $I(\cdot )$ is the indicator function.

The y coordinates of the ROC curve (the True Positive Rates), for $t=1,\ldots ,T$, are then equal to:

$$\begin{aligned} y^{ROC}_{t}=\frac{\sum _{i=1}^{n}I^{1}_{t}(y_i)}{\sum _{i=1}^{n}y_i}=\frac{\sum _{i=1}^{n}I^{1}_{t}(y_i)}{n_1}, \end{aligned}$$

(3)

whereas the x coordinates of the ROC Curve (the False Positive Rates) are equal to:

$$\begin{aligned} x^{ROC}_{t}=1-\frac{\sum _{i=1}^{n}I^{0}_{t}(y_i)}{\sum _{i=1}^{n}(1-y_i)}=\frac{n_0-\sum _{i=1}^{n}I^{0}_{t}(y_i)}{n_0}, \end{aligned}$$

(4)

with $n_1$ and $n_0$ indicating the number of Y values in the test set, respectively equal to 1 and to 0.

The C curve is a graphical plot of the predictive accuracy of the model forecasts ${\hat{y}}_i \in {\mathbb{R}}$ for an ordered response $y_i \in {\mathbb{R}}$, for $i=1,\ldots ,n$. The C curve is obtained joining n points which correspond to the observed values ordered by non-decreasing magnitude of the predictions, plus the origin, for a total of $n+1$ points.

More formally, for $i=1,\ldots ,n$, let $y_{{\hat{r}}_i}$ indicate the observed response values corresponding to the rank ${{\hat{r}}_i}$ of the predicted values, under the model being evaluated. The y coordinates are then equal to:

$$\begin{aligned} y^{C}_i=\frac{\sum _{j=1}^{i}y_{{\hat{r}}_j}}{\sum _{i=1}^{n}y_i}, \end{aligned}$$

(5)

whereas the x coordinate of the C curve can be expressed, for each observation i, as:

$$\begin{aligned} x^{C}_i=\frac{i}{n}. \end{aligned}$$

(6)

In the binary case, Eqs. (5) and (6) can be shown equal to:

$$\begin{aligned} y^{C}_i=\frac{\sum _{j=1}^{i}y_{{\hat{r}}_j}}{\sum _{i=1}^{n}y_i}=\frac{\sum _{j=1}^{i}y_{{\hat{r}}_j}}{n_1} \end{aligned}$$

(7)

and

$$\begin{aligned} x^{C}_i= \frac{i}{n}=\frac{\sum _{j=1}^{i}y_j+\sum _{j=1}^{i}(1-y_j)}{\sum _{i=1}^{n}y_i+\sum _{i=1}^{n}(1-y_i)}=\frac{\sum _{j=1}^{i}y_j+\sum _{j=1}^{i}(1-y_j)}{n_1+n_0}, \end{aligned}$$

(8)

respectively.

We now derive the relationship between the y-coordinates of the two curves. Assume that the threshold cut-off points are defined by $t=\frac{i}{n},$ for $i=1,\ldots ,n$, so that $T=n$. This implies that, for $j=1, \ldots , n$:

$$\begin{aligned} I^{1}_{t}(y_i)=I^{1}_{\big (\frac{i}{n}\big )}(y_j)=y_jI\bigg (p_j>\frac{i}{n}\bigg ) \end{aligned}$$

(9)

which leads to:

$$\begin{aligned} y^{ROC}_i=\frac{\sum _{j=1}^{n}I^{1}_{\big (\frac{i}{n}\big )}(y_j)}{\sum _{j=1}^{n}y_j}= \frac{\sum _{j=1}^{n}y_jI\bigg (p_j>\frac{i}{n}\bigg )}{\sum _{j=1}^{n}y_j}=\frac{\sum _{j=1}^{n}y_jI\bigg (p_j>\frac{i}{n}\bigg )}{n_1} \end{aligned}$$

(10)

and

$$\begin{aligned} y^{C}_i=\frac{\sum _{j=1}^{n}y_jI\bigg (rank(p_j)\le i\bigg )}{\sum _{j=1}^{n}y_j}=\frac{\sum _{j=1}^{n}y_jI\bigg (rank(p_j)\le i\bigg )}{n_1}, \end{aligned}$$

(11)

where $rank(p_j)$ refers to the ordered probabilities.

Comparing (10) with (11) note that the denominators are the same. The numerators are instead different: the C curve considers the ranks of the probability forecasts, rather than their values. This difference implies that the two curves are not straightforward transformation of one another although, as we show later, they can be used to derive two summary measures, the RGA and the AUROC, that coincide.

Before moving to the summary measures, it is useful to compare the C and ROC curves for some reference scenarios that occur in model comparison: the best case: a perfectly concordant model; the worst case: a perfectly discordant model; the random case, in which predictions are generated randomly and, finally, a generic “intermediate” case.

For the C curve:

i-c):

the best case occurs when the ordering of the Y response variable values corresponds to the ordering of the predicted values, with the C curve perfectly overlapping the Lorenz curve $L_Y$;

ii-c):

the worst case occurs when the ordering of the Y response variable values is in inverse correspondence with the ordering of the predicted values, with the C curve perfectly overlapping the dual Lorenz curve $L^{'}_{Y}$;

iii-c):

in the random case, the C curve overlaps the 45-degree line;

iv-c):

in the generic case, the C curve lies in the area between the Y response variable Lorenz curve, $L_Y$ and its dual, $L^{'}_{Y}$. The distance between C and the 45-degree line measures how a model improves over random predictions.

For the ROC curve:

(i-r):

the best case occurs when the ROC curve overlaps the y-axis, implying that both $Y=1$ and $Y=0$ are perfectly predicted by the model;

(ii-r):

the worst case occurs when the ROC curve overlaps the x-axis, implying that all the $Y=1$ are predicted as 0 and all the $Y=0$ are predicted as 1;

(iii-r):

in the random case, the ROC curve overlaps the 45-degree line;

(iv-r):

in the generic case, the ROC curve lies in the area between the x-axis and the y-axis. The distance between the ROC curve and the 45-degree line measures how a model improves over random predictions.

The stylised situations (i-c) and (i-r); (ii-c) and (ii-r); (iii-c) and (iii-r); (iv-c) and (iv-r) are illustrated from a graphical view point in Fig. 2.

Fig. 2

the C concordance curve and the ROC curve for the best, worst, random and generic possible cases. In this example $Y=\{1,0,1,1,0,0,0,1,0\}$. As in the best case, the 0 values preceed the 1 values, the cumulative percentage of the observations p (displayed on the x-axis) associated with the last 0 value, is approximately equal to the $55.6\%$ (i.e., 5/9). Whereas, in the worst case the cumulative percentage of the observations p associated with the last 1 value is approximately equal to the $44.4\%$ (i.e., 4/9)

3 The rank graduation accuracy measure

The AUROC measure (see e.g. Hand et al. 2001) is defined as the area under the ROC curve and, therefore, can assume any real value in the interval [0, 1], with AUROC$=$1 in the best case, AUROC$=$0.5 in the random case, and AUROC$=$0 in the worst case.

Note that the AUROC can be equivalently expressed as the ratio between the area under the model’s ROC and the area under the ROC of the best case, which is equal to 1.

Drawing on property iv-c) of the last section, a summary measure for the C curve of a model could be obtained considering the area between the dual Lorenz curve and the concordance curve, and dividing it by its maximum possible value: the area between the dual Lorenz curve and the Lorenz curve. This measure corresponds to the Rank Graduation Accuracy (RGA) proposed by Raffinetti (2023).

More formally, the Rank Graduation Accuracy (RGA) measure takes the following expression:

$$\begin{aligned} RGA=\frac{\sum _{i=1}^{n}\bigg \{\frac{1}{n{\bar{y}}} \big (\sum _{j=1}^{i}y_{r_{n+1-j}} -\sum _{j=1}^{i}y_{{\hat{r}}_j}\big )\bigg \}}{ \sum _{i=1}^{n}\bigg \{\frac{1}{n{\bar{y}}}\big ( \sum _{j=1}^{i}y_{r_{n+1-j}} -\sum _{j=1}^{i}y_{r_{j}}\big )\bigg \} }. \end{aligned}$$

(12)

It is worth noting that the RGA formula can be simplified as follows (see e.g., Raffinetti 2023):

$$\begin{aligned} RGA=\frac{\sum _{i=1}^{n}iy_{{\hat{r}}_i}-\sum _{i=1}^{n}iy_{r_{n+1-i}}}{\sum _{i=1}^{n}iy_{r_{i}}-\sum _{i=1}^{n}iy_{r_{n+1-i}}}. \end{aligned}$$

(13)

As mentioned in Raffinetti (2023), the RGA is defined in the close range [0, 1], fulfilling the normalisation property. In this paper, we further investigate the RGA features, introducing new additional properties. Before we do so, note that, when tied predictions occur, it may be unclear how to order the observed values in the expression of RGA. In this case, as highlighted by Raffinetti (2023), the suggestion provided by Ferrari and Raffinetti (2015), who proposed to replace the observed response values corresponding to the same predictions with their mean values, is considered.

Property 1

Normalisation. In general, $0 \le$ RGA $\le 1$, with RGA$=1$ in the best case of a perfectly concordant model; RGA$=0$ in the worst case of a perfectly discordant model; RGA$=0.5$ in the case of random predictions.

Note that the case of a response variable taking negative values was not present in the original definition of the Lorenz curves (see e.g. Lorenz 1905). However, Property 1 can be maintained. To see this, consider the following cases: (a) all the Y values are negative and, consequently, ${\bar{y}}<0$; (b) some Y values are positive and some are negative, with ${\bar{y}}>0$; (c) same as in (b) but ${\bar{y}}<0$. The three cases are displayed in Fig. 3a, b and c, respectively.

Fig. 3

Behaviour of the Lorenz curves for response variables taking negative values

From Fig. 3 note that, in case a), the Lorenz and dual Lorenz curves are reversed, but the Lorenz curves remain inside the unit square, satisfying Property 1. Differently, in cases b) and c), the Lorenz curve extends below $y=0$ and the dual Lorenz curve extends above $y=1$. In these cases, to fulfill Property 1, we can subtract from the Y variable its minimum negative value (see Ferrari and Raffinetti 2015). This translation leaves the measure invariant (see Property 2 below) and can thus be exploited to satisfy Property 1.

Property 2

Invariance. The RGA is invariant under all positive affine transformations of the form $Y\longmapsto aY+k$, where $a \in {\mathbb{R}}^+$ and $k \in {\mathbb{R}}$ are constants. It follows that RGA is invariant under transformations of the form $Y\longmapsto Y+k$, meaning that RGA$=$RGA$^k$, where RGA$^k$ denotes the RGA measure computed on the transformed variable $Y^k=Y+k$.

From Property 2, it follows in particular that adding a constant to a prediction does not affect the value of the RGA measure at all, a weakness that is shared by the AUROC measure (see e.g. Wilks 2011).

Property 3

Equivalence between RGA and AUROC. In the binary case, RGA$=$AUROC.

Property 4

Equivalence between the RGA and the Wilcoxon-Mann–Whitney statistic $W_1.$ In the binary case, RGA$=W_1$, the Wilcoxon-Mann–Whitney statistic (see Mason and Graham 2002).

The proofs of the aforementioned Properties are reported in Appendix.

Before validating our proposal on simulated and real data, a premise for the RGA results’ extension to the inferential perspective is reported in the following remark.

Remark 1

Following Raffinetti (2023) , a statistical test for the RGA measure can be derived by expressing it in terms of the covariance operator, as follows:

$$\begin{aligned} RGA=\frac{1}{2}\frac{cov(Y_{r({\hat{Y}})},F(Y))}{cov(Y,F(Y))}+\frac{1}{2}, \end{aligned}$$

(14)

where $Y_{r({\hat{Y}})}$ represents the Y variable re-ordered according to the ranks of the corresponding predictions ${\hat{Y}}$ and F is the cumulative continuous distribution function of Y.

It follows that the RGA is a linear function of the ratio:

$$\begin{aligned} \psi (Y,{\hat{Y}})=cov(Y_{r({\hat{Y}})},F(Y))/cov(Y,F(Y)). \end{aligned}$$

(15)

Given two alternative models ($Mod_1$ and $Mod_2$), the statistics in (15) can be used to test the following hypotheses:

$$\begin{aligned} H_0:\psi (Y,{\hat{Y}}_{Mod_1})=\psi (Y,{\hat{Y}}_{Mod_2})\quad \text{ vs } \quad H_1:\psi (Y,{\hat{Y}}_{Mod_1})\ne \psi (Y,{\hat{Y}}_{Mod_2}), \end{aligned}$$

(16)

where $\psi (Y,{\hat{Y}}_{Mod_1})=cov(Y_{r({\hat{Y}}_{Mod_1})},F(Y))/cov(Y,F(Y))$ and $\psi (Y,{\hat{Y}}_{Mod_2})=cov(Y_{r({\hat{Y}}_{Mod_2})},F(Y))/cov(Y,F(Y))$ are functions that derive from the application of (15), respectively to $RGA_{Mod_1}$ and $RGA_{Mod_2}$.

One can prove that the estimators ${\hat{\psi }}(Y,{\hat{Y}}_{Mod_1})$ and ${\hat{\psi }}(Y,{\hat{Y}}_{Mod_2})$ of $\psi (Y,{\hat{Y}}_{Mod_1})$ and $\psi (Y,{\hat{Y}}_{Mod_2})$ can be expressed in terms of U-statistics. Thus, the difference between the predictive accuracy associated with $Mod_1$ and $Mod_2$, corresponding to ${\hat{\delta }}={\hat{\psi }}(Y,{\hat{Y}}_{Mod_1})-{\hat{\psi }}(Y,{\hat{Y}}_{Mod_2})$, results as a function of independent U-statistics. According to Hoeffding (1948), a function of several dependent U-statistics has an asymptotic normal distribution. By applying the Jackknife method (see e.g., Efron and Stein 1981) for the ${\hat{\delta }}$ variance estimation, it derives that the test statistic for testing the null hypothesis $H_0:\psi (Y,{\hat{Y}}_{Mod_1})=\psi (Y,{\hat{Y}}_{Mod_2})$ is distributed according to a standard Normal distribution.

The proposed test can be extended, without loss of generality, to all types of ordinal variables. The continuity constraint of the joint distribution can be preserved replacing tied observations with their mean value. This adjustment gives rise to a continuous variable which, together with ${\hat{Y}}$, provides a continuous joint distribution.

4 Validation on simulated data

To illustrate the features of the proposed RGA, we set a simulation study generating a vector of seven random variables from a seven dimensional Gaussian distribution. One of the seven random variables is chosen to be the target variable, while the remaining six are assigned the role of predictors.

More precisely, we generate 1,000 observations from a seven-dimensional normal distribution with different degrees of correlation between the response variable Y and the six predictors $X_1,X_2,X_3,X_4,X_5,X_6$:

• Strong correlation between Y and $X_1$ ($\rho =0.8$);

• Quite strong correlation between Y and $X_2$ ($\rho =0.6$);

• Moderate correlation between Y and $X_3$ ($\rho =0.4$);

• Quite low correlation between Y and $X_4$ ($\rho =0.2$);

• No correlation between Y and the variables $X_5$ and $X_6$ ($\rho =0$).

In addition, we remark that variables $X_5$ and $X_6$ are not correlated with the other four predictors $X_1,X_2,X_3$ and $X_4$.

For completeness, we also consider the case in which the response variable Y is binarised, and compare the behavior of RGA for both a balanced and an unbalanced response. A balanced response is obtained binarising Y around its mean value (or median value) giving rise to a proportion of 1s approximately equal to 50%. An unbalanced response is obtained binarising Y around the first quartile, providing a proportion of 1s approximately equal to 75%.

While the continuous target variable Y is modeled through a linear regression, the binarised target variable Y is modeled through a logistic regression. For both classes of models, stepwise model selection are then applied to the simulated data. The available predictors are six and, for each possible model size, ranging from 1 to 6, we can compare all possible models by means of the Akaike Information Criterion (AIC), thereby identifying six candidate best models. We then split the dataset into a training dataset (including the 80% of all the observations) and a test dataset (including the remaining 20% of the observations), to calculate the RMSE and the RGA of the best linear regression models for each of the six dimensions, and subsequently, the BS and the RGA for the best logistic regression models. For both linear and logistic regressions, the models are ranked from the lowest RMSE and BS values, onwards; and from the highest RGA value, downwards.

The six explanatory variables appearing in the six best linear regression models are specified in Table 1 together with the values of the RMSE and RGA, computed on the test dataset. For completeness, the last column reports the AIC criterion, computed on the training dataset, for the same models. The behaviour of the predictive accuracy measures, referred to the different model sizes and measures, are graphically displayed in Fig. 4.

Table 1 Results from the linear regression models

Fig. 4

The AIC, RMSE and RGA behavior in the best 6 linear regression models

Figure 4 shows that the lowest AIC and RMSE and the highest RGA are obtained by Model 3, in which the significant predictors are $X_1,X_2$ and $X_3$. The result is coherent with the data structure as the three explanatory variables $X_1,X_2$ and $X_3$ are those which present the highest correlation with the target variable Y.

As the values of the RGA and RMSE associated with Model 3 are quite close to those referred to Model 2, with the aim of meeting the parsimony principle, we can try to further simplify the model assessing whether the predictive accuracies of Model 2 and Model 3 are significantly different. To this aim, the test illustrated in Remark 1, for the RGA, and the Diebold-Mariano test, for the RMSE, are employed. The application of the Diebold-Mariano test is appropriate as it is based on a function of the predicted errors (see Diebold and Mariano 1995). More precisely, given the predicted errors $e_{i_{Mod_{1}}}$ and $e_{i_{Mod_{2}}}$ associated with two alternative models $Mod_1$ and $Mod_2$, the null hypotheses to be tested is $E(d)=0$, where d is the test statistic $d=g(e_{i_{Mod_{1}}})-g(e_{i_{Mod_{2}}})$, which is asymptotically N(0, 1).

The results of the tests lead to select Model 3, as the p-values associated with the Diebold-Mariano and RGA tests are smaller than 0.01 and 0.02, respectively. This implies that Model 3 provides a predictive accuracy which is significantly better from that provided by Model 2.

In the case of logistic regression with both balanced and unbalanced data, the evaluation of the six best model configurations in terms of predictive accuracy involves the BS and RGA measures, together with the AIC criterion. The reason behind considering only the BS and not the AUROC, as a competitor of the RGA in the binary scenario, is motivated by the perfect equivalence between the RGA and the AUROC. Model comparison results are displayed in Tables 2 (for balanced data) and 3 (for unbalanced data).

Table 2 Results from the logistic regression models (balanced data)

From Table 2, it arises that variables $X_1,X_2$ and $X_3$ are the most relevant variables as they appear in all the six model configurations. Moreover, by looking at both Table 2 and Fig. 5, all the three measures led to select Model 3 as the best one. Indeed, Model 3 is associated with the lowest BS and AIC values and the the highest RGA value. The inclusion of the additional variable $X_5$ slightly worsens the model perfomance. This finding is coherent with what we obtained from the linear regression model.

Fig. 5

The AIC, BS and RGA behavior in the best 6 logistic regression models (balanced data)

Table 3 Results from the logistic regression models (unbalanced data)

For the unbalanced response case, Table 3 and Fig. 6 show that Model 2 is better than Model 3, having a lower value of BS and the same RGA as Model 3. On the other hand, the AIC (which is calculated on all data, and not only on the test set), continues to prefer Model 3. This is in line with the intuition that, with an unbalanced response, a simpler model is preferred, especially when working out of sample.

Fig. 6

The AIC, BS and RGA behavior in the best 6 logistic regression models (unbalanced data)

5 Application: employee data

In this section the publicly available “Employee” dataset, uploaded in the “stima” R package, is considered as an illustrative example of real data on which performing model selection with the RGA measure, in comparison with other measures, such as the RMSE (in the continuous case) and the AUROC and BS (in the binary case).

The data concerns a 1987 discrimination study carried out on 473 employees of a bank, and reports information on: gender, age, educational degree (in terms of years of education), employment category (custodial, clerical or manager), job time in months since hire, total work experience (total job time in months, since hire and from previous experiences), minority classification (that is, whether ethnic minority), starting salary (in dollars), current salary (in dollars). For a better description see e.g. Dusseldorp et al. (2010) and Ferrari and Raffinetti (2015).

Data is collected to understand, in particular, whether salary growth is affected by personal characteristics. To this aim, salary growth can be considered as a response variable, which can be measured either on a continuous scale, as the difference between the current salary and the starting salary, or on a binary scale, with level 1 achieved above a set increase from the starting to the current salary, and a level 0 otherwise. While the first scale is more informative and precise, the second is more interpretable and actionable.

In correspondence with the alternative specifications of the response variable, we consider two alternative classes of statistical models: linear and logistic regression. In the former case we select as a response variable the salary growth. In the latter case we fix as a reference threshold the “doubling" of the starting salary (which approximately corresponds to the ratio between current and starting salaries) and, consequently, set $Y=1$ when the ratio between the current and the starting salary is greater or equal than 2, and $Y=0$ otherwise. We then follow the same procedure considered in Sect. 4: for both classes of models, stepwise model selection is applied to the data. The candidate predictors are eight: the previously described variables (excluding the current and starting salary), with the employment category transformed in two binary variables: “custodial" and “manager" (with “clerical" kept as baseline).

All possible models, characterised by different size (from 1 to 8 predictors), are evaluated in terms of the AIC criterion in order to detect the eight candidate best models. We then apply cross-validation by splitting the whole dataset into training and test datasets with the same percentage of observations we specified for the case of simulated data. Finally, the RMSE and the RGA of the best linear regression models together with the BS and the RGA of the best logistic regression models (for each of the eight dimensions), are computed. The models are then ranked, as described in Sect. 4, from the lowest RMSE and BS values, onwards; and from the highest RGA value, downwards.

Starting from linear regression, Table 4 reports the variables included in the best eight models and the related RMSE, RGA, and AIC measures. As mentioned in Sect. 4, RMSE and RGA are computed on the test dataset, while AIC is calculated on the training dataset.

Table 4 Results from the linear regression models

From Table 4 note that the most important variables, present in most selected models, are: employment category (manager), job time and educational degree. To better visualize the behavior of the predictive accuracy metrics, Fig. 7 displays their values as model size increases.

Fig. 7

The AIC, RMSE and RGA behavior in the best 8 linear regression models

From Fig. 7 note that the lowest AIC and RMSE and the highest RGA are obtained in correspondence with Model 7, for which the variables mostly impacting on the salary growth are: employment category (manager, custodial), education degree, job time and tot. job time, gender (male) and minority (no-minority).

Note that, when including in the model also the age explanatory variable, the predictive accuracy of the model worsens, as both the RMSE and AIC values increase, while the RGA value decreases.

We can confirm the model selection results testing the null hypothesis that Model 7 and Model 8 have the same predictive accuracy, applying the RGA-based test and the Diebold-Mariano test for the RMSE. The results show that the p-values associated with the Diebold-Mariano and RGA tests are equal to 0.3917 and 0.3478, respectively, implying that Model 7 provides a predictive accuracy which is not significantly different from that provided by Model 8. According to the parsimony principle, Model 7 is to be preferred.

The results from logistic regression model selection are provided in Table 5, which contains the BS and RGA measures computed on the test set along with the corresponding AIC criterion computed on the training dataset.

Table 5 Results from the logistic regression models

From Table 5, note that the most important variables, present in most selected models, are: age, job time and the employment category (custodial, manager). Figure 8 displays the behaviour of the predictive accuracy metrics, in correspondence to different model dimensions.

Fig. 8

The AIC, BS and RGA behavior in the best 8 logistic regression models

Figure 8 shows, as for the linear regression model, that AIC, BS and RGA select the same model: Model 5, which includes the variables age, job time, employment category (manager, custodial) and gender (male).

Note that, as the RGA is an agnostic approach for evaluating the predictive accuracy of models characterised by different type of outcome variables, we can also directly compare the logistic with the linear models. It turns out that ethnicity minority, total jobtime and educational degree do not affect the probability of doubling the salary, but only the salary growth. Similarly, age does not impact the salary growth. Based on the RGA, the best performance is achieved by the model built on the salary growth rather than on doubling the salary, as it provides a gain in terms of predictive accuracy of almost 14%. In other words, for the available data, the given predictors are more accurate for a continuous response than for a binary response.

6 Conclusive comments

This paper exemplifies the importance of statistics for Artificial Intelligence, in line with what discussed in Friedrich et al. (2022). Specifically, we have further analysed the RGA measure, proposed as a new tool to evaluate the predictive accuracy of a machine learning model. In this paper we have shown that the RGA can extend the application of the well known AUROC measure from the case of a binary response variable to a more general setting, that includes also continuous and ordered response variables. To achieve this aim we have considered the concordance curve, and demonstrated its correspondence with the ROC curve, along with the statistical properties that allow the extension of the ROC and the AUROC beyond the binary case. Doing so, we extend the application of the AUROC measure, and overcome its limitations, as underlined by Hand and Anagnostopoulos (2023) and Vivo et al. (2018).

From a methodological viewpoint, the RGA measure provides a rather general accuracy statistic, applicable in the same manner to all ordered response variables. It is preferable to other measures when the purpose is to predict the correct ordering of a point response, regardless of whether such response is binary, ordinal or continuous. In all cases, the predictions enter into the concordance curve calculation (from which the RGA is derived) only via their ranks. This means that two forecasts with the same prediction ranks get assigned the same RGA, regardless of the actual predictions. If the aim of the research is to predict the rank of the predicted values, the RGA is perfectly appropriate and, indeed, more appropriate than measures such as the RMSE. If, instead, the aim is to predict the actual values of a point response, the RMSE and similar measures may be more suitable.

It is however worth noting that an important benefit related to the employment of the RGA is its capability of being robust to the presence of outlying observations which may affect the predictors and, consequently, the derived predictions. This advantage is especially evident when the response to be predicted is continuous (as the salary growth in the “Employee” dataset example). The RGA is indeed more robust than alternative standard predictive accuracy measures, such as the RMSE and the Huber loss, which may strongly depend on anomalous observations.

In the paper, the RGA has been applied and validated to both simulated and real data. For the simulated data case, we have considered both a continuous and a binary target variable, balanced and unbalanced. In line with the analysis presented by Chaabane et al. (2020), the unbalanced case leads to simpler models. The real data analysis has allowed to directly compare, in terms of predictive accuracy, linear regression with logistic regression.

Given the generality of the RGA, the paper shows that the evaluation of the predictive accuracy of a model can be extended to the evaluation of the accuracy of a model under alternative representations of the response variable (binary, ordinal, continuous). In this way, researchers may investigate the measurement scale for the response variable which appears the best one to obtain good predictions.

Future research may involve the application of the RGA measure to the assessment of further trustworthy AI principles, besides Accuracy, such as Sustainability, Fairness and Explainability, extending the recent works of Vojíř and Kliegr (2020), Giudici and Raffinetti (2021) and Giudici et al. (2023).

Appendices

Appendix

In this appendices the proofs of Properties 1, 2, 3 and 4 are reported.

Appendix A proof of property 1

Let us suppose that Y takes non-negative values, $Y \in {\mathbb {R}}^{+}$. When this is not so, a transformation can be applied (as in Ferrari and Raffinetti 2015), leading to a new variable $Y^+=Y-y^-$, taking values in ${\mathbb {R}}^{+}$, where $y^-=min(0,y_{min})$ is the minimum of Y.

• i) The first condition to be proved is RGA$\le 1$, meaning that

  $$\begin{aligned} RGA=\frac{\sum _{i=1}^{n}iy_{{\hat{r}}_i}-\sum _{i=1}^{n}iy_{r_{n+1-i}}}{\sum _{i=1}^{n}iy_{r_{i}}-\sum _{i=1}^{n}iy_{r_{n+1-i}}}\le 1\Longleftrightarrow \frac{\sum _{i=1}^{n}iy_{{\hat{r}}_i}-\sum _{i=1}^{n}iy_{r_{i}}}{\sum _{i=1}^{n}iy_{r_{i}}-\sum _{i=1}^{n}iy_{r_{n+1-i}}} \le 0. \end{aligned}$$

  (A.1)

  As $-\sum _{i=1}^{n}iy_{r_{n+1-i}}=\sum _{i=1}^{n}iy_{{\hat{r}}_i}-n(n+1){\bar{y}}$ (see e.g. Marshall et al. 2011), it follows that inequality in (A.1) becomes

  $$\begin{aligned} \frac{\sum _{i=1}^{n}iy_{{\hat{r}}_i}-\sum _{i=1}^{n}iy_{r_{i}}}{2\sum _{i=1}^{n}iy_{r_{i}}-n(n+1){\bar{y}}}\le 0. \end{aligned}$$

  (A.2)

  As the denominator $2\sum _{i=1}^{n}iy_{r_{i}}-n(n+1){\bar{y}}>0$ (see e.g. Ferrari and Raffinetti 2015), to demonstrate that equation (A.2) is smaller or equal than zero, we have to prove that $\sum _{i=1}^{n}iy_{{\hat{r}}_i}-\sum _{i=1}^{n}iy_{r_{i}} \le 0$ and, consequently:

  $$\begin{aligned} \sum _{i=1}^{n}iy_{{\hat{r}}_i}\le \sum _{i=1}^{n}iy_{r_{i}}. \end{aligned}$$

  (A.3)

  As stated by Marshall et al. (2011), it results that $\sum _{j=1}^{i}y_{{\hat{r}}_j} \ge \sum _{j=1}^{i}y_{r_{j}}$, meaning that $\sum _{i=1}^{n}\sum _{j=1}^{i}y_{{\hat{r}}_j}\ge \sum _{i=1}^{n}\sum _{j=1}^{i}y_{r_j}$. Because of the relationships $\sum _{i=1}^{n}\sum _{j=1}^{i}y_{{\hat{r}}_j}=n(n+1){\bar{y}}-\sum _{i=1}^{n}iy_{{\hat{r}}_i}$ and $\sum _{i=1}^{n}\sum _{j=1}^{i}y_{r_j}=n(n+1){\bar{y}}-\sum _{i=1}^{n}iy_{r_i}$, it follows that $n(n+1){\bar{y}}-\sum _{i=1}^{n}iy_{{\hat{r}}_i}\ge n(n+1){\bar{y}}-\sum _{i=1}^{n}iy_{r_i}$, implying that $\sum _{i=1}^{n}iy_{{\hat{r}}_i}\le \sum _{i=1}^{n}iy_{r_i}$ which is equivalent to the inequality in (A.3). The second condition to be proved is RGA$\ge 0$, meaning that

  $$\begin{aligned} RGA=\frac{\sum _{i=1}^{n}iy_{{\hat{r}}_i}-\sum _{i=1}^{n}iy_{r_{n+1-i}}}{\sum _{i=1}^{n}iy_{r_{i}}-\sum _{i=1}^{n}iy_{r_{n+1-i}}}\ge 0. \end{aligned}$$

  (A.4)

  As previously remarked, the denominator in (A.4) can be equivalently expressed as $2\sum _{i=1}^{n}iy_{r_{i}}-n(n+1){\bar{y}}$, always greater than zero. Thus, to show that equation (A.4) is greater or equal than zero, we have to prove that $\sum _{i=1}^{n}iy_{{\hat{r}}_i}-\sum _{i=1}^{n}iy_{r_{n+1-i}} \ge 0$ and consequently

  $$\begin{aligned} \sum _{i=1}^{n}iy_{{\hat{r}}_i}\ge \sum _{i=1}^{n}iy_{r_{n+1-i}}\end{aligned}.$$

  (A.5)

  From Marshall et al. (2011), it derives that

  $$\begin{aligned} \sum _{j=1}^{i}y_{{\hat{r}}_j}\le \sum _{j=1}^{i}y_{r_{n+1-j}}\end{aligned}.$$

  (A.6)

  As the inequality in (A.6) is true for any i, we also have that $\sum _{i=1}^{n}\sum _{j=1}^{i}y_{{\hat{r}}_j}\le \sum _{i=1}^{n}\sum _{j=1}^{i}y_{r_{n+1-j}}$, where $\sum _{i=1}^{n}\sum _{j=1}^{i}y_{{\hat{r}}_j}=n(n+1){\bar{y}}-\sum _{i=1}^{n}{i}y_{{\hat{r}}_i}$ and $\sum _{i=1}^{n}\sum _{j=1}^{i}y_{r_{n+1-j}}=n(n+1){\bar{y}}-\sum _{i=1}^{n}iy_{r_{n+1-i}}$. Thus, $\sum _{i=1}^{n}iy_{{\hat{r}}_i}\ge \sum _{i=1}^{n}iy_{r_{n+1-i}}$.

• ii) The scenario RGA$=$1 is achieved if, from Eq. (13), the relation $\sum _{i=1}^{n}iy_{{\hat{r}}_i}=\sum _{i=1}^{n}iy_{r_{i}}$ is fulfilled, meaning that ${\hat{r}}_i=r_{i}$, for all $i=1,\ldots ,n$.

• iii) The scenario RGA$=$0 is achieved if, from Eq. (13), it results that $\sum _{i=1}^{n}iy_{{\hat{r}}_i}=\sum _{i=1}^{n}iy_{r_{n+1-i}}$, meaning that ${\hat{r}}_i=r_{n+1-i}$, for all $i=1,\ldots ,n$.

• iv) Note that, as $\sum _{i=1}^{n}iy_{r_{i}}=n(n+1){\bar{y}}-\sum _{i=1}^{n}iy_{r_{n+1-i}}$, we replace, in Eq. (13), the term $-\sum _{i=1}^{n}iy_{r_{n+1-i}}$ with $\sum _{i=1}^{n}iy_{r_i}-n(n+1){\bar{y}}$, leading to

  $$\begin{aligned} RGA=\frac{\sum _{i=1}^{n}iy_{{\hat{r}}_i}+\sum _{i=1}^{n}iy_{r_i}-n(n+1){\bar{y}}}{\sum _{i=1}^{n}iy_{r_i}+\sum _{i=1}^{n}iy_{r_i}-n(n+1){\bar{y}}} =\frac{\sum _{i=1}^{n}iy_{{\hat{r}}_i}+\sum _{i=1}^{n}iy_{r_i}-n(n+1){\bar{y}}}{2\sum _{i=1}^{n}iy_{r_i}-n(n+1){\bar{y}}}\nonumber . \end{aligned}$$

  (A.7)

  Thus, the random case is reached if the model generates predicted values all equal to each other, so that the observed target variable values can be replaced by the mean value ${\bar{y}}$. In this case, it results that $y_{{\hat{r}}_i}={\bar{y}}$ (for all $i=1,\ldots ,n$) and equation (A.7) becomes

  $$\begin{aligned} RGA=\frac{{\bar{y}}\sum _{i=1}^{n}i+\sum _{i=1}^{n}iy_{r_i}-n(n+1){\bar{y}}}{2\sum _{i=1}^{n}iy_{r_i}-n(n+1){\bar{y}}}. \end{aligned}$$

  (A.8)

  Given that $\sum _{i=1}^{n}i=\frac{n(n+1)}{2}$, equation in (A.8) can then be re-written as

  $$\begin{aligned} RGA=\frac{{\bar{y}}\frac{n(n+1)}{2}+\sum _{i=1}^{n}iy_{r_i}-n(n+1){\bar{y}}}{2\sum _{i=1}^{n}iy_{r_i}-n(n+1){\bar{y}}}=\frac{1}{2}\frac{[\sum _{i=1}^{n}iy_{r_i}-\frac{n(n+1)}{2}{\bar{y}}]}{[\sum _{i=1}^{n}iy_{r_i}-\frac{n(n+1)}{2}{\bar{y}}]} =0.5. \end{aligned}$$

Appendix B Proof of property 2

We have to prove that RGA=RGA$^k$, where $Y^k=Y+k$, with $k \in {\mathbb {R}}$.

As $\sum _{i=1}^{n}i=\frac{n(n+1)}{2}$, RGA$^k$ can be computed as

$$\begin{aligned} RGA^k&=\frac{\sum _{i=1}^{n}i(y_{{\hat{r}}_i}+k)-\sum _{i=1}^{n}i(y_{r_{n+1-i}}+k) }{\sum _{i=1}^{n}i(y_{r_{i}}+k)-\sum _{i=1}^{n}i(y_{r_{n+1-i}}+k)}\\&=\frac{\sum _{i=1}^{n}iy_{{\hat{r}}_i}+k\frac{n(n+1)}{2}-\sum _{i=1}^{n}iy_{r_{n+1-i}}-k\frac{n(n+1)}{2}}{\sum _{i=1}^{n}iy_{r_{i}}+k\frac{n(n+1)}{2}-\sum _{i=1}^{n}y_{r_{n+1-i}}-k\frac{n(n+1)}{2}}\\&=\frac{\sum _{i=1}^{n}iy_{{\hat{r}}_i}-\sum _{i=1}^{n}iy_{r_{n+1-i}}}{\sum _{i=1}^{n}iy_{r_{i}}-\sum _{i=1}^{n}iy_{r_{n+1-i}}}, \end{aligned}$$

which corresponds to the RGA formula in equation (13).

Appendix C Proof of property 3

The equivalence RGA$=$AUROC implies that the area under the ROC curve equals the area lying between the dual Lorenz curve and the C curve.

If on the one hand, the area under the ROC curve can be intended as the distance between the ROC curve corresponding to the worst case (coinciding with the x-axis) and the ROC curve associated with the generic case, on the other hand the area between the dual Lorenz curve and the C curve depends on the distance between the C curve associated with the worst case and the C curve associated with the generic case.

For the sake of clarity, in Fig. 9, a graphical illustration of all the areas involved for the calculation of RGA is reported.

Fig. 9

Areas involved for the RGA computation

From Fig. 9 note that the distance between the dual Lorenz curve ($L^{'}_{Y}$) and the C curve, denoted with $\Delta _{DC}$, is equal to the sum of AREA 1 with AREA 2. Let S indicate the area under $L^{'}_{Y}$, corresponding to the area of a trapezoid. From Fig. 9 we have that AREA 1+AREA 2= S-(AREA 3+AREA 4), where AREA 3+AREA 4 represents the area under the C curve which can also be computed by applying the trapezoid rule.

Before proceeding, let us recall the general trapezoid rule. Let $\{x_k\}$ be a partition of [a, b], such that $a=x_0<x_1<\ldots<x_{n-1}<x_n=b$, and $\Delta x$ be the length of the k-th subinterval (where $\Delta x=x_k-x_{k-1}$). The area under a curve referred to a partition [a, b] is determined as $\Delta x\bigg [\frac{f(x_0)+f(x_n)}{2}+\sum _{k=1}^{n-1}f(x_k)\bigg ]$, where f is a generic function and $f(x_k)$ is the y-axis value of the points included in the consider partition, with $k=1,\ldots ,n$.

By applying the trapezoid rule to Fig. 9, it follows that

$$\begin{aligned} \Delta _{DC}=\frac{1}{n}\Bigg [n_0+\frac{n_1}{2}\Bigg ]-\frac{1}{n}\Bigg [\frac{1}{2}+\sum _{i=1}^{n-1}\sum _{j=1}^{i}\frac{y_{{\hat{r}}_j}}{n_1}\Bigg ]=\frac{1}{n}\Bigg [n_0+\frac{n_1}{2}-\frac{1}{2}-\sum _{i=1}^{n-1}\sum _{j=1}^{i}\frac{y_{{\hat{r}}_j}}{n_1}\Bigg ]. \end{aligned}$$

To normalise the area between the dual Lorenz curve and the C curve, $\Delta _{DC}$ has to be divided by the distance between the dual Lorenz curve ($L^{'}_{Y}$) and the Lorenz curve ($L_{Y}$), which we denote with $\Delta _{DL}$. The latter is equivalent to the difference between the area of the trapezoid S and AREA 4:

$$\begin{aligned} \Delta _{DL}=\frac{1}{n}\Bigg [n_0+\frac{n_1}{2}\Bigg ]-\frac{1}{n}\frac{n_1}{2}=\frac{n_0}{n}=p_0, \end{aligned}$$

where $p_0=n_0/n$ is the prevalence ratio of negatives (0’s) in the dataset. As by definition RGA compares the distance between the generic case and the worst case (at the numerator) with the distance between the best case and the worst case (at the denominator), it follows that:

$$\begin{aligned} RGA=\frac{\Delta _{DC}}{\Delta _{DL}}=\frac{\frac{1}{n}\Bigg [n_0+\frac{n_1}{2}\Bigg ]-{\frac{1}{n}\Bigg [\frac{1}{2}+\sum _{i=1}^{n-1}\sum _{j=1}^{i}\frac{y_{{\hat{r}}_j}}{n_1}\Bigg ]}}{p_0}. \end{aligned}$$

(A.9)

Note that the denominator of equation (A.9) specifies the maximum possible distance between two C curves: that between the worst and the best case. Thus, the area lying between the dual Lorenz curve and the Lorenz curve measures the maximum space within which the C curve moves and, for this reason, it takes the role of a normalising factor.

On the other hand, the AUROC can be derived through the trapezoid rule as follows:

$$\begin{aligned} AUROC=\frac{1}{n}\Bigg [\frac{1}{2}+\sum _{i=1}^{n-1}\sum _{j=1}^{n}\frac{y_jI\big (p_j>\frac{i}{n}\big )}{n_1}\Bigg ]. \end{aligned}$$

(A.10)

To interpret the AUROC in analogy with the RGA measure, we can write it in terms of a ratio of the distance between the ROC curves associated with the worst case (corresponding to the line $y=0$) and the model under evaluation with the distance between the ROC curves associated with the best case and the worst case (corresponding to the distance between the lines $y=1$ and $y=0$), as follows:

$$\begin{aligned} AUROC=\frac{0-\frac{1}{n}\Bigg [\frac{1}{2}+\sum _{i=1}^{n-1}\sum _{j=1}^{n}\frac{y_jI\big (p_j>\frac{i}{n}\big )}{n_1}\Bigg ]}{0-1}=\frac{\frac{1}{n}\Bigg [\frac{1}{2}+\sum _{i=1}^{n-1}\sum _{j=1}^{n}\frac{y_jI\big (p_j>\frac{i}{n}\big )}{n_1}\Bigg ]}{\frac{n}{n}}. \end{aligned}$$

(A.11)

From equation (A.11), note that n/n represents the area lying between the ROC curve associated with the best case and that of the the worst case, and identifies the maximum space within which the ROC curve of a model moves. Thus, as for the RGA in formula (A.9), it takes the role of a normalising factor. As the ROC curve is located above the 45-degree line, contrary to the C curve which is located below, to reach the equivalence between RGA and AUROC, equation (A.11) has to be multiplied by -1, that is:

$$\begin{aligned} AUROC=-\frac{\frac{1}{n}\Bigg [\frac{1}{2}+\sum _{i=1}^{n-1}\sum _{j=1}^{n}\frac{y_jI\big (p_j>\frac{i}{n}\big )}{n_1}\Bigg ]}{\frac{n}{n}}. \end{aligned}$$

(A.12)

Comparing (A.9) with (A.12) it follows that AUROC$=$RGA.

Appendix D Proof of Property 4

We have to prove that, when dealing with a binary target variable, RGA$=W_1$, the Wilcoxon-Mann–Whitney statistic.

The Wilcoxon-Mann–Whitney statistic $W_1$ is defined as

$$\begin{aligned} W_1=\frac{R_1-\frac{n_1(n_1+1)}{2}}{n_0n_1}, \end{aligned}$$

(A.13)

where $n_1$ is the frequency of the $y=1$ (positive cases); $n_0$ is the frequency of the $y=0$ (negative cases); $n=n_0+n_1$; $R_1$ is the sum of the ranks of the predicted values for all positive cases ($y=1$).

We start by proving the equivalence between the $W_1$ and RGA denominators, that is

$$\begin{aligned} \sum _{i=1}^{n}iy_{r_{i}}-\sum _{i=1}^{n}iy_{r_{n+1-i}}=n_0n_1. \end{aligned}$$

(A.14)

Let us consider the second term of the RGA denominator, $\sum _{i=1}^{n}iy_{r_{n+1-i}}$, which can be simplified as $\sum _{i=1}^{n_1}i=\frac{n_1(n_1+1)}{2}$, being the values re-ordered in a non-increasing sense and implying that the first $n_1$ values of Y are equal to 1. By resorting to an arithmetic progression, the first term of the RGA denominator, $\sum _{i=1}^{n}iy_{r_{i}}$, can be simplified as $\bigg [\frac{n_0+1+n}{2}\bigg ][n-n_0]$. This implies that

$$\begin{aligned} \sum _{i=1}^{n}iy_{r_{i}}-\sum _{i=1}^{n}iy_{r_{n+1-i}}&=\frac{n_0+1+n}{2}[n-n_0]-\frac{n_1(n_1+1)}{2}\\ &=\frac{n_0+1+n}{2}n_1-\frac{n_1(n_1+1)}{2}\\&=\frac{n_1}{2}[n_0+1+n-n_1-1]=\frac{n_1}{2}[2n_0]=n_0n_1. \end{aligned}$$

We have now to show the equivalence between the two numerators, i.e. $\sum _{i=1}^{n}iy_{{\hat{r}}_i}-\sum _{i=1}^{n}iy_{r_{n+1-i}}=R_1- \frac{n_1(n_1+1)}{2}$, implying that $R_1=\sum _{i=1}^{n}iy_{{\hat{r}}_i}$, as we already proved that $\sum _{i=1}^{n}iy_{r_{n+1-i}}=\frac{n_1(n_1+1)}{2}$.

To achieve this, consider the scenario of tied predictions. In this case, both the RGA and the $W_1$ statistic involve a specific adjustment. For the RGA computation, the average of the observed values, associated with the same predicted scores, is computed; for the $W_1$ statistic computation, the average rank of the tied predicted scores is calculated.

Let us suppose that the sequence of the n predicted scores presents m tied values, so that $m<n$. Based on the adjustment for tied values, it results that the RGA computation involves the term

$$\begin{aligned} \sum _{l=1}^{m}\frac{y_l}{m}r({\hat{y}}_l), \end{aligned}$$

(A.15)

where $r({\hat{y}}_l)$ is the rank assigned (according to the predicted scores) to the l-th observation, in the case of non-tied values, and $y_l$ is the observed value taken by the binary response variable $(y_l\in \{0;1\})$. Formula (A.15) can be re-expressed as

$$\begin{aligned} \sum _{l=1}^{m}y_l\frac{r({\hat{y}}_l)}{m}=\sum _{l=1}^{m}y_l{\bar{r}}({\hat{y}}_l), \end{aligned}$$

(A.16)

where ${\bar{r}}({\hat{y}}_l)$ is the average rank of the l-th y value.

Although the term $R_1$ in equation (A.13) represents the sum of the ranks of the positive cases (with respect to the predicted scores), we can re-express it including also the negative cases. Indeed, $R_1$ preserves its value if we extend the summation to the ranks of the negative cases. Specifically, without tied values, this is equivalent to multiply the y values equal to 1 and 0 by the ranks of the corresponding predicted scores, respectively.

Clearly, multiplying the values of 0’s by the ranks of the corresponding predicted scores gives that $R_1$ reduces to the summation involving only the ranks associated with the positive cases, leading to $R_1=\sum _{l=1}^{n}y_ir({\hat{y}}_i)$.

As $i=r({\hat{y}}_i)$, for any $i=1,\ldots ,n$, it follows that $\sum _{i=1}^{n}iy_{{\hat{r}}_i}=\sum _{i=1}^{n}y_ir({\hat{y}}_i)$.

In the case of tied values, it results that $R_1$ involves the term

$$\begin{aligned} \sum _{l=1}^{m}y_l{\bar{r}}({\hat{y}}_l)=\sum _{l=1}^{m}y_l\frac{r({\hat{y}}_l)}{m}=\sum _{l=1}^{m}\frac{y_l}{m}r({\hat{y}}_l), \end{aligned}$$

(A.17)

which corresponds to the term reported in equation (A.15), providing the equivalence between the RGA and the $W_1$ statistic.