An augmented Lagrangian method for optimization problems with structured geometric constraints

Abstract

This paper is devoted to the theoretical and numerical investigation of an augmented Lagrangian method for the solution of optimization problems with geometric constraints. Specifically, we study situations where parts of the constraints are nonconvex and possibly complicated, but allow for a fast computation of projections onto this nonconvex set. Typical problem classes which satisfy this requirement are optimization problems with disjunctive constraints (like complementarity or cardinality constraints) as well as optimization problems over sets of matrices which have to satisfy additional rank constraints. The key idea behind our method is to keep these complicated constraints explicitly in the constraints and to penalize only the remaining constraints by an augmented Lagrangian function. The resulting subproblems are then solved with the aid of a problem-tailored nonmonotone projected gradient method. The corresponding convergence theory allows for an inexact solution of these subproblems. Nevertheless, the overall algorithm computes so-called Mordukhovich-stationary points of the original problem under a mild asymptotic regularity condition, which is generally weaker than most of the respective available problem-tailored constraint qualifications. Extensive numerical experiments addressing complementarity- and cardinality-constrained optimization problems as well as a semidefinite reformulation of MAXCUT problems visualize the power of our approach.

1 Introduction

We consider the program

where and are Euclidean spaces, i.e., real and finite-dimensional Hilbert spaces, $f:{\mathbb {W}} \rightarrow {\mathbb {R}}$ and $G:{\mathbb {W}} \rightarrow {\mathbb {Y}}$ are continuously differentiable, $C \subset {\mathbb {Y}}$ is nonempty, closed, and convex, whereas the set $D \subset {\mathbb {W}}$ is only assumed to be nonempty and closed. This setting is very general and covers, amongst others, standard nonlinear programs, second-order cone and, more generally, conic optimization problems [14, 24], as well as several so-called disjunctive programming problems like mathematical programs with complementarity, vanishing, switching, or cardinality constraints, see [15, 16, 29, 56] for an overview and suitable references. Since ${\mathbb {W}}$ and ${\mathbb {Y}}$ are Euclidean spaces, our model also covers matrix optimization problems like semidefinite programs or low-rank approximation problems [53].

The aim of this paper is to apply a (structured) augmented Lagrangian technique to (P) in order to find suitable stationary points. The augmented Lagrangian or multiplier penalty method is a classical approach for the solution of nonlinear programs, see [17] as a standard reference. The more recent book [18] presents a slightly modified version of this classical augmented Lagrangian method, which uses a safeguarded update of the Lagrange multipliers and has stronger global convergence properties. In the meantime, this safeguarded augmented Lagrangian method has also been applied to a number of optimization problems with disjunctive constraints, see e.g. [5, 33, 42, 45, 61].

Since, to the best of our knowledge, augmented Lagrangian methods have not yet been applied to the general problem (P) with general nonconvex D and arbitrary convex sets C in the setting of Euclidean spaces, and in order to get a better understanding of our contributions, let us add some comments regarding the existing results for the probably most prominent non-standard optimization problem, namely the class of mathematical programs with complementarity constraints (MPCCs). Due to the particular structure of the feasible set, the usual Karush–Kuhn–Tucker (KKT for short) conditions are typically not satisfied at a local minimum. Hence, other (weaker) stationarity concepts have been proposed, like C- (abbreviating Clarke) and M- (for Mordukhovich) stationarity, with M-stationarity being the stronger concept. Most algorithms (regularization, penalty, augmented Lagrangian methods etc.) for the solution of MPCCs solve a sequence of standard nonlinear programs, and their limit points are typically C-stationary points only. Some approaches can identify M-stationary points if the underlying nonlinear programs are solved exactly, but they loose this desirable property if these programs are solved only inexactly, see the discussion in [47] for more details.

The authors are currently aware of only three approaches where convergence to M-stationary points for a general (nonlinear) MPCC is shown using inexact solutions of the corresponding subproblems, namely [9, 33, 61]. All three papers deal with suitable modifications of the (safeguarded) augmented Lagrangian method. The basic idea of reference [9] is to solve the subproblems such that both a first- and a second-order necessary optimality condition hold inexactly at each iteration, i.e., satisfaction of the second-order condition is the central point here which, obviously, causes some overhead for the subproblem solver and usually excludes the application of this approach to large-scale problems. The paper [61] proves convergence to M-stationary points by solving some complicated subproblems, but for the latter no method is specified. Finally, the recent approach described in [33] provides an augmented Lagrangian technique for the solution of MPCCs where the complementarity constraints are kept as constraints, whereas the standard constraints are penalized. The authors present a technique which computes a suitable stationary point of these subproblems in such a way that the entire method generates M-stationary accumulation points for the original MPCC. Let us also mention that [36] suggests to solve (a discontinuous reformulation of) the M-stationarity system associated with an MPCC by means of a semismooth Newton-type method. Naturally, this approach should be robust with respect to (w.r.t.) an inexact solution of the appearing Newton-type equations although this issue is not discussed in [36].

The present paper universalizes the idea from [33] to the much more general problem (P). In fact, a closer look at the corresponding proofs shows that the technique from [33] can be generalized using some relatively small modifications. This allows us to concentrate on some additional new contributions. In particular, we prove convergence to an M-type stationary point of the general problem (P) under a very weak sequential constraint qualification introduced recently in [54] for the general setting from (P). We further show that this sequential constraint qualification holds under the conditions for which convergence to M-stationary points of an MPCC is shown in [33]. Note that this is also the first algorithmic application of the general sequential stationarity and regularity concepts from [54].

The global convergence result for our method holds for the abstract problem (P) with geometric constraints without any further assumptions regarding the sets C and, in particular, D. Conceptually, we are therefore able to deal with a very large class of optimization problems. On the other hand, we use a projected gradient-type method for the solution of the resulting subproblems. Since this requires projections onto the (usually nonconvex) set D, our method can be implemented efficiently only if D is simple in the sense that projections onto D are easy to compute. For this kind of “structured” geometric constraints (this explains the title of this paper), the entire method is then both an efficient tool and applicable to large-scale problems. In particular, we show that this is the case for MPCCs, optimization problems with cardinality constraints, and some rank-constrained matrix optimization problems.

The paper is organized as follows. We begin with restating some basic definitions from variational analysis in Sect. 2. There, we also relate the general regularity concept from [54] to the constraint qualification (the so-called relaxed constant positive linear dependence condition, RCPLD for short) used in the underlying paper [33] (as well as in many other related publications in this area). We then present the spectral gradient method for optimization problems over nonconvex sets in Sect. 3. This method is used to solve the resulting subproblems of our augmented Lagrangian method whose details are given in Sect. 4. Global convergence to M-type stationary points is also shown in this section. Since, in our augmented Lagrangian approach, we penalize the seemingly easy constraints $G(w) \in C$, but keep the condition $w \in D$ explicitly in the constraints, we have to compute projections onto D. Sect. 5 therefore considers a couple of situations where this can be done in a numerically very efficient way. Extensive computational experiments for some of these situations are documented in Sect. 6. This includes MPCCs, cardinality-constrained (sparse) optimization problems, and a rank-constrained reformulation of the famous MAXCUT problem. We close with some final remarks in Sect. 7.

Notation. The Euclidean inner product of two vectors $x,y\in {\mathbb {R}}^n$ will be denoted by $x^\top y$. More generally, ${\langle }x,y{\rangle }$ is used to represent the inner product of $x,y\in {\mathbb {W}}$ whenever ${\mathbb {W}}$ is some abstract Euclidean space. For brevity, we exploit $x+A:=A+x:=\left\{ x+a \,|\,a\in A\right\}$ for arbitrary vectors $x\in {\mathbb {W}}$ and sets $A\subset {\mathbb {W}}$. The sets ${\text {cone}}A$ and ${\text {span}}A$ denote the smallest cone containing the set A and the smallest subspace containing A, respectively. Whenever $L:{\mathbb {W}}\rightarrow {\mathbb {Y}}$ is a linear operator between Euclidean spaces ${\mathbb {W}}$ and ${\mathbb {Y}}$, $L^*:{\mathbb {Y}}\rightarrow {\mathbb {W}}$ denotes its adjoint. For some continuously differentiable mapping $\varphi :{\mathbb {W}}\rightarrow {\mathbb {Y}}$ and some point $w\in {\mathbb {W}}$, we use $\varphi '(w):{\mathbb {W}}\rightarrow {\mathbb {Y}}$ in order to denote the derivative of $\varphi$ at w which is a continuous linear operator. In the particular case ${\mathbb {Y}}:={\mathbb {R}}$, we set $\nabla \varphi (w):=\varphi '(w)^*1\in {\mathbb {W}}$ for brevity.

2 Preliminaries

We first recall some basic concepts from variational analysis in Sect. 2.1, and then introduce and discuss general stationarity and regularity concepts for the abstract problem (P) in Sect. 2.2.

2.1 Fundamentals of variational analysis

In this section, we comment on the tools of variational analysis which will be exploited in order to describe the geometry of the closed, convex set $C\subset {\mathbb {Y}}$ and the closed (but not necessarily convex) set $D\subset {\mathbb {W}}$ which appear in the formulation of (P).

The Euclidean projection $P_C :{\mathbb {Y}} \rightarrow {\mathbb {Y}}$ onto the closed, convex set C is given by

$$\begin{aligned} P_C (y) := \mathop {{{\,\mathrm{{\text {argmin}}}\,}}}\limits _{z \in C} \vert \vert z - y \vert \vert . \end{aligned}$$

Thus, the corresponding distance function $d_C :{\mathbb {Y}} \rightarrow {\mathbb {R}}$ can be written as

$$\begin{aligned} d_C (y) := \min _{z \in C} \vert \vert z - y \vert \vert = \vert \vert P_C(y) - y \vert \vert . \end{aligned}$$

On the other hand, projections onto the potentially nonconvex set D still exist, but are, in general, not unique. Therefore, we define the corresponding (usually set-valued) projection operator $\varPi _D :{\mathbb {W}} \rightrightarrows {\mathbb {W}}$ by

$$\begin{aligned} \varPi _D (x) := \mathop {{{\,\mathrm{{\text {argmin}}}\,}}}\limits _{z \in D} \vert \vert z - x \vert \vert \ne \varnothing . \end{aligned}$$

Given ${\bar{w}} \in D$, the closed cone

$$\begin{aligned} {\mathcal {N}}_D^lim ({\bar{w}}) := \limsup \limits _{w\rightarrow {\bar{w}}}\big [{\text {cone}}(w-\varPi _D(w))\big ] \end{aligned}$$

is referred to as the limiting normal cone to D at ${\bar{w}}$, see [59, 64] for other representations and properties of this variational tool. Above, we used the notion of the outer (or upper) limit of a set-valued mapping at a certain point, see e.g. [64, Definition 4.1]. For $w\notin D$, we set ${\mathcal {N}}_D^lim (w):=\varnothing$. Note that the limiting normal cone depends on the inner product of ${\mathbb {W}}$ and is stable in the sense that

$$\begin{aligned} \limsup \limits _{w \rightarrow {\bar{w}}} {\mathcal {N}}_D^lim (w) = {\mathcal {N}}_D^lim ({\bar{w}}) \qquad \forall {\bar{w}} \in {\mathbb {W}} \end{aligned}$$

(2.1)

holds. This stability property, which might be referred to as outer semicontinuity of the set-valued operator ${\mathcal {N}}_D^lim :{\mathbb {W}}\rightrightarrows {\mathbb {W}}$, will play an essential role in our subsequent analysis. The limiting normal cone to the convex set C coincides with the standard normal cone from convex analysis, i.e., for ${\bar{y}}\in C$, we have

$$\begin{aligned} {\mathcal {N}}_C^lim ({\bar{y}}) = {\mathcal {N}}_C ({\bar{y}}) := \left\{ \lambda \in {\mathbb {Y}} \,|\,{\langle }\lambda ,y-{\bar{y}}{\rangle } \le 0 \quad \forall y \in C \right\} . \end{aligned}$$

For points $y\notin C$, we set ${\mathcal {N}}_C(y):=\varnothing$ for formal completeness. Note that the stability property (2.1) is also satisfied by the set-valued operator ${\mathcal {N}}_C:{\mathbb {Y}}\rightrightarrows {\mathbb {Y}}$.

2.2 Stationarity and regularity concepts

Noting that the abstract set D is generally nonconvex in the exemplary settings we have in mind, the so-called concept of Mordukhovich-stationarity, which exploits limiting normals to D, is a reasonable concept of stationarity which addresses (P).

Definition 2.1

Let ${\bar{w}} \in {\mathbb {W}}$ be feasible for the optimization problem (P). Then ${\bar{w}}$ is called an M-stationary point (Mordukhovich-stationary point) of (P) if there exists a multiplier $\lambda \in {\mathbb {Y}}$ such that

$$\begin{aligned} 0 \in \nabla f({\bar{w}}) + G'({\bar{w}})^* \lambda + {\mathcal {N}}_D^lim ({\bar{w}}), \quad \lambda \in {\mathcal {N}}_C ( G({\bar{w}}) ). \end{aligned}$$

Note that this definition coincides with the usual KKT conditions of (P) if the set D is convex. An asymptotic counterpart of this definition is the following one, see [54].

Definition 2.2

Let ${\bar{w}} \in {\mathbb {W}}$ be feasible for the optimization problem (P). Then ${\bar{w}}$ is called an AM-stationary point (asymptotically M-stationary point) of (P) if there exist sequences $\{ w^k \},\{\varepsilon ^k\}\subset {\mathbb {W}}$ and $\{\lambda ^k\},\{ z^k \} \subset {\mathbb {Y}}$ such that $w^k\rightarrow {\bar{w}}$, $\varepsilon ^k\rightarrow 0$, $z^k\rightarrow 0$, as well as

$$\begin{aligned} \varepsilon ^k \in \nabla f(w^k) + G'(w^k)^* \lambda ^k + {\mathcal {N}}_D^lim (w^k), \quad \lambda ^k \in {\mathcal {N}}_C( G(w^k) - z^k) \qquad \forall k\in {\mathbb {N}}. \end{aligned}$$

The definition of an AM-stationary point is similar to the notion of an AKKT (asymptotic or approximate KKT) point in standard nonlinear programming, see [18], but requires some explanation: The meanings of the iterates $w^k$ and the Lagrange multiplier estimates $\lambda ^k$ should be clear. The vector $\varepsilon ^k$ measures the inexactness by which the stationary conditions are satisfied at $w^k$ and $\lambda ^k$. The vector $z^k$ does not occur (at least not explicitly) in the context of standard nonlinear programs, but is required here for the following reason: The method to be considered in this paper generates a sequence $\{ w^k \}$ satisfying $w^k \in D$, while the constraint $G(w) \in C$ gets penalized, hence, the condition $G(w^k) \in C$ will typically be violated. Consequently, the corresponding normal cone ${\mathcal {N}}_C ( G(w^k) )$ would be empty which is why we cannot expect to have $\lambda ^k \in {\mathcal {N}}_C ( G(w^k) )$, though we hope that this holds asymptotically. In order to deal with this situation, we therefore have to introduce the sequence $\{ z^k \}$. Let us note that AM-stationarity corresponds to so-called AKKT stationarity for conic optimization problems, i.e., where C is a closed, convex cone and $D:={\mathbb {W}}$, see [3, Section 5]. The more general situation where C and D are closed, convex sets and the overall problem is stated in arbitrary Banach spaces is investigated in [20]. Asymptotic notions of stationarity addressing situations where D is a nonconvex set of special type can be found, e.g., in [5, 46, 61]. As shown in [54], the overall concept of asymptotic stationarity can be further generalized to feasible sets which are given as the kernel of a set-valued mapping. Let us mention that the theory in this section is still valid in situations where C is merely closed. In this case, one may replace the normal cone to C in the sense of convex analysis by the limiting normal cone everywhere. However, for nonconvex sets C, our algorithmic approach from Sect. 4 is not valid anymore. Note that, for the price of a slack variable $w_s \in {\mathbb {Y}}$, we can transfer the given constraint system into

$$\begin{aligned} G(w)-w_s =0,\ (w_s ,w)\in C\times D \end{aligned}$$

where the right-hand side of the nonlinear constraint is trivially convex. In order to apply the algorithmic framework of this paper to this reformulation, projections onto C have to be computed efficiently. Moreover, there might be a difference between the asymptotic notions of stationarity and regularity discussed here when applied to this reformulation or the original formulation of the constraints.

Apart from the aforementioned difference, the motivation of AM-stationarity is similar to the one of AKKT-stationarity: Suppose that the sequence $\{ \lambda ^k \}$ is bounded and, therefore, convergent along a subsequence. Then, taking the limit on this subsequence in the definition of an AM-stationary point while using the stability property (2.1) of the limiting normal cone shows that the corresponding limit point satisfies the M-stationarity conditions from Definition 2.1. In general, however, the Lagrange multiplier estimates $\{ \lambda ^k \}$ in the definition of AM-stationarity might be unbounded. Though this boundedness can be guaranteed under suitable (relatively strong) assumptions, the resulting convergence theory works under significantly weaker conditions.

It is well known in optimization theory that a local minimizer of (P) is M-stationary only under validity of a suitable constraint qualification. In contrast, it has been pointed out in [54, Theorem 4.2, Section 5.1] that each local minimizer of (P) is AM-stationary. In order to infer that an AM-stationary point is already M-stationary, the presence of so-called asymptotic regularity is necessary, see [54, Definition 4.4].

Definition 2.3

A feasible point ${\bar{w}}\in {\mathbb {W}}$ of (P) is called AM-regular (asymptotically Mordukhovich-regular) whenever the condition

$$\begin{aligned} \limsup \limits _{w\rightarrow {\bar{w}},\,z\rightarrow 0}{\mathcal {M}}(w,z) \subset {\mathcal {M}}({\bar{w}},0) \end{aligned}$$

holds, where ${\mathcal {M}}:{\mathbb {W}}\times {\mathbb {Y}}\rightrightarrows {\mathbb {W}}$ is the set-valued mapping defined via

$$\begin{aligned} {\mathcal {M}}(w,z) := G'(w)^*{\mathcal {N}}_C(G(w)-z)+{\mathcal {N}}_D^lim (w). \end{aligned}$$

The concept of AM-regularity has been inspired by the notion of AKKT-regularity (sometimes referred to as cone continuity property), which became popular as one of the weakest constraint qualifications for standard nonlinear programs or MPCCs, see e.g. [7, 8, 61], and can be generalized to a much higher level of abstractness. In this regard, we would like to point the reader’s attention to the fact that AM-stationarity and -regularity from Definitions 2.2 and 2.3 are referred to as decoupled asymptotic Mordukhovich-stationarity and -regularity in [54] since these are already refinements of more general concepts. For the sake of a concise notation, however, we omit the term decoupled here.

It has been shown in [54, Section 5.1] that validity of AM-regularity at a feasible point ${\bar{w}}\in {\mathbb {W}}$ of (P) is implied by

$$\begin{aligned} 0\in G'({\bar{w}})^*\lambda +{\mathcal {N}}_D^lim ({\bar{w}}),\quad \lambda \in {\mathcal {N}}_C(G({\bar{w}})) \quad \Longrightarrow \quad \lambda = 0. \end{aligned}$$

(2.2)

The latter is known as NNAMCQ (no nonzero abnormal multiplier constraint qualification) or GMFCQ (generalized Mangasarian–Fromovitz constraint qualification) in the literature. Indeed, in the setting where we fix $C:={\mathbb {R}}^{m_1}_-\times \{0\}^{m_2}$ and $D:={\mathbb {W}}$, (2.2) boils down to the classical Mangasarian–Fromovitz constraint qualification from standard nonlinear programming. The latter choice for C will be of particular interest, which is why we formalize this setting below.

Setting 2.4

Given $m_1,m_2\in {\mathbb {N}}$, we set $m:=m_1+m_2$, ${\mathbb {Y}}:={\mathbb {R}}^{m}$, and $C:={\mathbb {R}}^{m_1}_-\times \{0\}^{m_2}$. No additional assumptions are postulated on the set D. We denote the component functions of G by $G_1,\ldots ,G_m:{\mathbb {W}}\rightarrow {\mathbb {R}}$. Thus, the constraint $G(w)\in C$ encodes the constraint system

$$\begin{aligned} G_i(w) \le 0\quad i=1,\ldots ,m_1,\qquad G_i(w) =0\quad i=m_1+1,\ldots ,m \end{aligned}$$

of standard nonlinear programming. For our analysis, we exploit the index sets

$$\begin{aligned} I({\bar{w}}):=\left\{ i\in \{1,\ldots ,m_1\} \,|\,G_i({\bar{w}})=0\right\} , \qquad J:=\{m_1+1,\ldots ,m\}, \end{aligned}$$

whenever ${\bar{w}}\in D$ satisfies $G({\bar{w}})\in C$ in the present situation.

Let us emphasize that we did not make any assumptions regarding the structure of the set D in Setting 2.4. Thus, it still covers numerous interesting problem classes like complementarity-, vanishing-, or switching-constrained programs. These so-called disjunctive programs of special type are addressed in the setting mentioned below which provides a refinement of Setting 2.4.

Setting 2.5

Let ${\mathbb {X}}$ be another Euclidean space, let $X\subset {\mathbb {X}}$ be the union of finitely many convex, polyhedral sets, and let $T\subset {\mathbb {R}}^2$ be the union of two polyhedrons $T_1,T_2\subset {\mathbb {R}}^2$. For functions $g:{\mathbb {X}}\rightarrow {\mathbb {R}}^{m_1}$, $h:{\mathbb {X}}\rightarrow {\mathbb {R}}^{m_2}$, and $p,q:{\mathbb {X}}\rightarrow {\mathbb {R}}^{m_3}$, we consider the constraint system given by

$$\begin{aligned} \begin{aligned} g_i(x)&\le 0{} & {} i=1,\ldots ,m_1,\\ h_i(x)&=0{} & {} i=1,\ldots ,m_2,\\ \big ( p_i(x),q_i(x) \big )&\in T{} & {} i=1,\ldots ,m_3,\\ x&\in X.{} & {} \end{aligned} \end{aligned}$$

Setting ${\mathbb {W}}:={\mathbb {X}}\times {\mathbb {R}}^{m_3}\times {\mathbb {R}}^{m_3}$, ${\mathbb {Y}}:={\mathbb {R}}^{m_1}\times {\mathbb {R}}^{m_2}\times {\mathbb {R}}^{m_3}\times {\mathbb {R}}^{m_3}$,

$$\begin{aligned} G(x,u,v):=\big (g(x),h(x),p(x)-u,q(x)-v\big ), \end{aligned}$$

and

$$\begin{aligned} C:={\mathbb {R}}^{m_1}_-\times \{0\}^{m_2+2m_3},\qquad D:=X\times {\widetilde{T}}, \end{aligned}$$

where we used ${\widetilde{T}}:=\left\{ (u,v) \,|\,(u_i,v_i)\in T\ \forall i\in \{1,\ldots ,m_3\}\right\}$, we can handle this situation in the framework of this paper.

Constraint regions as characterized in Setting 2.4 can be tackled with a recently introduced version of RCPLD (relaxed constant positive linear dependence constraint qualification), see [67, Definition 1.1].

Definition 2.6

Let ${\bar{w}}\in {\mathbb {W}}$ be a feasible point of the optimization problem (P) in Setting 2.4. Then ${\bar{w}}$ is said to satisfy RCPLD whenever the following conditions hold:

• (i) the family $(\nabla G_i(w))_{i\in J}$ has constant rank on a neighborhood of ${\bar{w}}$,

• (ii) there exists an index set $S\subset J$ such that the family $(\nabla G_i({\bar{w}}))_{i\in S}$ is a basis of the subspace ${\text {span}}\left\{ \nabla G_i({\bar{w}}) \,|\,i\in J\right\}$, and

• (iii) for each index set $I\subset I({\bar{w}})$, each set of multipliers $\lambda _i\ge 0$ ($i\in I$) and $\lambda _i\in {\mathbb {R}}$ ($i\in S$), not all vanishing at the same time, and each vector $\eta \in {\mathcal {N}}^lim _D({\bar{w}})$ which satisfy

  $$\begin{aligned} 0\in \sum _{i\in I\cup S}\lambda _i\nabla G_i({\bar{w}})+\eta , \end{aligned}$$

  we find neighborhoods U of ${\bar{w}}$ and V of $\eta$ such that for all $w\in U$ and ${\tilde{\eta }}\in {\mathcal {N}}^lim _D(w)\cap V$, the vectors from

  $$\begin{aligned} {\left\{ \begin{array}{ll} (\nabla G_i(w))_{i\in I\cup S},\,{\tilde{\eta }} &{} \text {if }{\tilde{\eta }} \ne 0,\\ (\nabla G_i(w))_{i\in I\cup S} &{} \text {if }{\tilde{\eta }} = 0 \end{array}\right. } \end{aligned}$$

  are linearly dependent.

RCPLD has been introduced for standard nonlinear programs (i.e., $D:={\mathbb {W}}={\mathbb {R}}^n$ in Setting 2.4) in [4]. Some extensions to complementarity-constrained programs can be found in [27, 34]. A more restrictive RCPLD-type constraint qualification which is capable of handling an abstract constraint set can be found in [35, Definition 1]. Let us note that RCPLD from Definition 2.6 does not depend on the precise choice of the index set S in (ii).

In case where D is a set of product structure, condition (iii) in Definition 2.6 can be slightly weakened in order to obtain a reasonable generalization of the classical relaxed constant positive linear dependence constraint qualification, see [67, Remark 1.1] for details. Observing that GMFCQ from (2.2) takes the particular form

$$\begin{aligned} 0\in \sum \limits _{i\in I({\bar{w}})\cup J}\lambda _i\nabla G_i({\bar{w}})+{\mathcal {N}}^lim _D({\bar{w}}), \quad \lambda _i\ge 0 \,(i\in I) \quad \Longrightarrow \quad \lambda _i=0\,(i\in I({\bar{w}})\cup J) \end{aligned}$$

in Setting 2.4, it is obviously sufficient for RCPLD. The subsequently stated result generalizes related observations from [7, 61].

Lemma 2.7

Let ${\bar{w}}\in {\mathbb {W}}$ be a feasible point for the optimization problem (P) in Setting 2.4 where RCPLD holds. Then ${\bar{w}}$ is AM-regular.

Proof

Fix some $\xi \in \limsup _{w\rightarrow {\bar{w}},\,z\rightarrow 0}{\mathcal {M}}(w,z)$. Then we find $\{w^k\},\{\xi ^k\}\subset {\mathbb {W}}$ and $\{z^k\}\subset {\mathbb {R}}^m$ which satisfy $w^k\rightarrow {\bar{w}}$, $\xi ^k\rightarrow \xi$, $z^k\rightarrow 0$, and $\xi ^k\in {\mathcal {M}}(w^k,z^k)$ for all $k\in {\mathbb {N}}$. Particularly, there are sequences $\{\lambda ^k\}$ and $\{\eta ^k\}$ satisfying $\lambda ^k\in {\mathcal {N}}_C(G(w^k)-z^k)$, $\eta ^k\in {\mathcal {N}}^lim _D(w^k)$, and $\xi ^k=G'(w^k)^*\lambda ^k+\eta _k$ for each $k\in {\mathbb {N}}$. From $G(w^k)-z^k\rightarrow G({\bar{w}})$ and the special structure of C, we find $G_i(w^k)-z^k_i<0$ for all $i\in \{1,\ldots ,m_1\}\setminus I({\bar{w}})$ and all sufficiently large $k\in {\mathbb {N}}$, i.e.,

$$\begin{aligned} \lambda ^k_i {\left\{ \begin{array}{ll} =0 &{} i\in \{1,\ldots ,m_1\}\setminus I({\bar{w}}),\\ \ge 0 &{} i\in I({\bar{w}}) \end{array}\right. } \end{aligned}$$

for sufficiently large $k\in {\mathbb {N}}$. Thus, we may assume without loss of generality that

$$\begin{aligned} \xi ^k=\sum \limits _{i\in I({\bar{w}})\cup J}\lambda ^k_i\nabla G_i(w^k)+\eta ^k \end{aligned}$$

holds for all $k\in {\mathbb {N}}$. By definition of RCPLD, $(\nabla G_i(w^k))_{i\in S}$ is a basis of the subspace ${\text {span}}\left\{ \nabla G_i(w^k) \,|\,i\in J\right\}$ for all sufficiently large $k\in {\mathbb {N}}$. Hence, there exist scalars $\mu ^k_i$ ($i\in S$) such that

$$\begin{aligned} \xi ^k = \sum \limits _{i\in I({\bar{w}})}\lambda ^k_i\nabla G_i(w^k) + \sum \limits _{i\in S}\mu ^k_i\nabla G_i(w^k) + \eta ^k \end{aligned}$$

holds for all sufficiently large $k\in {\mathbb {N}}$. On the other hand, [4, Lemma 1] yields the existence of an index set $I^k\subset I({\bar{w}})$ and multipliers ${\hat{\mu }}^k_i>0$ ($i\in I^k$), ${\hat{\mu }}^k_i\in {\mathbb {R}}$ ($i\in S$), and $\sigma _k\ge 0$ such that

$$\begin{aligned} \xi ^k = \sum \limits _{i\in I^k\cup S}{\hat{\mu }}^k_i\nabla G_i(w^k)+\sigma _k\eta ^k \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\sigma _k>0{} & {} \Longrightarrow{} & {} (\nabla G_i(w^k))_{i\in I^k\cup S},\,\eta ^k \text { linearly independent,}&\\&\sigma _k=0{} & {} \Longrightarrow{} & {} (\nabla G_i(w^k))_{i\in I^k\cup S} \text { linearly independent.}&\end{aligned} \end{aligned}$$

Since there are only finitely many subsets of $I({\bar{w}})$, there needs to exist $I\subset I({\bar{w}})$ such that $I^k=I$ holds along a whole subsequence. Along such a particular subsequence (without relabeling), we furthermore may assume $\sigma _k>0$ (otherwise, the proof will be easier) and, thus, may set ${\hat{\eta }}^k:=\sigma _k \eta ^k\in {\mathcal {N}}^lim _D(w^k)\setminus \{0\}$. From above, we find linear independence of

$$\begin{aligned} (\nabla G_i(w^k))_{i\in I\cup S},\,\hat{\eta }^k. \end{aligned}$$

Furthermore, we have

$$\begin{aligned} \xi ^k=\sum \limits _{i\in I\cup S}{\hat{\mu }}^k_i\nabla G_i(w^k)+{\hat{\eta }}^k. \end{aligned}$$

(2.3)

Suppose that the sequence $\{(({\hat{\mu }}^k_i)_{i\in I\cup S},{\hat{\eta }}^k)\}$ is not bounded. Dividing (2.3) by the norm of $(({\hat{\mu }}^k_i)_{i\in I\cup S},{\hat{\eta }}^k)$, taking the limit $k\rightarrow \infty$, and respecting boundedness of $\{\xi ^k\}$, continuity of $G'$, and outer semicontinuity of the limiting normal cone yield the existence of a non-vanishing multiplier $(({\hat{\mu }}_i)_{i\in I\cup S},{\hat{\eta }})$ which satisfies ${\hat{\mu }}_i\ge 0$ ($i\in I$), ${\hat{\eta }}\in {\mathcal {N}}^lim _D({\bar{w}})$, and

$$\begin{aligned} 0=\sum \limits _{i\in I\cup S}{\hat{\mu }}_i\nabla G_i({\bar{w}})+{\hat{\eta }}. \end{aligned}$$

Obviously, the multipliers ${\hat{\mu }}_i$ ($i\in I\cup S$) do not vanish at the same time since, otherwise, ${\hat{\eta }}=0$ would follow from above which yields a contradiction. Now, validity of RCPLD guarantees that the vectors

$$\begin{aligned} (\nabla G_i(w^k))_{i\in I\cup S},\,\hat{\eta }^k \end{aligned}$$

need to be linearly dependent for sufficiently large $k\in {\mathbb {N}}$. However, we already have shown above that these vectors are linearly independent, a contradiction.

Thus, the sequence $\{(({\hat{\mu }}^k_i)_{i\in I\cup S},{\hat{\eta }}^k)\}$ is bounded and, therefore, possesses a convergent subsequence with limit $(({\bar{\mu }}_i)_{i\in I\cup S},{\bar{\eta }})$. Taking the limit in (2.3) while respecting $\xi ^k\rightarrow \xi$, the continuity of $G'$, and the outer semicontinuity of the limiting normal cone, we come up with ${\bar{\mu }}_i\ge 0$ ($i\in I$), ${\bar{\eta }}\in {\mathcal {N}}^lim _D({\bar{w}})$, and

$$\begin{aligned} \xi =\sum \limits _{i\in I\cup S}{\bar{\mu }}_i\nabla G_i({\bar{w}})+{\bar{\eta }}. \end{aligned}$$

Finally, we set ${\bar{\mu }}_i:=0$ for all $i\in \{1,\ldots ,m\}\setminus (I\cup S)$. Then we have $({\bar{\mu }}_i)_{i=1,\ldots ,m}\in {\mathcal {N}}_C(G({\bar{w}}))$ from $I\subset I({\bar{w}})$, i.e.,

$$\begin{aligned} \xi \in G'({\bar{w}})^*{\mathcal {N}}_C(G({\bar{w}}))+{\mathcal {N}}^lim _D({\bar{w}}) ={\mathcal {M}}({\bar{w}},0). \end{aligned}$$

This shows that ${\bar{w}}$ is AM-regular. $\square$

A popular situation, where AM-regularity simplifies and, thus, becomes easier to verify, is described in the following lemma which follows from [54, Theorems 3.10, 5.2].

Lemma 2.8

Let ${\bar{w}}\in {\mathbb {W}}$ be a feasible point for the optimization problem (P) where C is a polyhedron and D is the union of finitely many polyhedrons. Then ${\bar{w}}$ is AM-regular if any only if

$$\begin{aligned} \limsup \limits _{w\rightarrow {\bar{w}}}\big (G'(w)^*{\mathcal {N}}_C(G({\bar{w}})) +{\mathcal {N}}_D^lim ({\bar{w}})\big ) \subset G'({\bar{w}})^*{\mathcal {N}}_C(G({\bar{w}}))+{\mathcal {N}}_D^lim ({\bar{w}}). \end{aligned}$$

Particularly, in case where G is an affine function, ${\bar{w}}$ is AM-regular.

Let us consider the situation where (P) is given as described in Setting 2.4, and assume in addition that $D:={\mathbb {W}}$ holds, i.e., that (P) is a standard nonlinear optimization problem with finitely many equality and inequality constraints. Then Lemma 2.8 shows that AM-regularity corresponds to the cone continuity property from [7, Definition 3.1], and the latter has been shown to be weaker than most of the established constraint qualifications which can be checked in terms of initial problem data.

The above lemma also helps us to find a tangible representation of AM-regularity in Setting 2.5.

Lemma 2.9

Let ${\bar{x}}\in {\mathbb {X}}$ be a feasible point of the optimization problem from Setting 2.5. Furthermore, define a set-valued mapping $\widetilde{{\mathcal {M}}}:{\mathbb {X}}\rightrightarrows {\mathbb {X}}$ by

$$\begin{aligned} \widetilde{{\mathcal {M}}}(x) := \left\{ {\mathfrak {L}}(x,\lambda ,\rho ,\mu ,\nu ,\xi ) \left| \begin{aligned}&0\le \lambda \perp g({\bar{x}}),\\&(\mu ,\nu )\in {\mathcal {N}}^lim _{{\widetilde{T}}}(p({\bar{x}}),q({\bar{x}})),\\&\xi \in {\mathcal {N}}^lim _X({\bar{x}}) \end{aligned}\right. \right\} \end{aligned}$$

where ${\mathfrak {L}}:{\mathbb {X}}\times {\mathbb {R}}^{m_1}\times {\mathbb {R}}^{m_2}\times {\mathbb {R}}^{m_3} \times {\mathbb {R}}^{m_3}\times {\mathbb {X}}\rightarrow {\mathbb {X}}$ is the function given by

$$\begin{aligned} {\mathfrak {L}}(x,\lambda ,\rho ,\mu ,\nu ,\xi ) := g'(x)^*\lambda +h'(x)^*\rho +p'(x)^*\mu +q'(x)^*\nu +\xi . \end{aligned}$$

Then the feasible point $({\bar{x}},p({\bar{x}}),q({\bar{x}}))$ of the associated problem (P) is AM-regular if and only if

$$\begin{aligned} \limsup \limits _{x\rightarrow {\bar{x}}}\widetilde{{\mathcal {M}}}(x) \subset \widetilde{{\mathcal {M}}}({\bar{x}}). \end{aligned}$$

(2.4)

Proof

First, observe that transferring the constraint region from Setting 2.5 into the form used in (P) and keeping Lemma 2.8 in mind shows that AM-regularity of $({\bar{x}},p({\bar{x}}),q({\bar{x}}))$ is equivalent to

$$\begin{aligned} \limsup \limits _{x\rightarrow {\bar{x}}}\widehat{{\mathcal {M}}}(x) \subset \widehat{{\mathcal {M}}}({\bar{x}}) \end{aligned}$$

(2.5)

where $\widehat{{\mathcal {M}}}:{\mathbb {X}}\rightrightarrows {\mathbb {X}}\times {\mathbb {R}}^{m_3}\times {\mathbb {R}}^{m_3}$ is given by

$$\begin{aligned} \widehat{{\mathcal {M}}}(x) := \left\{ \big ({\mathfrak {L}}(x,\lambda ,\rho ,{\tilde{\mu }},{\tilde{\nu }},\xi ), -{\tilde{\mu }}+\mu ,-{\tilde{\nu }}+\nu \big ) \left| \begin{aligned}&0\le \lambda \perp g({\bar{x}}),\\&(\mu ,\nu )\in {\mathcal {N}}^lim _{{\widetilde{T}}}(p({\bar{x}}),q({\bar{x}})),\\&\xi \in {\mathcal {N}}^lim _X({\bar{x}}) \end{aligned}\right. \right\} . \end{aligned}$$

Observing that $\eta \in \widetilde{{\mathcal {M}}}(x)$ is equivalent to $(\eta ,0,0)\in \widehat{{\mathcal {M}}}(x)$, (2.5) obviously implies (2.4). In order to show the converse relation, we assume that (2.4) holds and fix $(\eta ,\alpha ,\beta )\in \limsup _{x\rightarrow {\bar{x}}}\widehat{{\mathcal {M}}}(x)$. Then we find sequences $\{x^k\},\{\xi ^k\},\{\eta ^k\}\subset {\mathbb {X}}$, $\{\lambda ^k\}\subset {\mathbb {R}}^{m_1}$, $\{\rho ^k\}\subset {\mathbb {R}}^{m_2}$, and $\{\mu ^k\},\{{\tilde{\mu }}^k\},\{\nu ^k\},\{{\tilde{\nu }}^k\}\subset {\mathbb {R}}^{m_3}$ such that $x^k\rightarrow {\bar{x}}$, $\eta ^k\rightarrow \eta$, $-{\tilde{\mu }}^k+\mu ^k\rightarrow \alpha$, $-{\tilde{\nu }}^k+\nu ^k\rightarrow \beta$, and $\eta ^k={\mathfrak {L}}(x^k,\lambda ^k,\rho ^k,{\tilde{\mu }}^k,{\tilde{\nu }}^k,\xi ^k)$, $0\le \lambda ^k\perp g({\bar{x}})$, $(\mu ^k,\nu ^k)\in {\mathcal {N}}^lim _{{\widetilde{T}}}(p({\bar{x}}), q({\bar{x}}))$, as well as $\xi ^k\in {\mathcal {N}}^{lim }_X({\bar{x}})$ for all $k\in {\mathbb {N}}$. Setting $\alpha ^k:=-{\tilde{\mu }}^k+\mu ^k$ and $\beta ^k:=-{\tilde{\nu }}^k+\nu ^k$, we find $\eta ^k+p'(x^k)^*\alpha ^k+q'(x^k)^*\beta ^k={\mathfrak {L}}(x^k,\lambda ^k, \rho ^k,\mu ^k,\nu ^k,\xi ^k)$ for each $k\in {\mathbb {N}}$, and due to $\alpha ^k\rightarrow \alpha$ and $\beta ^k\rightarrow \beta$, validity of (2.4) yields $\eta +p'({\bar{x}})^*\alpha +q'({\bar{x}})^*\beta \in \widetilde{{\mathcal {M}}} ({\bar{x}})$, i.e., the existence of $\lambda \in {\mathbb {R}}^{m_1}$, $\rho \in {\mathbb {R}}^{m_2}$, $\mu ,\nu \in {\mathbb {R}}^{m_3}$, and $\xi \in {\mathbb {X}}$ such that $\eta +p'({\bar{x}})^*\alpha +q'({\bar{x}})^*\beta ={\mathfrak {L}}({\bar{x}}, \lambda ,\rho ,\mu ,\nu ,\xi )$, $0\le \lambda \perp g({\bar{x}})$, $(\mu ,\nu )\in {\mathcal {N}}^lim _{{\widetilde{T}}}(p({\bar{x}}),q({\bar{x}}))$, and $\xi \in {\mathcal {N}}^lim _X({\bar{x}})$. Thus, setting ${\tilde{\mu }}:=\mu -\alpha$ and ${\tilde{\nu }}:=\nu -\beta$, we find $(\eta ,\alpha ,\beta )\in \widehat{{\mathcal {M}}}({\bar{x}})$ showing (2.5). $\square$

Let us specify these findings for MPCCs which can be stated in the form (P) via Setting 2.5. Taking Lemmas 2.8 and 2.9 into account, AM-regularity corresponds to the so-called MPCC cone continuity property from [61, Definition 3.9]. The latter has been shown to be strictly weaker than MPCC-RCPLD, see [61, Definition 4.1, Theorem 4.2, Example 4.3] for a definition and this result. A similar reasoning can be used in order to show that problem-tailored versions of RCPLD associated with other classes of disjunctive programs are sufficient for the respective AM-regularity. This, to some extend, recovers our result from Lemma 2.7 although we need to admit that, exemplary, RCPLD from Definition 2.6 applied to MPCC in Setting 2.5 does not correspond to MPCC-RCPLD.

The above considerations underline that AM-regularity is a comparatively weak constraint qualification for (P). Exemplary, for standard nonlinear problems and for MPCCs, this follows from the above comments and the considerations in [7, 61]. For other types of disjunctive programs, the situation is likely to be similar, see e.g. [50, Figure 3] for the setting of switching-constrained optimization. It remains a topic of future research to find further sufficient conditions for AM-regularity which can be checked in terms of initial problem data, particularly, in situations where C and D are of particular structure like in semidefinite or second-order cone programming, see e.g. [6, Section 6]. Let us mention that the provably weakest constraint qualification which guarantees that local minimizers of a geometrically constrained program are M-stationary is slightly weaker than validity of the pre-image rule for the computation of the limiting normal cone to the constraint region of (P), see [34, Section 3] for a discussion, but the latter cannot be checked in practice. Due to [54, Theorem 3.16], AM-regularity indeed implies validity of this pre-image rule.

3 A spectral gradient method for nonconvex sets

In this section, we discuss a solution method for constrained optimization problems which applies whenever projections onto the feasible set are easy to find. Exemplary, our method can be used in situations where the feasible set has a disjunctive nonconvex structure.

To motivate the method, first consider the unconstrained optimization problem

$$\begin{aligned} \min _w \ \varphi (w)\quad \text {s.t.} \quad w \in {\mathbb {R}}^n \end{aligned}$$

with a continuously differentiable objective function $\varphi :{\mathbb {R}}^n \rightarrow {\mathbb {R}}$, and let $w^j$ be a current estimate for a solution of this problem. Computing the next iterate $w^{j+1}$ as the unique minimizer of the local quadratic model

$$\begin{aligned} \min _w \ \varphi (w^j) + \nabla \varphi (w^j)^\top (w - w^j) + \frac{\gamma _j}{2} \vert \vert w - w^j \vert \vert ^2 \end{aligned}$$

for some $\gamma _j > 0$ leads to the explicit expression

$$\begin{aligned} w^{j+1} := w^j - \frac{1}{\gamma _j} \nabla \varphi (w^j), \end{aligned}$$

i.e., we get a steepest descent method with stepsize $t_j := 1/\gamma _j$. Classical approaches compute $t_j$ using a suitable stepsize rule such that $\varphi (w^{j+1}) <\varphi (w^j)$. On the other hand, one can view the update formula as a special instance of a quasi-Newton scheme

$$\begin{aligned} w^{j+1} := w^j - B_j^{-1} \nabla \varphi (w^j) \end{aligned}$$

with the very simple quasi-Newton matrix $B_j := \gamma _j I$ as an estimate of the (not necessarily existing) Hessian $\nabla ^2\varphi (w^j)$. Then the corresponding quasi-Newton equation

$$\begin{aligned} B_{j+1} s^j = y^j \quad \text {with } s^j := w^{j+1} - w^j, \ y^j := \nabla \varphi (w^{j+1}) - \nabla \varphi (w^j), \end{aligned}$$

see [28], reduces to the linear system $\gamma _{j+1} s^j = y^j$. Solving this overdetermined system in a least squares sense, we then obtain the stepsize

$$\begin{aligned} \gamma _{j+1} := (s^j)^\top y^j / (s^j)^\top s^j \end{aligned}$$

introduced by Barzilai and Borwein [10]. This stepsize often leads to very good numerical results, but may not yield a monotone decrease in the function value. A convergence proof for general nonlinear programs is therefore difficult, even if the choice of $\gamma _j$ is safeguarded in the sense that it is projected onto some box $[ \gamma _{\min }, \gamma _{\max } ]$ for suitable constants $0< \gamma _{\min } < \gamma _{\max }$.

Raydan [62] then suggested to control this nonmonotone behavior by combining the Barzilai–Borwein stepsize with the nonmonotone linesearch strategy introduced by Grippo et al. [32]. This, in particular, leads to a global convergence theory for general unconstrained optimization problems.

This idea was then generalized by Birgin et al. [19] to constrained optimization problems

$$\begin{aligned} \min _w \ \varphi (w) \quad \text {s.t.} \quad w \in W \end{aligned}$$

with a nonempty, closed, and convex set $W\subset {\mathbb {R}}^n$ and is called the nonmonotone spectral gradient method. Here, we extend their approach to minimization problems

$$\begin{aligned} \min _w \ \varphi (w) \quad \text {s.t.} \quad w \in D \end{aligned}$$

(3.1)

with a continuously differentiable function $\varphi :{\mathbb {W}} \rightarrow {\mathbb {R}}$ and some nonempty, closed set $D\subset {\mathbb {W}}$, where ${\mathbb {W}}$ is an arbitrary Euclidean space. Let us emphasize that neither $\varphi$ nor D need to be convex in our subsequent considerations. A detailed description of the corresponding generalized spectral gradient is given in Algorithm 3.1.

Particular instances of this approach with nonconvex sets D can already be found in [13, 25, 26, 33]. Note that all iterates belong to the set D, that the subproblems ($Q (j,i)$) are always solvable, and that we have to compute only one solution, although their solutions are not necessarily unique. We would like to emphasize that $\nabla \varphi (w^j)$ was used in the formulation of ($Q (j,i)$) in order to underline that Algorithm 3.1 is a projected gradient method. Indeed, simple calculations reveal that the global solutions of ($Q (j,i)$) correspond to the projections of $w^j-\gamma _{j,i}^{-1}\nabla \varphi (w^j)$ onto D. Note also that the acceptance criterion in Line 8 is the nonmonotone Armijo rule introduced by Grippo et al. [32]. In particular, the parameter $m_j := \min (j,m)$ controls the nonmonotonicity. The choice $m = 0$ corresponds to the standard (monotone) method, whereas $m > 0$ typically allows larger stepsizes and often leads to faster convergence of the method.

We stress that the previous generalization of existing spectral gradient methods plays a fundamental role in order to apply our subsequent augmented Lagrangian technique to several interesting and difficult optimization problems, but the convergence analysis of Algorithm 3.1 can be carried out similar to the one given in [33] where a more specific situation is discussed. We therefore skip the corresponding proofs in this section, but for the reader’s convenience, we present them in Appendix A.

The goal of Algorithm 3.1 is the computation of a point which is approximately M-stationary for (3.1). We recall that w is an M-stationary point of (3.1) if

$$\begin{aligned} 0 \in \nabla \varphi (w) + {\mathcal {N}}_D^lim (w) \end{aligned}$$

holds, and that each locally optimal solution of (3.1) is M-stationary by [59, Theorem 6.1]. Similarly, since $w^{j,i}$ solves the subproblem (), it satisfies the corresponding M-stationarity condition

$$\begin{aligned} 0 \in \nabla \varphi (w^j) + \gamma _{j,i} \big ( w^{j,i} - w^j \big ) + {\mathcal {N}}_D^lim (w^{j,i}) . \end{aligned}$$

(3.2)

Let us point the reader’s attention to the fact that strong stationarity, where the limiting normal cone is replaced by the smaller regular normal cone in the stationarity system, provides a more restrictive necessary optimality condition for (3.1) and the surrogate ($Q (j,i)$), see [64, Definition 6.3, Theorem 6.12]. It is well known that the limiting normal cone is the outer limit of the regular normal cone. In contrast to the limiting normal cone, the regular one is not robust in the sense of (2.1), and since we are interested in taking limits later on, one either way ends up with a stationarity systems in terms of limiting normals at the end. Thus, we will rely on the limiting normal cone and the associated concept of M-stationarity.

For the following theoretical results, we neglect the termination criterion in Line 5. This means that Algorithm 3.1 does not terminate and performs either infinitely many inner or infinitely many outer interations. The first result analyzes the inner loop.

Proposition 3.1

Consider a fixed (outer) iteration j in Algorithm 3.1. Then the inner loop terminates (due to Line 8) or

$$\begin{aligned} \vert \vert \gamma _{j,i} \big ( w^j - w^{j,i} \big ) + \nabla \varphi (w^{j,i}) - \nabla \varphi (w^j) \vert \vert \rightarrow 0 \qquad \text {as}\quad i \rightarrow \infty . \end{aligned}$$

(3.3)

If the inner loop does not terminate, we get $w^{j,i} \rightarrow w^j$ and $w^j$ is M-stationary.

We refer to Appendix A for the proof. It remains to analyze the situation where the inner loop always terminates. Let $w^0 \in D$ be the starting point from Algorithm 3.1, and let

$$\begin{aligned} {\mathcal {S}}_\varphi (w^0) := \big \{ w \in D \,|\,\varphi (w) \le \varphi (w^0) \big \} \end{aligned}$$

denote the corresponding (feasible) sublevel set. Then the following observation holds, see [32, 66] and Appendix A for the details.

Proposition 3.2

We assume that the inner loop in Algorithm 3.1 always terminates (due to Line 8) and we denote by $\{ w^j \}$ the infinite sequence of (outer) iterates. Assume that $\varphi$ is bounded from below and uniformly continuous on ${\mathcal {S}}_\varphi (w^0)$. Then we have $\vert \vert w^{j+1} - w^j \vert \vert \rightarrow 0$ as $j \rightarrow \infty$.

The previous result allows to prove the following main convergence result for Algorithm 3.1, see, again, Appendix A for a complete proof.

Proposition 3.3

We assume that the inner loop in Algorithm 3.1 always terminates (due to Line 8) and we denote by $\{ w^j \}$ the infinite sequence of (outer) iterates. Assume that $\varphi$ is bounded from below and uniformly continuous on ${\mathcal {S}}_\varphi (w^0)$. Suppose that ${\bar{w}}$ is an accumulation point of $\{ w^j \}$, i.e., $w^j \rightarrow _K {\bar{w}}$ along a subsequence K. Then ${\bar{w}}$ is an M-stationary point of the optimization problem (3.1), and we have $\gamma _j \, \big ( w^{j+1} - w^j \big ) \rightarrow _K 0$.

From the proof of Proposition 3.2, it can be easily seen that the iterates of Algorithm 3.1 belong to the sublevel set ${\mathcal {S}}_\varphi (w^0)$ although the associated sequence of function values does not need to be monotonically decreasing. Hence, whenever this sublevel set is bounded, e.g., if $\varphi$ is coercive or if D is bounded, the existence of an accumulation point as in Proposition 3.3 is ensured. Moreover, the boundedness of ${\mathcal {S}}_\varphi (w^0)$ implies that this set is compact. Hence, $\varphi$ is automatically bounded from below and uniformly continuous on ${\mathcal {S}}_\varphi (w^0)$ in this situation.

By combining Propositions 3.1 and 3.3 we get the following convergence result.

Theorem 3.4

We consider Algorithm 3.1 without termination in Line 5 and assume that ${\mathcal {S}}_\varphi (w^0)$ is bounded. Then exactly one of the following situations occurs.

• (i) The inner loop does not terminate in the outer iteration j, $w^{j,i} \rightarrow w^j$ as $i \rightarrow \infty$, $w^j$ is M-stationary, and (3.3) holds.

• (ii) The inner loop always terminates. The infinite sequence $\{w^j\}$ of outer iterates possesses convergent subsequences $\{w^j\}_{K}$ and every convergent subsequence satisfies $w^j \rightarrow _K {\bar{w}}$, ${\bar{w}}$ is M-stationary, and $\gamma _j \, \big ( w^{j+1} - w^j \big ) \rightarrow _K 0$.

This result shows that the infinite sequence of (inner or outer) iterates of Algorithm 3.1 always converges towards M-stationary points (along subsequences). Note that the boundedness of ${\mathcal {S}}_\varphi (w^0)$ can be replaced by the assumptions on $\varphi$ of Proposition 3.3, but then the outer iterates $\{w^j\}$ might fail to possess accumulation points.

In what follows, we show that these theoretical results also give rise to a reasonable and applicable termination criterion which can be used in Line 5. To this end, we note that the optimality condition (3.2) is equivalent to

$$\begin{aligned} \gamma _{j,i} \big ( w^j - w^{j,i} \big ) + \nabla \varphi (w^{j,i}) - \nabla \varphi (w^j) \in \nabla \varphi (w^{j,i}) + {\mathcal {N}}_D^lim (w^{j,i}) . \end{aligned}$$

This motivates the usage of

$$\begin{aligned} \vert \vert \gamma _{j,i} \big ( w^j - w^{j,i} \big ) + \nabla \varphi (w^{j,i}) - \nabla \varphi (w^j) \vert \vert \le \varepsilon _{tol } \end{aligned}$$

(3.4)

(or a similar condition), with $\varepsilon _{tol } > 0$, as a termination criterion in Line 5. Indeed, Proposition 3.1 implies that the inner loop always terminates if (3.4) is used. Moreover, the termination criterion (3.4) directly encodes that $w^{j,i}$ is approximately M-stationary for (3.1). This is very desirable since the goal of Algorithm 3.1 is the computation of approximately M-stationary points.

Furthermore, we can check that condition (3.4) always ensures the finite termination of Algorithm 3.1 if the mild assumptions of Theorem 3.4 (or the even weaker assumptions of Proposition 3.3) are satisfied. Indeed, due to $\gamma _j = \gamma _{j,i_j}$ and $w^{j+1} = w^{j,i_j}$, we have $\gamma _{j,i_j} \big (w^{j} - w^{j,i_j}\big ) = \gamma _j \big (w^j - w^{j+1}\big ) \rightarrow _K 0$. Using $w^{j+1}, w^{j} \rightarrow _K {\bar{w}}$ and the continuity of $\nabla \varphi :{\mathbb {W}}\rightarrow {\mathbb {W}}$ shows $\nabla \varphi (w^{j,i_j}) - \nabla \varphi (w^j) = \nabla \varphi (w^{j+1}) - \nabla \varphi (w^j) \rightarrow _K 0$. Thus, the left-hand side of (3.4) with $i = i_j$ is arbitrarily small if $j \in K$ is large enough. Thus, Algorithm 3.1 with the termination criterion (3.4) terminates in finitely many steps.

Let us mention that the above convergence theory differs from the one provided in [25, 26] since no Lipschitzianity of $\nabla \varphi :{\mathbb {W}}\rightarrow {\mathbb {W}}$ is needed. In the particular setting of complementarity-constrained optimization, related results have been obtained in [33, Section 4]. Our findings substantially generalize the theory from [33] to arbitrary set constraints.

4 An augmented Lagrangian approach for structured geometric constraints

Sect. 4.1 contains a detailed statement of our augmented Lagrangian method applied to the general class of problems (P) together with several explanations. The convergence theory is then presented in Sect. 4.2.

4.1 Statement of the algorithm

We now consider the optimization problem (P) under the given smoothness and convexity assumptions stated there (recall that D is not necessarily convex). This section presents a safeguarded augmented Lagrangian approach for the solution of (P). The method penalizes the constraints $G(w) \in C$, but leaves the possibly complicated condition $w \in D$ explicitly in the constraints. Hence, the resulting subproblems that have to be solved in the augmented Lagrangian framework have exactly the structure of the (simplified) optimization problems discussed in Sect. 3.

To be specific, consider the (partially) augmented Lagrangian

$$\begin{aligned} {\mathcal {L}}_{\rho } (w, \lambda ) := f(w) + \frac{\rho }{2} d_C^2 \left( G(w) + \frac{\lambda }{\rho } \right) \end{aligned}$$

(4.1)

of (P), where $\rho > 0$ denotes the penalty parameter. Note that the squared distance function of a nonempty, closed, and convex set is always continuously differentiable, see e.g. [11, Corollary 12.30], which yields that ${\mathcal {L}}_{\rho } ( \cdot , \lambda )$ is a continuously differentiable mapping. Using the definition of the distance, we can alternatively write this (partially) augmented Lagrangian as

$$\begin{aligned} {\mathcal {L}}_{\rho } (w, \lambda ) = f(w) + \frac{\rho }{2} \bigg \Vert G(w) + \frac{\lambda }{\rho } - P_C \left( G(w) + \frac{\lambda }{\rho } \right) \bigg \Vert ^2. \end{aligned}$$

In order to control the update of the penalty parameter, we also introduce the auxiliary function

$$\begin{aligned} V_\rho (w, u) := \bigg \Vert G(w) - P_C \left( G(w) + \frac{u}{\rho } \right) \bigg \Vert . \end{aligned}$$

(4.2)

This function $V_\rho$ can also be used to obtain a meaningful termination criterion, see the discussion after (4.4) below. The overall method is stated in Algorithm 4.1.

Line 6 of Algorithm 4.1, in general, contains the main computational effort since we have to “solve” a constrained nonlinear program at each iteration. Due to the nonconvexity of this subproblem, we only require to compute an M-stationary point of this program. In fact, we allow the computation of an approximately M-stationary point, with the vector $\varepsilon ^{k+1}$ measuring the degree of inexactness. The choice $\varepsilon ^{k+1} = 0$ corresponds to an exact M-stationary point. Note that the subproblems arising in Line 6 have precisely the structure of the problem investigated in Sect. 3, hence, the spectral gradient method discussed there is a canonical candidate for the solution of these subproblems (note also that the objective function ${\mathcal {L}}_{\rho _k} ( \cdot , u^k)$ is once, but usually not twice continuously differentiable).

Note that Algorithm 4.1 is called a safeguarded augmented Lagrangian method due to the appearance of the auxiliary sequence $\{ u^k \}\subset U$ where U is a bounded set. In fact, if we would replace $u^k$ by $\lambda ^k$ in Line 6 of Algorithm 4.1 (and the corresponding subsequent formulas), we would obtain the classical augmented Lagrangian method. However, the safeguarded version has superior global convergence properties, see [18] for a general discussion and [48] for an explicit (counter-) example. In practice, $u^k$ is typically chosen to be equal to $\lambda ^k$ as long as this vector belongs to the set U, otherwise $u^k$ is taken as the projection of $\lambda ^k$ onto this set. In situations where ${\mathbb {Y}}$ is equipped with some (partial) order relation $\lesssim$, a typical choice for U is given by the box $[u_{\min },u_{\max }]:=\left\{ u\in {\mathbb {Y}} \,|\,u_min \lesssim u\lesssim u_max \right\}$ where $u_min ,u_max \in {\mathbb {Y}}$ are given bounds satisfying $u_min \lesssim u_max$.

In order to understand the update of the Lagrange multiplier estimate in Line 7 of Algorithm 4.1, recall that the augmented Lagrangian is differentiable, with its derivative given by

$$\begin{aligned} \nabla _w {\mathcal {L}}_{\rho } (w, \lambda ) = \nabla f(w) + \rho G'(w)^* \left[ G(w) + \frac{\lambda }{\rho } - P_C \left( G(w) + \frac{\lambda }{\rho } \right) \right] , \end{aligned}$$

see [11, Corollary 12.30] again. Hence, if we denote the usual (partial) Lagrangian of (P) by

$$\begin{aligned} {\mathcal {L}} (w, \lambda ) :=f(w) + {\langle }\lambda ,G(w){\rangle }, \end{aligned}$$

we obtain from Line 7 that

$$\begin{aligned} \nabla _w {\mathcal {L}}_{\rho _k} (w^{k+1}, u^k) = \nabla f(w^{k+1}) + G'(w^{k+1})^* \lambda ^{k+1} = \nabla _w {\mathcal {L}}(w^{k+1}, \lambda ^{k+1}) . \end{aligned}$$

(4.3)

This formula is actually the motivation for the precise update used in Line 7.

The particular updating rule in Lines 8 to 12 of Algorithm 4.1 is quite common, but other formulas might also be possible. In particular, one can use a different norm in the definition (4.2) of $V_\rho$. Exemplary, we exploited the maximum-norm for our experiments in Sect. 6 where ${\mathbb {W}}$ is a space of real vectors or matrices. Let us emphasize that increasing the penalty parameter $\rho _k$ based on a pure infeasibility measure does not work in Algorithm 4.1. One usually has to take into account both the infeasibility of the current iterate (w.r.t. the constraint $G(w) \in C$) and a kind of complementarity condition (i.e., $\lambda \in {\mathcal {N}}_C(G(w))$).

For the discussion of a suitable termination criterion, we define

$$\begin{aligned} z^{k} := G(w^{k}) - P_C \left( G(w^{k}) + \frac{u^{k-1}}{\rho _{k-1}} \right) . \end{aligned}$$

Using (4.3) and the update formula for $\lambda ^{k}$, Algorithm 4.1 ensures

$$\begin{aligned} \varepsilon ^{k}&\in \nabla f(w^{k}) + G'(w^{k})^* \lambda ^{k} + {\mathcal {N}}_D^lim (w^{k}), \end{aligned}$$

(4.4a)

$$\begin{aligned} \lambda ^{k}&\in {\mathcal {N}}_C(G(w^{k}) - z^{k}), \end{aligned}$$

(4.4b)

and this corresponds to the definition of AM-stationary points, see Definition 2.2. Thus, it is reasonable to require $\varepsilon ^{k} \rightarrow 0$ and to use

$$\begin{aligned} \vert \vert z^{k}\vert \vert = V_{\rho _{k-1}}(w^{k}, u^{k-1}) \le \varepsilon _{tol } \end{aligned}$$

(4.5)

for some $\varepsilon _{tol }>0$ as a termination criterion. In practical implementations of Algorithm 4.1, a maximum number of iterations should also be incorporated into the termination criterion.

4.2 Convergence

Throughout our convergence analysis, we assume implicitly that Algorithm 4.1 does not stop after finitely many iterations.

Like all penalty-type methods in the setting of nonconvex programming, augmented Lagrangian methods suffer from the drawback that they generate accumulation points which are not necessarily feasible for the given optimization problem (P). The following (standard) result therefore presents some conditions under which it is guaranteed that limit points are feasible.

Proposition 4.1

Each accumulation point ${\bar{w}}$ of a sequence $\{ w^k \}$ generated by Algorithm 4.1 is feasible for the optimization problem (P) if one of the following conditions holds:

• (a) $\{ \rho _k \}$ is bounded, or

• (b) there exists some $B \in {\mathbb {R}}$ such that ${\mathcal {L}}_{\rho _k} (w^{k+1}, u^k) \le B$ holds for all $k \in {\mathbb {N}}$.

Proof

Let ${\bar{w}}$ be an arbitrary accumulation point of $\{w^k\}$ and, say, $\{ w^{k+1} \}_{K}$ a corresponding subsequence with $w^{k+1}\rightarrow _K{\bar{w}}$.

We start with the proof under validity of condition (a). Since $\{ \rho _k \}$ is bounded, Lines 8 to 12 of Algorithm 4.1 imply that $V_{\rho _k}(w^{k+1}, u^k) \rightarrow 0$ for $k \rightarrow \infty$. This implies

$$\begin{aligned} d_C ( G(w^{k+1}) ) \le \bigg \Vert G(w^{k+1}) - P_C \left( G(w^{k+1}) + \frac{u^k}{\rho _k} \right) \bigg \Vert = V_{\rho _k} ( w^{k+1}, u^k) \rightarrow 0. \end{aligned}$$

A continuity argument yields $d_C ( G({\bar{w}}) ) = 0$. Since C is a closed set, this implies $G({\bar{w}}) \in C$. Furthermore, by construction, we have $w^{k+1} \in D$ for all $k \in {\mathbb {N}}$, so that the closedness of D also yields ${\bar{w}} \in D$. Altogether, this shows that ${\bar{w}}$ is feasible for the optimization problem (P).

Let us now prove the result in presence of (b). In view of (a), it suffices to consider the situation where $\rho _k \rightarrow \infty$. By assumption, we have

$$\begin{aligned} f(w^{k+1}) + \frac{\rho _k}{2} d_C^2 \left( G(w^{k+1}) + \frac{u^k}{\rho _k} \right) \le B \qquad \forall k \in {\mathbb {N}}. \end{aligned}$$

Rearranging terms yields

$$\begin{aligned} d_C^2 \left( G(w^{k+1}) + \frac{u^k}{\rho _k} \right) \le \frac{2 ( B - f(w^{k+1}) )}{\rho _k} \qquad \forall k \in {\mathbb {N}}. \end{aligned}$$

(4.6)

Taking the limit $k \rightarrow _K \infty$ in (4.6) and using the boundedness of $\{ u^k \}$, we obtain

$$\begin{aligned} d_C^2 \left( G({\bar{w}}) \right) = \lim _{k \rightarrow _K\infty } d_C^2 \left( G(w^{k+1}) + \frac{u^k}{\rho _k} \right) = 0 \end{aligned}$$

by a continuity argument. Similar to part (a), this implies feasibility of ${\bar{w}}$. $\square$

The two conditions (a) and (b) of Proposition 4.1 are, of course, difficult to check a priori. Nevertheless, in the situation where each iterate $w^{k+1}$ is actually a global minimizer of the subproblem in Line 6 of Algorithm 4.1 and w denotes any feasible point of the optimization problem (P), we have

$$\begin{aligned} {\mathcal {L}}_{\rho _k} (w^{k+1}, u^k) \le {\mathcal {L}}_{\rho _k} (w, u^k) \le f(w) + \frac{\vert \vert u^k \vert \vert ^2}{2 \rho _k} \le f(w) + \frac{\vert \vert u^k \vert \vert ^2}{2 \rho _0}\le B \end{aligned}$$

for some suitable constant B due to the boundedness of the sequence $\{ u^k \}$. The same argument also works if $w^{k+1}$ is only an inexact global minimizer.

The next result shows that, even in the case where a limit point is not necessarily feasible, it still contains some useful information in the sense that it is at least a stationary point for the constraint violation. In general, this is the best that one can expect.

Proposition 4.2

Suppose that the sequence $\{ \varepsilon ^k \}$ in Algorithm 4.1 is bounded. Then each accumulation point ${\bar{w}}$ of a sequence $\{ w^k \}$ generated by Algorithm 4.1 is an M-stationary point of the so-called feasibility problem

$$\begin{aligned} \min _w \tfrac{1}{2} d_C^2 ( G(w) ) \quad \text {s.t.} \quad w \in D. \end{aligned}$$

(4.7)

Proof

In view of Proposition 4.1, if $\{ \rho _k \}$ is bounded, then each accumulation point is a global minimum of the feasibility problem (4.7) and, therefore, an M-stationary point of this problem.

Hence, it remains to consider the case where $\{ \rho _k \}$ is unbounded, i.e., we have $\rho _k \rightarrow \infty$ as $k \rightarrow \infty$. In view of Lines 6 and 7 of Algorithm 4.1, see also (4.3), we have

$$\begin{aligned} \varepsilon ^{k+1} \in \nabla f(w^{k+1}) + G'(w^{k+1})^* \lambda ^{k+1} + {\mathcal {N}}_D^lim (w^{k+1}) \end{aligned}$$

with $\lambda ^{k+1}$ as in Line 7. Dividing this inclusion by $\rho _k$ and using the fact that ${\mathcal {N}}_D^lim (w^{k+1})$ is a cone, we therefore get

$$\begin{aligned}{} & {} \frac{\varepsilon ^{k+1}}{\rho _k}{ \in } \frac{\nabla f(w^{k+1})}{\rho _k} {+}G'(w^{k+1})^* \bigg [ G(w^{k+1}) {+} \frac{u^k}{\rho _k} {-} P_C \bigg ( G(w^{k+1}) {+} \frac{u^k}{\rho _k}\bigg ) \bigg ]{+} {\mathcal {N}}_D^lim (w^{k+1}). \end{aligned}$$

Now, let ${\bar{w}}$ be an accumulation point and $\{ w^{k+1} \}_K$ be a subsequence satisfying $w^{k+1}\rightarrow _K {\bar{w}}$. Then the sequences $\{ \varepsilon ^{k+1} \}_K$, $\{ u^k \}_K$, and $\{ \nabla f(w^{k+1}) \}_K$ are bounded. Thus, taking the limit $k \rightarrow _K \infty$ yields

$$\begin{aligned} 0 \in G'({\bar{w}})^* \big [ G({\bar{w}}) - P_C ( G({\bar{w}}) ) \big ] + {\mathcal {N}}_D^lim ({\bar{w}}) \end{aligned}$$

by the outer semicontinuity of the limiting normal cone. Since we also have ${\bar{w}} \in D$ and due to

$$\begin{aligned} \nabla \big ( \tfrac{1}{2} d_C^2 \circ G\big )({\bar{w}}) = G'({\bar{w}})^* \big [ G({\bar{w}}) - P_C ( G({\bar{w}}) ) \big ], \end{aligned}$$

see, once more, [11, Corollary 12.30], it follows that ${\bar{w}}$ is an M-stationary point of the feasibility problem (4.7). $\square$

We next investigate suitable properties of feasible limit points. The following may be viewed as the main observation in that respect and shows that any such accumulation point is automatically an AM-stationary point in the sense of Definition 2.2.

Theorem 4.3

Suppose that the sequence $\{ \varepsilon ^k \}$ in Algorithm 4.1 satisfies $\varepsilon ^k \rightarrow 0$. Then each feasible accumulation point ${\bar{w}}$ of a sequence $\{ w^k \}$ generated by Algorithm 4.1 is an AM-stationary point.

Proof

Let $\{ w^{k+1} \}_{K}$ denote a subsequence such that $w^{k+1}\rightarrow _K{\bar{w}}$. Define

$$\begin{aligned} s^{k+1} := P_C \left( G(w^{k+1} ) + \frac{u^k}{\rho _k} \right) \quad \text {and} \quad z^{k+1} := G ( w^{k+1} ) - s^{k+1} \end{aligned}$$

for each $k \in {\mathbb {N}}$. We claim that the four (sub-) sequences $\{ w^{k+1} \}_K, \{ z^{k+1} \}_K$, $\{ \varepsilon ^{k+1} \}_K$, and $\{ \lambda ^{k+1} \}_K$ generated by Algorithm 4.1 or defined in the above way satisfy the properties from Definition 2.2 and therefore show that ${\bar{w}}$ is an AM-stationary point. By construction, we have $w^{k+1}\rightarrow _K {\bar{w}}$ and $\varepsilon ^{k+1}\rightarrow _K 0$. Further, from Line 6 of Algorithm 4.1 and (4.3), we obtain

$$\begin{aligned}{} & {} \varepsilon ^{k+1} \in \nabla _w {\mathcal {L}}_{\rho _k} (w^{k+1}, u^k) + {\mathcal {N}}_D^lim (w^{k+1}) \\{} & {} \qquad \,\,\,\,= \nabla f(w^{k+1}) + G'(w^{k+1})^* \lambda ^{k+1} + {\mathcal {N}}_D^lim (w^{k+1}). \end{aligned}$$

Since  ${\mathcal {N}}_C(s^{k+1})$ is a cone, the relation between $P_C$ and ${\mathcal {N}}_C$ together with the definitions of $s^{k+1}, \lambda ^{k+1}$, and $z^{k+1}$ yield

$$\begin{aligned} \lambda ^{k+1} = \rho _k \left[ G(w^{k+1} ) + \frac{u^k}{\rho _k} - s^{k+1} \right] \in {\mathcal {N}}_C ( s^{k+1} ) = {\mathcal {N}}_C (G(w^{k+1}) - z^{k+1}) . \end{aligned}$$

Hence, it remains to show $z^{k+1}\rightarrow _K 0$. To this end, we consider two cases, namely whether $\{ \rho _k \}$ stays bounded or is unbounded. In the bounded case, Lines 8 to 12 of Algorithm 4.1 imply that $V_{\rho _k}(w^{k+1}, u^k) \rightarrow 0$ for $k \rightarrow \infty$. The corresponding definitions therefore yield

$$\begin{aligned} \vert \vert z^{k+1}\vert \vert = \vert \vert G(w^{k+1}) - s^{k+1}\vert \vert = V_{\rho _k}(w^{k+1}, u^k) \rightarrow 0 \quad \text {for } k \rightarrow _K \infty . \end{aligned}$$

On the other hand, if $\{ \rho _k \}$ is unbounded, we have $\rho _k \rightarrow \infty$. Since $\{ u^k \}$ is bounded by construction, the continuity of the projection operator together with the assumed feasibility of ${\bar{w}}$ implies

$$\begin{aligned} s^{k+1} = P_C \left( G(w^{k+1} ) + \frac{u^k}{\rho _k} \right) \rightarrow P_C (G ({\bar{w}}) ) =G({\bar{w}}) \quad \text {for } k \rightarrow _K \infty . \end{aligned}$$

Consequently, we obtain $z^{k+1} = G (w^{k+1}) - s^{k+1} \rightarrow _K 0$ also in this case. Altogether, this implies that ${\bar{w}}$ is AM-stationary. $\square$

We point out that the proof of Theorem 4.3 even shows the convergence $\vert \vert z^{k+1}\vert \vert = V_{\rho _k}(w^{k+1}, u^k) \rightarrow _K 0$, i.e., the stopping criterion (4.5) will be satisfied after finitely many steps.

Recalling that, by definition, each AM-stationary point of (P) which is AM-regular must already be M-stationary, we obtain the following corollary.

Corollary 4.4

Suppose that the sequence $\{\varepsilon ^k\}$ in Algorithm 4.1 satisfies $\varepsilon ^k\rightarrow 0$. Then each feasible and AM-regular accumulation point ${\bar{w}}$ of a sequence $\{w^k\}$ generated by Algorithm 4.1 is an M-stationary point.

Keeping our discussions after Lemma 2.9 in mind, this result generalizes [33, Theorem 3] which addresses a similar MPCC-tailored augmented Lagrangian method and exploits MPCC-RCPLD.

5 Realizations

Let k be a fixed iteration of Algorithm 4.1. For the (approximate) solution of the ALM-subproblem in Line 6 of Algorithm 4.1, we may use Algorithm 3.1. Recall that, given an outer iteration j of Algorithm 3.1, we need to solve the subproblem

$$\begin{aligned} \min _w \ {\mathcal {L}}_{\rho _k}(w^j,u^k) + {\langle } \nabla _w {\mathcal {L}}_{\rho _k}(w^j,u^k) , w-w^j {\rangle } + \frac{\gamma _{j,i}}{2} \vert \vert w - w^j \vert \vert ^2 \quad \text {s.t.} \quad w \in D \end{aligned}$$

with some given $w^j$ and $\gamma _{j,i} > 0$ in the inner iteration i of Algorithm 3.1. As pointed out in Sect. 3, the above problem possesses the same solutions as

$$\begin{aligned} \min _w \bigg \Vert w - \left( w^j - \frac{1}{\gamma _{j,i}} \nabla _w{\mathcal {L}}_{\rho _k}(w^j,u^k) \right) \bigg \Vert ^2 \quad \text {s.t.} \quad w \in D, \end{aligned}$$

i.e., we need to be able to compute elements of the (possibly multi-valued) projection $\varPi _D \big ( w^j - \frac{1}{\gamma _{j,i}} \nabla _w{\mathcal {L}}_{\rho _k}(w^j,u^k) \big )$. Boiling this requirement down to its essentials, we have to be in position to find projections of arbitrary points onto the set D in an efficient way. Subsequently, this will be discussed in the context of several practically relevant settings.

5.1 The disjunctive programming case

We consider (P) in the special Setting 2.5 with ${\mathbb {X}}:={\mathbb {R}}^n$ and $X:=[\ell ,u]$ where $\ell ,u\in {\mathbb {R}}^n$ satisfy $-\infty \le \ell _i<u_i\le \infty$ for $i=1,\ldots ,n$. Recall that the set D is given by

$$\begin{aligned} D = \left\{ (x,y,z) \in {\mathbb {R}}^n \times {\mathbb {R}}^{m_3} \times {\mathbb {R}}^{m_3} \,|\,x\in [\ell ,u],\,(y_i,z_i)\in T\quad \forall i\in \big \{1,\ldots ,m_3\right\} \big \}\quad \end{aligned}$$

(5.1)

in this situation. For given ${\bar{w}}=({\bar{x}},{\bar{y}},{\bar{z}})\in {\mathbb {R}}^n\times {\mathbb {R}}^{m_3}\times {\mathbb {R}}^{m_3}$, we want to characterize the elements of $\varPi _D({\bar{w}})$. Therefore, we consider the optimization problem

$$\begin{aligned} \min _w \ \tfrac{1}{2} \vert \vert w - {\bar{w}} \vert \vert ^2 \quad \text {s.t.} \quad w = (x,y,z) \in D. \end{aligned}$$

(5.2)

We observe that the latter can be decomposed into the n one-dimensional optimization problems

$$\begin{aligned} \min \limits _{x_i} \ \tfrac{1}{2} ( x_i - {\bar{x}}_i )^2 \quad \text {s.t.} \quad x_i \in [\ell _i,u_i], \end{aligned}$$

$i=1,\ldots ,n$, possessing the respective solution $P_{[\ell _i,u_i]}({\bar{x}}_i)$, as well as into $m_3$ two-dimensional optimization problems

$$\begin{aligned} \min \limits _{y_i,z_i} \ \tfrac{1}{2} ( y_i - {\bar{y}}_i )^2 + \tfrac{1}{2} ( z_i - {\bar{z}}_i )^2\quad \text {s.t.} \quad (y_i,z_i)\in T, \end{aligned}$$

(5.3)

$i=1,\ldots ,m_3$. Due to $T=T_1\cup T_2$, each of these problems on its own can be decomposed into the two two-dimensional subproblems

$j=1,2$. In most of the popular settings from disjunctive programming, ($\textrm{R}(i,j)$) can be solved with ease. By a simple comparison of the associated objective function values, we find the solutions of (5.3). Putting the solutions of the subproblems together, we find the solutions of (5.2), i.e., the elements of $\varPi _D({\bar{w}})$.

In the remainder of this section, we consider a particularly interesting instance of this setting where T is given by

$$\begin{aligned} T:=\left\{ (s,t) \,|\,s\in [\sigma _1,\sigma _2],\,t\in [\tau _1,\tau _2],\,st=0\right\} . \end{aligned}$$

(5.4)

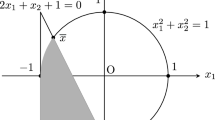
Here, $-\infty \le \sigma _1,\tau _1\le 0$ and $0<\sigma _2,\tau _2\le \infty$ are given constants. Particularly, we find the decomposition

$$\begin{aligned} T_1:=[\sigma _1,\sigma _2]\times \{0\},\qquad T_2:=\{0\}\times [\tau _1,\tau _2] \end{aligned}$$

of T in this case. Due to the geometrical shape of the set T, one might be tempted to refer to this setting as “box-switching constraints”. Note that it particularly covers

• switching constraints ($\sigma _1=\tau _1:=-\infty$, $\sigma _2=\tau _2:=\infty$), see [44, 57],

• complementarity constraints ($\sigma _1=\tau _1:=0$, $\sigma _2=\tau _2:=\infty$), see [52, 60], and

• relaxed reformulated cardinality constraints ($\sigma _1:=-\infty$, $\sigma _2:=\infty$, $\tau _1:=0$, $\tau _2:=1$), see [21, 23].

We refer the reader to Fig. 1 for a visualization of these types of constraints.

Fig. 1

Geometric illustrations of box-switching, switching, complementarity, and relaxed reformulated cardinality constraints (from left to right), respectively

One can easily check that the solutions of (R(i, 1)) and (R(i, 2)) are given by $(P_{[\sigma _1,\sigma _2]}({\bar{y}}_i),0)$ and $(0,P_{[\tau _1,\tau _2]}({\bar{z}}_i))$, respectively. This yields the following result.

Proposition 5.1

Consider the set D from (5.1) where T is given as in (5.4). For given ${\bar{w}} = ( {\bar{x}}, {\bar{y}}, {\bar{z}} ) \in {\mathbb {R}}^n\times {\mathbb {R}}^{m_3}\times {\mathbb {R}}^{m_3}$, we have ${\hat{w}}:= ({\hat{x}},{\hat{y}},{\hat{z}})\in \varPi _D({\bar{w}})$ if and only if ${\hat{x}}=P_{[\ell ,u]}({\bar{x}})$ and

$$\begin{aligned} ({\hat{y}}_i,{\hat{z}}_i) \in {\left\{ \begin{array}{ll} \{(P_{[\sigma _1,\sigma _2]}({\bar{y}}_i),0)\} &{}\text {if }\phi _s({\bar{y}}_i,{\bar{z}}_i)<\phi _t({\bar{y}}_i,{\bar{z}}_i),\\ \{(0,P_{[\tau _1,\tau _2]}({\bar{z}}_i))\} &{}\text {if }\phi _s({\bar{y}}_i,{\bar{z}}_i)>\phi _t({\bar{y}}_i,{\bar{z}}_i),\\ \{(P_{[\sigma _1,\sigma _2]}({\bar{y}}_i),0),(0,P_{[\tau _1,\tau _2]}({\bar{z}}_i))\} &{}\text {if }\phi _s({\bar{y}}_i,{\bar{z}}_i)=\phi _t({\bar{y}}_i,{\bar{z}}_i) \end{array}\right. } \end{aligned}$$

for all $i=1,\ldots ,m_3$, where we used

$$\begin{aligned} \phi _s(a,b):=(P_{[\sigma _1,\sigma _2]}(a)-a)^2+b^2, \qquad \phi _t(a,b):=a^2+(P_{[\tau _1,\tau _2]}(b)-b)^2. \end{aligned}$$

Particularly, it turns out that in order to compute the projections onto the set D under consideration, one basically needs to compute $n+2m_3$ projections onto real intervals. In the specific setting of complementarity-constrained programming, this already has been observed in [33, Section 4].

Let us briefly mention that other popular instances of disjunctive programs like vanishing- and or-constrained optimization problems, see e.g. [1, 55], where T is given by

$$\begin{aligned} T:=\left\{ (s,t) \,|\,st\le 0,\,t\ge 0\right\} \quad \text {or} \quad T:=\left\{ (s,t) \,|\,\min (s,t)\le 0\right\} , \end{aligned}$$

respectively, can be treated in an analogous fashion. Furthermore, an analogous procedure applies to more general situations where T is the union of finitely many convex, polyhedral sets.

5.2 The sparsity-constrained case

We fix ${\mathbb {W}}:={\mathbb {R}}^n$ and some $\kappa \in {\mathbb {N}}$ with $1\le \kappa \le n-1$. Consider the set

$$\begin{aligned} S_\kappa := \left\{ w \in {\mathbb {R}}^n \big | \vert \vert w \vert \vert _0 \le \kappa \right\} \end{aligned}$$

with $\vert \vert w \vert \vert _0$ being the number of nonzero entries of the vector w. This set plays a prominent role in sparse optimization and for problems with cardinality constraints. Since $S_\kappa$ is nonempty and closed, projections of some vector $w\in {\mathbb {R}}^n$ (w.r.t. the Euclidean norm) onto this set exist (but may not be unique), and are known to consist of those vectors $y\in {\mathbb {R}}^n$ such that the nonzero entries of y are precisely the $\kappa$ largest (in absolute value) components of w (which may not be unique), see e.g. [12, Proposition 3.6].

Hence, within our augmented Lagrangian framework, we may take $D := S_\kappa$ and then get an explicit formula for the solutions of the corresponding subproblems arising within the spectral gradient method. However, typical implementations of augmented Lagrangian methods (like ALGENCAN, see [2]) do not penalize box constraints, i.e., they leave the box constraints explicitly as constraints when solving the corresponding subproblems. Hence, let us assume that we have some lower and upper bounds satisfying $- \infty \le \ell _i < u_i \le \infty$ for all $i = 1, \ldots , n$. We are then forced to compute projections onto the set

$$\begin{aligned} D := S_\kappa \cap [\ell ,u]. \end{aligned}$$

(5.5)

It turns out that there exists an explicit formula for this projection. Before presenting the result, let us first assume, for notational simplicity, that

$$\begin{aligned} 0 \in [\ell _i,u_i] \qquad \forall i = 1, \ldots , n. \end{aligned}$$

(5.6)

We mention that this assumption is not restrictive. Indeed, let us assume that, e.g., $0 \not \in [\ell _1, u_1]$. Then the first component of $w \in D$ cannot be zero, and this shows

$$\begin{aligned} D = S_\kappa \cap [\ell , u] = [\ell _1, u_1] \times \big ( {\hat{S}}_{\kappa -1} \cap [{\hat{\ell }}, {\hat{u}}] \big ), \end{aligned}$$

(5.7)

where ${\hat{S}}_{\kappa -1} := \left\{ w \in {\mathbb {R}}^{n-1} \,|\,\vert \vert w\vert \vert _0 \le \kappa -1\right\}$ and the vectors ${\hat{\ell }}, {\hat{u}} \in {\mathbb {R}}^{n-1}$ are obtained from $\ell , u$ by dropping the first component, respectively. For the computation of the projection onto $S_\kappa$, we can now exploit the product structure (5.7). Similarly, we can remove all remaining components $i=2,\ldots ,n$ with $0 \not \in [\ell _i, u_i]$ from D. Thus, we can assume (5.6) without loss of generality.

We begin with a simple observation.

Lemma 5.2

Let $w \in {\mathbb {R}}^n$ be arbitrary. Then, for each $y\in \varPi _D(w)$, where D is the set from (5.5), we have

$$\begin{aligned} y_i \in \left\{ 0, P_{[\ell _i, u_i]}(w_i) \right\} \qquad \forall i = 1,\ldots , n . \end{aligned}$$

Proof

To the contrary, assume that $y_i \ne 0$ and $y_i \ne P_{[\ell _i, u_i]}(w_i)$ hold for some index $i\in \{1,\ldots ,n\}$. Define the vector $q \in {\mathbb {R}}^n$ by $q_j := y_j$ for $j \ne i$ and $q_i := P_{[\ell _i, u_i]}(w_i)$. Due to $y_i \ne 0$, we have $\vert \vert q\vert \vert _0 \le \vert \vert y\vert \vert _0\le \kappa$, i.e., $q \in S_\kappa$. Additionally, $q\in [\ell ,u]$ is clear from $y\in [\ell ,u]$ and $q_i=P_{[\ell _i,u_i]}(w_i)$. Thus, we find $q\in D$. Furthermore, $\vert \vert q - w\vert \vert < \vert \vert y - w\vert \vert$ since $q_i = P_{[\ell _i, u_i]}(w_i) \ne y_i$. This contradicts the fact that y is a projection of w onto D. $\square$

Due to the above lemma, we only have two choices for the value of the components associated with projections to D from (5.5). Thus, for an arbitrary index set $I \subset \left\{ 1,\ldots ,n\right\}$ and an arbitrary vector $w\in {\mathbb {R}}^n$, we define $p^I(w) \in {\mathbb {R}}^n$ via

$$\begin{aligned} p^I_i(w) := {\left\{ \begin{array}{ll} P_{[\ell _i,u_i]}(w_i) &{} \text {if } i \in I, \\ 0 &{} \text {otherwise} \end{array}\right. } \qquad \forall i=1,\ldots ,n. \end{aligned}$$

It remains to characterize those index sets I which ensure that $p^I(w)$ is a projection of w onto D. To this end, we define an auxiliary vector $d(w) \in {\mathbb {R}}^n$ via

$$\begin{aligned} d_i(w) := w_i^2 - \big ( P_{[\ell _i,u_i]} (w_i) - w_i \big )^2 \qquad \forall i = 1, \ldots , n. \end{aligned}$$

Note that this definition directly yields

$$\begin{aligned} \vert \vert p^I(w) - w\vert \vert ^2 = \vert \vert w\vert \vert ^2 - \sum _{i \in I} d_i(w) . \end{aligned}$$

(5.8)

We state the following simple observation.

Lemma 5.3

Fix $w \in {\mathbb {R}}^n$ and assume that (5.6) is valid. Then the following statements hold:

• (a) $d_i(w) \ge 0$ for all $i = 1, \ldots , n$,

• (b) $d_i(w) = 0 \Longleftrightarrow P_{[\ell _i,u_i]} (w_i) = 0$.

Proof

(a) Since $0 \in [\ell _i,u_i]$, we obtain

$$\begin{aligned} d_i(w) = ( w_i - 0 )^2 - \big ( w_i - P_{[\ell _i,u_i]} (w_i) \big )^2 \ge 0 \end{aligned}$$

by definition of the (one-dimensional) projection.

(b) If $P_{[\ell _i,u_i]} (w_i) = 0$ holds, we immediately obtain $d_i(w) = 0$. Conversely, let $d_i(w) = 0$. Then

$$\begin{aligned} 0 = w_i^2 - \big ( w_i - P_{[\ell _i,u_i]} (w_i) \big )^2 = P_{[\ell _i,u_i]} (w_i) \big ( 2 w_i - P_{[\ell _i,u_i]} (w_i) \big ). \end{aligned}$$

Hence, we find $P_{[\ell _i,u_i]} (w_i) = 0$ or $P_{[\ell _i,u_i]} (w_i) = 2 w_i$. In the first case, we are done. In the second case, we have $\left\{ 0, 2 w_i\right\} \subset [\ell _i, u_i]$. By convexity, this gives $w_i \in [\ell _i, u_i]$. Consequently, $w_i = P_{[\ell _i, u_i]}(w_i) = 2 w_i$. This implies $P_{[\ell _i, u_i]}(w_i) = 0$. $\square$

Observe that the second assertion of the above lemma implies

$$\begin{aligned} \vert \vert p^I(w)\vert \vert _0 = \left| \left\{ i \in I \,|\,P_{[\ell _i, u_i]} (w_i) \ne 0\right\} \right| = \left| \left\{ i \in I \,|\,d_i(w) \ne 0\right\} \right| \end{aligned}$$

(5.9)

for all $w\in {\mathbb {R}}^n$. This can be used to characterize the set of projections onto the set D from (5.5).

Proposition 5.4

Let D be the set from (5.5) and assume that (5.6) holds. Then, for each $w\in {\mathbb {R}}^n$, $y \in \varPi _D (w)$ holds if and only if there exists an index set $I \subset \{ 1, \ldots , n \}$ with $| I | = \kappa$ such that

$$\begin{aligned} d_i(w) \ge d_j(w) \qquad \forall i \in I, \ \forall j \not \in I \end{aligned}$$

(5.10)

and $y = p^I(w)$ hold.

Proof

If $y\in \varPi _D(w)$ holds, then $y = p^J(w)$ is valid for some index set J, see Lemma 5.2. Thus, it remains to check that $p^J(w)$ is a projection onto D if and only if $p^J(w) = p^I(w)$ holds for some index set I satisfying $\left| I\right| = \kappa$ and (5.10).

Note that $p^J(w)$ is a projection if and only if J minimizes $\vert \vert p^I(w) - w\vert \vert$ over all $I \subset \left\{ 1,\ldots ,n\right\}$ satisfying $\vert \vert p^I(w)\vert \vert _0 \le \kappa$. This can be reformulated via d(w) by using (5.8) and (5.9). In particular, $p^J(w)$ is a projection if and only if J solves

$$\begin{aligned} \max \limits _I \quad \sum _{i \in I} d_i(w) \quad \text {s.t.} \quad I \subset \left\{ 1,\ldots ,n\right\} , \quad \left| \left\{ i \in I \,|\,d_i(w) \ne 0\right\} \right| \le \kappa . \end{aligned}$$

(5.11)

It is clear that index sets I with $\left| I\right| = \kappa$ and (5.10) are solutions of this problem. This shows the direction $\Longleftarrow$.

To prove the converse direction $\Longrightarrow$, let $p^J(w)$ be a projection. Thus, J solves (5.11). We note that the solutions of this problem are invariant under addition and removal of indices i with $d_i(w) = 0$. Due to Lemma 5.3 (b), these operations also do not alter the associated $p^I(w)$. Thus, for each projection $p^J(w)$, we can add or remove indices i with $d_i(w) = 0$, to obtain a set I with $p^I(w) = p^J(w)$ and $\left| I\right| = \kappa$. It is also clear that (5.10) holds for such a choice of I. $\square$

Below, we comment on the result of Proposition 5.4.

Remark 5.5

• (a) Let $y=p^I(w)$ be a projection of $w\in {\mathbb {R}}^n$ onto D from (5.5) such that (5.6) holds. Observe that $y_i=0$ may also hold for some indices $i\in I$.

• (b) In the unconstrained case $[\ell ,u] = {\mathbb {R}}^n$, we find $d_i(w) = w_i^2$ for each $w\in {\mathbb {R}}^n$ and all $i=1,\ldots ,n$. Thus, Proposition 5.4 recovers the well-known characterization of the projection onto the set $S_\kappa$ which can be found in [12, Proposition 3.6].

We want to close this section with some brief remarks regarding the variational geometry of $D=S_\kappa \cap [\ell ,u]$ from (5.5). Observing that the sets $S_\kappa$ and $[\ell ,u]$ are both polyhedral in the sense that they can be represented as the union of finitely many polyhedrons, the normal cone intersection rule

$$\begin{aligned} {\mathcal {N}}^lim _D(w) = {\mathcal {N}}^lim _{S_\kappa \cap [\ell ,u]}(w) \subset {\mathcal {N}}^lim _{S_\kappa }(w)+{\mathcal {N}}^lim _{[\ell ,u]}(w) = {\mathcal {N}}^lim _{S_\kappa }(w)+{\mathcal {N}}_{[\ell ,u]}(w) \end{aligned}$$

applies for each $w\in D$ by means of [38, Corollary 4.2] and [63, Proposition 1]. While the evaluation of ${\mathcal {N}}_{[\ell ,u]}(w)$ is standard, a formula for ${\mathcal {N}}^lim _{S_\kappa }(w)$ can be found in [12, Theorem 3.9].

5.3 Low-rank approximation

5.3.1 General low-rank approximations

For natural numbers $m,n\in {\mathbb {N}}$ with $m,n\ge 2$, we fix ${\mathbb {W}}:={\mathbb {R}}^{m\times n}$. Equipped with the standard Frobenius inner product, ${\mathbb {W}}$ indeed is a Euclidean space. Now, for fixed $\kappa \in {\mathbb {N}}$ satisfying $1\le \kappa \le \min (m,n)-1$, let us investigate the set

$$\begin{aligned} D:=\left\{ W\in {\mathbb {W}} \,|\,{\text {rank}}W\le \kappa \right\} . \end{aligned}$$

Constraint systems involving rank constraints of type $W\in D$ can be used to model numerous practically relevant problems in computer vision, machine learning, computer algebra, signal processing, or model order reduction, see [53, Section 1.3] for an overview. Nowadays, one of the most popular applications behind low-rank constraints is the so-called low-rank matrix completion, particularly, the “Netflix-problem”, see [22] for details.

Observe that the variational geometry of D has been explored recently in [40]. Particularly, a formula for the limiting normal cone to this set can be found in [40, Theorem 3.1]. Using the singular value decomposition of a given matrix ${\widetilde{W}}\in {\mathbb {W}}$, one can easily construct an element of $\varPi _{D}({\widetilde{W}})$ by means of the so-called Eckart–Young–Mirsky theorem, see e.g. [53, Theorem 2.23].

Proposition 5.6

For a given matrix ${\widetilde{W}}\in {\mathbb {W}}$, let ${\widetilde{W}}=U\varSigma V^\top$ be its singular value decomposition with orthogonal matrices $U\in {\mathbb {R}}^{m\times m}$ and $V\in {\mathbb {R}}^{n\times n}$ as well as a diagonal matrix $\varSigma \in {\mathbb {R}}^{m\times n}$ whose diagonal entries are in non-increasing order. Let ${\widehat{U}}\in {\mathbb {R}}^{m\times \kappa }$ and ${\widehat{V}}\in {\mathbb {R}}^{n\times \kappa }$ be the matrices resulting from U and V by deleting the last $m-\kappa$ and $n-\kappa$ columns, respectively. Furthermore, let ${\widehat{\varSigma }}\in {\mathbb {R}}^{\kappa \times \kappa }$ be the top left $\kappa \times \kappa$ block of $\varSigma$. Then we have ${\widehat{U}}{\widehat{\varSigma }}\widehat{V}^\top \in \varPi _{D}({\widetilde{W}})$.

Note that the projection formulas from the previous sections allow a very efficient computation of the corresponding projections, which is in contrast to the projection provided by Proposition 5.6. Though the formula given there is conceptually very simple, its realization requires to compute the singular value decomposition of the given matrix.

5.3.2 Symmetric low-rank approximation

Given $n\in {\mathbb {N}}$ with $n\ge 2$, we consider the set of symmetric matrices ${\mathbb {W}}:={\mathbb {R}}^{n\times n}_{sym }$, still equipped with the Frobenius inner product. Now, for fixed $\kappa \in {\mathbb {N}}$ satisfying $1\le \kappa \le n$, let us investigate the set

$$\begin{aligned} D:=\left\{ W\in {\mathbb {W}} \,|\,W \succeq 0,\; {\text {rank}}W\le \kappa \right\} . \end{aligned}$$

Above, the constraint $W\succeq 0$ is used to abbreviate that W has to be positive semidefinite. Constraint systems involving rank constraints of type $W\in D$ arise frequently in several different mathematical models of data science, see [49] for an overview, and Sect. 6.3 for an application. Note that $\kappa :=n$ covers the setting of pure semidefiniteness constraints.

Exploiting the eigenvalue decomposition of a given matrix ${\widetilde{W}}\in {\mathbb {W}}$, one can easily construct an element of $\varPi _{D}({\widetilde{W}})$.

Proposition 5.7

For a given matrix ${\widetilde{W}}\in {\mathbb {W}}$, we denote by ${\widetilde{W}}= \sum _{i = 1}^n \lambda _i v_i v_i^\top$ its (orthonormal) eigenvalue decomposition with non-increasingly ordered eigenvalues $\lambda _1 \ge \lambda _2 \ge \ldots \ge \lambda _n$ and associated pairwise orthonormal eigenvectors $v_1,\ldots ,v_n$. Then we have ${\widehat{W}} := \sum _{i = 1}^\kappa \max (\lambda _i, 0) v_i v_i^\top \in \varPi _{D}({\widetilde{W}})$.

Proof

We define the positive and negative part ${\widetilde{W}}^\pm := \sum _{i = 1}^n \max (\pm \lambda _i, 0) v_i v_i^\top$. This yields ${\widetilde{W}} = {\widetilde{W}}^+ - {\widetilde{W}}^-$ and ${\langle }{\widetilde{W}}^+,{\widetilde{W}}^-{\rangle } = {\text {trace}}( {\widetilde{W}}^+ {\widetilde{W}}^-) = 0$. Thus, for each positive semidefinite $B \in {\mathbb {W}}$, we have

$$\begin{aligned} \vert \vert {\widetilde{W}} - B \vert \vert ^2 = \vert \vert {\widetilde{W}}^+ - B \vert \vert ^2 + \vert \vert {\widetilde{W}}^- \vert \vert ^2 + 2 {\langle }{\widetilde{W}}^-,B{\rangle } \ge \vert \vert {\widetilde{W}}^+ - B \vert \vert ^2 + \vert \vert {\widetilde{W}}^- \vert \vert ^2 . \end{aligned}$$

Since the singular value decomposition of ${\widetilde{W}}^+$ coincides with the eigenvalue decomposition, the right-hand side is minimized by $B = {\widehat{W}}$, see Proposition 5.6 while noting that we have ${\widehat{W}}={\widetilde{W}}^+$ in case $\kappa =n$. Due to ${\langle }{\widetilde{W}}^-,{\widehat{W}}{\rangle } = 0$, $B = {\widehat{W}}$ also minimizes the left-hand side. $\square$

It is clear that the computation of the $\kappa$ largest eigenvalues of ${\widetilde{W}}\in {\mathbb {W}}$ is sufficient to compute an element from the projection $\varPi _{D}({\widetilde{W}})$. This can be done particularly efficient for small $\kappa$ (note that $\kappa = 1$ holds in our application from Sect. 6.3).

5.4 Extension to nonsmooth objectives

For some lower semicontinuous functional $q:{\mathbb {W}}\rightarrow {\mathbb {R}}$, we consider the optimization problem

$$\begin{aligned} \min _w \ f(w)+q(w) \quad \text {s.t.} \quad G(w) \in C. \end{aligned}$$

(5.12)

Particularly, we do not assume that q is continuous. Exemplary, let us mention the special cases where q is the indicator function of a closed set, counts the nonzero entries of the argument vector (in case ${\mathbb {W}}:={\mathbb {R}}^n$), or encodes the rank of the argument matrix (in case ${\mathbb {W}}:={\mathbb {R}}^{m\times n}$). In this regard, (5.12) can be used to model real-world applications from e.g. image restoration or signal processing. Necessary optimality conditions and qualification conditions addressing (5.12) can be found in [35]. In [25], the authors suggest to handle (5.12) numerically with the aid of an augmented Lagrangian method (without safeguarding) based on the (partially) augmented Lagrangian function (4.1) and the subproblems

$$\begin{aligned} \min \limits _w \ {\mathcal {L}}_{\rho _k}(w,\lambda ^k)+q(w)\quad \text {s.t.}\quad w\in {\mathbb {W}} \end{aligned}$$

which are solved with a nonmonotone proximal gradient method inspired by [66]. In this regard, the solution approach to (5.12) described in [25] possesses some parallels to our strategy for the numerical solution of (P). The authors in [25] were able to prove convergence of their method to reasonable stationary points of (5.12) under a variant of the basic qualification condition and RCPLD. Let us mention that the authors in [25, 35] only considered standard inequality and equality constraints, but the theory in these papers can be easily extended to the more general constraints considered in (5.12) doing some nearby adjustments.

We note that (P) can be interpreted as a special instance of (5.12) where q plays the role of the indicator function of the set D. Then the nonmonotone proximal gradient method from [25] reduces to the spectral gradient method from Sect. 3. However, the authors in [25] did not challenge their method with discontinuous functionals q and, thus, cut away some of the more reasonable applications behind the model (P). Furthermore, we would like to mention that (5.12) can be reformulated (by using the epigraph ${\text {epi}}q:=\left\{ (w,\alpha ) \,|\,q(w)\le \alpha \right\}$ of q) as

$$\begin{aligned} \min \limits _{w,\alpha } \ f(w)+\alpha \quad \text {s.t.}\quad G(w)\in C,\ (w,\alpha )\in {\text {epi}}q \end{aligned}$$

(5.13)

which is a problem of type (P). One can easily check that (5.12) and (5.13) are equivalent in the sense that ${\bar{w}}\in {\mathbb {W}}$ is a local/global minimizer of (5.12) if and only if $({\bar{w}},q({\bar{w}}))$ is a local/global minimizer of (5.13). Problem (5.13) can be handled with Algorithm 4.1 as soon as the computation of projections onto $D := {\text {epi}}q$ is possible in an efficient way. Our result from Corollary 4.4 shows that Algorithm 4.1 applied to (5.13) computes M-stationary points of (5.12) under AM-regularity (associated with (5.13) at $({\bar{w}},q({\bar{w}}))$), i.e., we are in position to find points satisfying

$$\begin{aligned} 0\in \nabla f({\bar{w}})+\partial q({\bar{w}})+G'({\bar{w}})^*{\mathcal {N}}_C(G({\bar{w}})) \end{aligned}$$

under a very mild condition which enhances [25, Theorem 3.1]. Here, we used the limiting subdifferential of q given by

$$\begin{aligned} \partial q(w) := \big \{\xi \in {\mathbb {W}} \,|\,(\xi ,-1)\in {\mathcal {N}}_{{\text {epi}}q}^lim (w,q(w))\big \}. \end{aligned}$$

6 Numerical results

We implemented Algorithm 4.1, based on the underlying subproblem solver Algorithm 3.1, in MATLAB (R2021b) and tested it on three classes of difficult problems which are discussed in Sects. 6.1 to 6.3. All test runs use the following parameters:

$$\begin{aligned} \tau := 2,\, \sigma := 10^{-4},\, \beta := 10,\,\eta := 0.8,\, m := 10, \, \gamma _{\min } := 10^{-10}, \, \gamma _{\max } := 10^{10}. \end{aligned}$$

In iteration k of Algorithm 4.1, we terminate Algorithm 3.1 if the inner iterates $w^{j,i}$ satisfy

$$\begin{aligned} \vert \vert \gamma _{j,i} \big ( w^j - w^{j,i} \big ) + \nabla \varphi (w^{j,i}) - \nabla \varphi (w^j) \vert \vert _{\infty } \le \frac{10^{-4}}{\sqrt{k+1}}, \end{aligned}$$

where $\vert \vert \,\cdot \,\vert \vert _{\infty }$ stands for the maximum-norm for both ${\mathbb {W}}$ equal to ${\mathbb {R}}^n$ and equal to ${\mathbb {R}}^{n \times n}_{sym }$ (other Euclidean spaces do not occur in the subsequent applications), see (3.4). Similarly, we use the infinity norm in the definition (4.2) of $V_\rho$. Algorithm 4.1 is terminated as soon as (4.5) is satisfied with $\varepsilon _{tol } := 10^{-4}$. These two termination criteria ensure that the final iterate $w^{k}$ together with the multiplier $\lambda ^k$ is approximately M-stationary, see (4.4).

Given an arbitrary (possibly random) starting point $w^0$, we note that we first project this point onto the set D and then use this projected point as the true starting point, so that all iterates $w^k$ generated by Algorithm 4.1 belong to D. The choice of the initial penalty parameter is similar to the rule in [18, p. 153] and given by

$$\begin{aligned} \rho _0 := P_{[10^{-3}, 10^3]} \left( 10 \frac{\max ( 1, f(w^0) )}{\max \big ( 1, \tfrac{1}{2} d_C^2( G (w^0)) \big )} \right) . \end{aligned}$$

In all our examples, the space ${\mathbb {Y}}$ is given by ${\mathbb {R}}^m$ as in Setting 2.4. This allows us to choose the safeguarded multiplier estimate $u^k$ as the projection of the current value $\lambda ^k$ onto a given box $[u_{\min }, u_{\max }]$, where this box is (in componentwise fashion) chosen to be $[-10^{20},10^{20}]$ for all equality constraints and $[0,10^{20}]$ for all inequality constraints. In this way, we basically guarantee that the safeguarded augmented Lagrangian method from Algorithm 4.1 coincides with the classical approach as long as bounded multiplier estimates $\lambda ^k$ are generated.

6.1 MPCC examples

The specification of Algorithm 4.1 to MPCCs is essentially the method discussed in [33], where extensive numerical results (including comparisons with other methods) are presented. We therefore keep this section short and consider only two particular examples in order to illustrate certain aspects of our method.

Example 6.1

Here, for $w:=(y,z) \in {\mathbb {R}}^2$, we consider the two-dimensional MPCC given by

$$\begin{aligned} \min _w \tfrac{1}{2} (y-1)^2 + \tfrac{1}{2} (z-1)^2 \quad \text {s.t.} \quad y+z \le 2,\, y \ge 0,\, z \ge 0, y z = 0, \end{aligned}$$

which is essentially the example from [65] with an additional (inactive) inequality constraint in order to have at least one standard constraint, so that Algorithm 4.1 does not automatically reduce to the spectral gradient method. The problem possesses two global minimizers at (0, 1) and (1, 0) which are M-stationary (in fact, they are even strongly stationary in the MPCC-terminology). Moreover, it has a local maximizer at (0, 0) which is a point of attraction for many MPCC solvers since it can be shown to be C-stationary, see e.g. [39] for the corresponding definitions and some convergence results to C- and M-stationary points. Due to Lemma 2.8, each feasible point of the problem is AM-regular.

In view of our convergence theory, Algorithm 4.1 should not converge to the origin. To verify this statement numerically, we generated 1000 random starting points (uniformly distributed) from the box $[-10,10]^2$ and then applied Algorithm 4.1 to the above example. As expected, the method converges for all 1000 starting points to one of the two minima. Moreover, we can even start our method at the origin, and the method still converges to the point (1, 0) or (0, 1) . The limit point itself depends on our choice of the projection which is not unique for iterates $(y^k,z^k)$ with $y^k = z^k > 0$.

The next example is used to illustrate a limitation of our approach which is based on the fact that we exploit the spectral gradient method as a subproblem solver. There are examples where this spectral gradient method reduces the number of iterations even for two-dimensional problems from more than 100000 to just a few iterations. Nevertheless, in the end, the spectral gradient method is a projected gradient method, which exploits a different stepsize selection, but which eventually reduces to a standard projected gradient method if there are a number of consecutive iterations with very small progress, i.e., with almost identical function values during the last few iterations so that the maximum term in the nonmonotone line search is almost identical to the current function value used in the monotone version. This situation typically happens for problems which are ill-conditioned, and we illustrate this observation by the following example.

Example 6.2

We consider the optimal control of a discretized obstacle problem as investigated in [36, Section 7.4]. Using $w:=(x,y,z)$, in our notation, the problem is given by

$$\begin{aligned} \min _w{} & {} f(w) := \tfrac{1}{2} \vert \vert x \vert \vert ^2 - e^\top y + \tfrac{1}{2} \vert \vert y \vert \vert ^2 \\ \text {s.t.}{} & {} x \ge 0, \ -A y - x + z = 0, \ y \ge 0, \ z \ge 0, \ y^\top z = 0. \end{aligned}$$

Here, A is a tridiagonal matrix which arises from a discretization of the negative Laplace operator in one dimension, i.e., $a_{ii} = 2$ for all i and $a_{ij}= -1$ for all $i = j \pm 1$. Furthermore, e denotes the all-one vector of appropriate size. We note that ${\bar{w}}:=0$ is the global minimizer as well as an M-stationary point of this program. Again, Lemma 2.8 shows that each feasible point is AM-regular. Viewing the constraint $x \ge 0$ as a box constraint, taking a moderate discretization with $A \in {\mathbb {R}}^{64 \times 64}$, and using the all-one vector as a starting point, we obtain the results from Table 1. The number of (outer) iterations is denoted by k, j is the number of inner iterations, $j_{cum }$ the accumulated number of inner iterations, f-ev. provides the number of function evaluations (note that, due to the stepsize rule, we might have several function evaluations in a single inner iteration, hence, f-ev. is always an upper bound for $j_{cum }$), $f(w^k)$ denotes the current function value, the column titled “$V_k$” contains $V_{\rho _{k-1}}(w^k, u^{k-1})$, $t_j := 1/\gamma _j$ is the stepsize, and $\rho _k$ denotes the penalty parameter at iteration k.

The method terminates after 12 outer iterations, which is a reasonable number, especially taking into account that the final penalty parameter $\rho _k$ is relatively large, so that several subproblems with different values of $\rho _k$ have to be solved in the intermediate steps. On the other hand, the number of inner iterations j (at each outer iteration k) is very large. In the final step, the method requires more than one million inner iterations. This is a typical behavior of gradient-type methods and indicates that the underlying subproblems are ill-conditioned. This is also reflected by the fact that the stepsize $t_j$ tends to zero.

Table 1 Numerical results for Example 6.2

There are two types of difficulties in Example 6.2: there are challenging constraints (the complementarity constraints), and there is an ill-conditioning. The difficult constraints are treated by Algorithm 4.1 successfully, but the ill-conditioning causes some problems when solving the resulting subproblems. In principle, this difficulty can be circumvented by using another subproblem solver (like a semismooth Newton method, see [36]), but then it is no longer guaranteed that we obtain M-stationary points at the limit.

Despite the fact that the ill-conditioning causes some difficulties, we stress again that each iteration of the spectral gradient method is extremely cheap. Moreover, for all test problems in the subsequent sections, we put an upper bound of 50000 inner iterations (as a safeguard), and this upper bound was not reached in any of these examples.

6.2 Cardinality-constrained problems

We first consider an artificial example to illustrate the convergence behavior of Algorithm 4.1 for cardinality-constrained problems.

Example 6.3

Consider the example

$$\begin{aligned} \min _w \ f(w):=\tfrac{1}{2} w^\top Q w + c^\top w \quad \text {s.t.} \quad e^\top w\le 8, \ \vert \vert w \vert \vert _0 \le 2, \end{aligned}$$

where $Q := E + I$ with $E \in {\mathbb {R}}^{5 \times 5}$ being the all one matrix, $I \in {\mathbb {R}}^{5 \times 5}$ the identity matrix, and $c := - ( 3, 2, 3, 12, 5 )^\top \in {\mathbb {R}}^5$. Clearly, by Lemma 2.8, all feasible points are AM-regular. This is a minor modification of an example from [13], to which we added an (inactive) inequality constraint for the same reason as in Example 6.1. Taking into account that there are $\left( {\begin{array}{c}5\\ 2\end{array}}\right)$ possibilities to choose two possibly nonzero components of w, an elementary calculation shows that there are exactly 10 M-stationary points ${\bar{w}}^1, \ldots , {\bar{w}}^{10}$ which are given in Table 2 together with the corresponding function values. It follows that ${\bar{w}}^6$ is the global minimizer. The points ${\bar{w}}^3, {\bar{w}}^8$, and ${\bar{w}}^{10}$ have function values which are not too far away from $f({\bar{w}}^6)$, whereas all other M-stationary points have significantly larger function values. We then took 1000 random starting points from the box $[-10,10]^5$ (uniformly distributed) and applied Algorithm 4.1 to this example. Surprisingly, the method converged, for all 1000 starting points, to the global minimizer ${\bar{w}}^6$. We then changed the example by putting an upper bound $w_4\le 0$ to the fourth component. This excludes the four most interesting points ${\bar{w}}^3, {\bar{w}}^6, {\bar{w}}^8,$ and ${\bar{w}}^{10}$. Among the remaining points, the three vectors ${\bar{w}}^4, {\bar{w}}^7,$ and ${\bar{w}}^9$ have identical function values. Running our program again using 1000 randomly generated starting points, we obtain convergence to ${\bar{w}}^4$ in 589 cases, convergence to ${\bar{w}}^7$ in 350 situations, whereas in 61 instances only we observe convergence to the non-optimal point ${\bar{w}}^2$.

Table 2 M-stationary points and corresponding function values for Example 6.3

We next consider a class of cardinality-constrained problems of the form

$$\begin{aligned} \min _w \ \tfrac{1}{2} w^\top Q w \ \text { s.t. } \ \mu ^\top w \ge \varrho , \ e^\top w = 1, \ 0 \le w \le u, \ \vert \vert w \vert \vert _0 \le \kappa . \end{aligned}$$

(6.1)

This is a classical portfolio optimization problem, where Q and $\mu$ denote the covariance matrix and the mean of n possible assets, respectively, while $\varrho$ is some lower bound for the expected return. Furthermore, u provides an upper bound for the individual assets within the portfolio. The affine structure of the constraints in (6.1) implies that all feasible points are AM-regular, see Lemma 2.8. The data $Q, \mu , \varrho , u$ were randomly created by the test problem collection [30], which is available from the webpage https://commalab.di.unipi.it/datasets/MV/. Here, we used all 30 test instances of dimension $n := 200$ and three different values $\kappa \in \{ 5, 10, 20 \}$ for each problem. We apply three different methods:

• (a) Algorithm 4.1 with starting point $w^0 := 0$,

• (b) a boosted version of Algorithm 4.1, and

• (c) a CPLEX solver [41] to a reformulation of the portfolio optimization problem as a mixed integer quadratic program.

The CPLEX solver is used to (hopefully) identify the global optimum of the optimization problem (6.1). Note that we put a time limit of 0.5 hours for each test problem. Method (a) applies our augmented Lagrangian method to (6.1) using the set $D := \left\{ w \in [0,u]\, \,|\,\, \vert \vert w \vert \vert _0 \le \kappa \right\}$. Projections onto D are computed using the analytic formula from Proposition 5.4. Finally, the boosted version of Algorithm 4.1 is the following: We first delete the cardinality constraint from the portfolio optimization problem. The resulting quadratic program is then convex and can therefore be solved easily. Afterwards, we apply Algorithm 4.1 to a sequence of relaxations of (6.1) in which the cardinality is recursively decreased by 10 in each step (starting with $n - 10$) as long as the desired value $\kappa \in \left\{ 5, 10, 20\right\}$ is not undercut. For $\kappa =5$, a final call of Algorithm 4.1 with the correct cardinality is necessary since, otherwise, the procedure would terminate with cardinality level 10. In each outer iteration, the projection of the solution of the previous iteration onto the set D is used as a starting point.

Fig. 2

Optimal function values obtained by Algorithm 4.1 (red), Algorithm 4.1 with boosting technique (yellow), and CPLEX (blue), applied to the portfolio optimization problem (6.1) with cardinality $\kappa = 20$, $\kappa =10$, and $\kappa = 5$ (top to bottom)

The corresponding results are summarized in Fig. 2 for the three different values $\kappa \in \{5,10,20\}$. This figure compares the optimal function values obtained by the above three methods for each of the 30 test problems. The optimal function values produced by CPLEX are used here as a reference value in order to judge the quality of the results obtained by the other approaches. The main observations are the following: The optimal function value computed by CPLEX is (not surprisingly) always the best one. On the other hand, the corresponding values computed by method (a) are usually not too far away from the optimal ones. Moreover, for all test problems, the boosted version (b) generates even better function values which are usually very close to the ones computed by CPLEX. Of course, if $\kappa$ is taken smaller, the problems are getting more demanding and are therefore more difficult to solve (in general). Nevertheless, also for $\kappa = 5$, especially the boosted algorithm still computes rather good points. In this context, one should also note that our methods always terminate with a (numerically) feasible point, hence, the final iterate computed by our method can actually be used as a (good) approximation of the global minimizer. We also would like to mention that our MATLAB implementation of Algorithm 4.1 typically requires, on an Intel Core i7-8700 processor, only a CPU time of about 0.1 seconds for each of the test problems, whereas the boosted version requires roughly two seconds CPU time in average.

6.3 MAXCUT problems

This section considers the famous MAXCUT problem as an application of our algorithm to problems with rank constraints. To this end, let $G = (V, E)$ be an undirected graph with vertex set $V = \{ 1, \ldots , n \}$ and edges $e_{ij}$ between vertices $i , j \in V$. We assume that we have a weighted graph, with $a_{ij} = a_{ji}$ denoting the nonnegative weights of the edge $e_{ij}$. Since we allow zero weights, we can assume without loss of generality that G is a complete graph. Now, given a subset $S \subset V$ with complement $S^c$, the cut defined by S is the set $\delta (S) := \{ e_{ij} \,|\,i \in S, j \in S^c \}$ of all edges such that one end point belongs to S and the other one to $S^c$. The corresponding weight of this cut is defined by

$$\begin{aligned} w(S) := \sum _{e_{ij} \in \delta (S)} a_{ij} . \end{aligned}$$

The MAXCUT problem looks for the maximum cut, i.e., a cut with maximum weight. This graph-theoretical problem is known to be NP-hard, thus very difficult to solve.

Let $A := ( a_{ij} )$ and define $L:= {\text {diag}}(Ae) -A$. Then it is well known, see e.g. [31], that the MAXCUT problem can be reformulated as

$$\begin{aligned} \max _W \ \tfrac{1}{4} {\text {trace}}( L W ) \quad \text {s.t.} \quad {\text {diag}}W = e, \ W \succeq 0, \ {\text {rank}}W = 1, \end{aligned}$$

(6.2)

where the variable W is chosen from the space ${\mathbb {W}}:={\mathbb {R}}^{n \times n}_{sym }$. Due to the linear constraint ${\text {diag}}W = e$, it follows that this problem is equivalent to

$$\begin{aligned} \max _W \ \tfrac{1}{4} {\text {trace}}( L W ) \quad \text {s.t.} \quad {\text {diag}}W = e, \ W \succeq 0, \ {\text {rank}}W \le 1. \end{aligned}$$

(6.3)

Deleting the difficult rank constraint, one gets the (convex) relaxation

$$\begin{aligned} \max _W \ \tfrac{1}{4} {\text {trace}}( L W ) \quad \text {s.t.} \quad {\text {diag}}W = e, \ W \succeq 0, \end{aligned}$$

(6.4)

which is a famous test problem for semidefinite programs.

Here, we directly deal with (6.3) by taking $D: = \left\{ W\in {\mathbb {W}} \,|\,W \succeq 0, \ {\text {rank}}W \le 1 \right\}$ as the complicated set. Then GMFCQ holds at all feasible matrices of (6.3), see Appendix B. Particularly, AM-regularity is valid at all feasible points of (6.3). Projections onto D can be calculated via Proposition 5.7: Let $W \in {\mathbb {W}}$ denote an arbitrary symmetric matrix with maximum eigenvalue $\lambda$ and corresponding (normalized) eigenvector v (note that $\lambda$ and v are not necessarily unique), then $\max ( \lambda , 0 ) vv^\top$ is a projection of W onto D. In particular, the computation of this projection does not require the full spectral decomposition. However, it is not clear whether a projection onto the feasible set of (6.3) can be computed efficiently. Consequently, we penalize the linear constraint ${\text {diag}}W=e$ by the augmented Lagrangian approach.

Throughout this section, we take the zero matrix as the starting point. In order to illustrate the performance of our method, we begin with the simple graph from Fig. 3. Algorithm 4.1 applied to this example using the reformulation (6.3) (more precisely, the corresponding minimization problem) together with the previous specifications yields the iterations shown in Table 3. The meaning of the columns is the same as for Table 1.

Fig. 3

Example of a complete graph for the MAXCUT problem

Table 3 Numerical results for MAXCUT associated to the graph from Fig. 3

Note that the penalty parameter stays constant for this example. The feasibility measure tends to zero, and we terminate at iteration $k = 6$ since this measure becomes less than $10^{-4}$, i.e., we stop successfully. The associated function value is (approximately) 12 which actually corresponds to the maximum cut $S := \{ 1, 3 \}$ for the graph from Fig. 3, i.e., our method is able to solve the MAXCUT problem for this particular instance.

We next apply our method to two test problem collections that can be downloaded from http://biqmac.aau.at/biqmaclib.html, namely the rudy and the ising collection. The first class of problems consists of 130 instances, whereas the second one includes 48 problems. The optimal function value $f_{opt }$ of all these examples is known. The details of the corresponding results obtained by our method are given in [43]. Here, we summarize the main observations.

All $130 + 48$ test problems were solved successfully by our method since the standard termination criterion was satisfied after finitely many iterations, i.e., we stop with an iterate $W^k$ which is feasible (within the given tolerance). Hence, the corresponding optimal function value $f_{ALM }$ is a lower bound for the optimal value $f_{opt }$. For the sake of completeness, we also solved the (convex) relaxed problem from (6.4), using again our augmented Lagrangian method with $D := \left\{ W\in {\mathbb {W}} \,|\,W \succeq 0 \right\}$. The corresponding function value is denoted by $f_{SDP }$. Since the feasible set of (6.4) is larger than the one of (6.3), we have the inequalities $f_{ALM } \le f_{opt } \le f_{SDP }$. The corresponding details for the solution of the SDP-relaxation are provided in [43] for the rudy collection.

The bar charts from Figs. 4 and 5 summarize the results for the rudy and ising collections, respectively, in a very condensed way. They basically show that the function value $f_{ALM }$ obtained by our method is very close to the optimal value $f_{opt }$. More precisely, the interpretation is as follows: For each test problem, we take the quotient $f_{ALM } / f_{opt } \in [0,1]$. If this quotient is equal to, say, 0.91, we count this example as one where we reach $91 \%$ of the optimal function value. Figure 4 then says that all 130 test problems were solved with at least $88 \%$ of the optimal function value. There are still 106 test examples which are solved with a precision of at least $95 \%$. Almost one third of the test examples, namely 43 problems, are even solved with an accuracy of at least $99 \%$. For two examples (pm1d_80.9, and pw01_100.8), we actually get the exact global maximum.

Figure 5 has a similar meaning for the ising collection: Though there is no example which is solved exactly, almost one half of the problems reaches an accuracy of at least $99 \%$, and even in the worst case, we obtain a precision of $94 \%$.

Fig. 4

Summary of the results from the rudy collection

Fig. 5

Summary of the results from the ising collection

Altogether, this shows that we obtain a very good lower bound for the optimal function value. Moreover, since we are always feasible (in particular, all iterates are matrices of rank one), the final matrix can be used to create a cut through the given graph, i.e., the method provides a constructive way to create cuts which seem to be close to the optimal cuts. Note that this is in contrast to the semidefinite relaxation (6.4) which gives an upper bound, but the solution associated with this upper bound is usually not feasible for the MAXCUT problem since the rank constraint is violated (the results in [43] show that the solutions of the relaxed programs for the rudy collection are matrices of rank between 4 and 7). In particular, these matrices can, in general, not be used to compute a cut for the graph and, therefore, are less constructive than the outputs of our method. Moreover, it is interesting to observe that $f_{ALM }$ is usually much closer to $f_{opt }$ than $f_{SDP }$. In any case, both techniques together might be useful tools in a branch-and-bound-type method for solving MAXCUT problems.

7 Concluding remarks

In this paper, we demonstrated how M-stationary points of optimization problems with structured geometric constraints can be computed with the aid of an augmented Lagrangian method. The fundamental idea was to keep the complicated constraints out of the augmented Lagrangian function and to treat them directly in the associated subproblems which are solved by means of a nonmonotone projected gradient method. This way, the handling of challenging variational structures is encapsulated within the efficient computation of projections. This also puts a natural limit for the applicability. In contrast to several other approaches from the literature, the convergence guarantees for our method, which are valid in the presence of a comparatively weak asymptotic constraint qualification, remain true if the appearing subproblems are solved inexactly. Extensive numerical experiments visualized the quantitative qualities of this approach.

Despite our observations in Example 6.2, it might be interesting to think about extensions of these ideas to infinite-dimensional situations. In [20], an augmented Lagrangian method for the numerical solution of (P) in the context of Banach spaces has been considered where the set D was assumed to be convex, and the subproblems in the resulting algorithm are of the same type as in our paper. Furthermore, convergence of the method to KKT points was shown under validity of a problem-tailored version of asymptotic regularity. As soon as D becomes nonconvex, one has to face some uncomfortable properties of the appearing limiting normal cone which turns out to be comparatively large since weak-$*$-convergence is used for its definition as a set limit in the dual space, see [37, 58]. That it why the associated M-stationarity conditions are, in general, too weak in order to yield a reasonable stationarity condition. However, this issue might be surpassed by investigating the smaller strong limiting normal cone which is based on strong convergence in the dual space but possesses very limited calculus. It remains open whether reasonable asymptotic regularity conditions w.r.t. this variational object can be formulated. Furthermore, in order to exploit the smallness of the strong limiting normal cone in the resulting algorithm, one has to make sure (amongst others) that the (primal) sequence $\{w^k\}$ possesses strong accumulation points while the (dual) measures of inexactness $\{\varepsilon ^k\}$ need to be strongly convergent as well. This might be restrictive. Furthermore, it has to be clarified how the subproblems can be solved to approximate strong M-stationarity.

Appendices

Proofs

In this appendix, we provide the proofs which were left out in Sect. 3.

Proof of Proposition 3.1

Recall that $w^{j,i}$ is a solution of ($Q (j,i)$) with $\gamma _{j,i} = \tau ^{i-1} \gamma _j^0$. Since $w^j \in D$, the optimality of $w^{j,i}$ for ($Q (j,i)$) yields

$$\begin{aligned} {\langle }\nabla \varphi (w^j) , w^{j,i} - w^j {\rangle } + \frac{\gamma _{j,i}}{2} \vert \vert w^{j,i} - w^j \vert \vert ^2 \le 0 \qquad \forall i \in {\mathbb {N}}. \end{aligned}$$

(A.1)

The Cauchy–Schwarz inequality therefore gives

$$\begin{aligned} \frac{\gamma _{j,i}}{2} \vert \vert w^{j,i} - w^j \vert \vert \le \vert \vert \nabla \varphi (w^j) \vert \vert \qquad \forall i \in {\mathbb {N}}. \end{aligned}$$

This implies that $w^{j,i} \rightarrow w^j$ for $i \rightarrow \infty$. Now, we distinguish two cases. First, we consider that

$$\begin{aligned} \limsup _{i \rightarrow \infty } \gamma _{j,i} \vert \vert w^{j,i} - w^j \vert \vert > 0 . \end{aligned}$$

(A.2)

Hence, there exist a sequence $i_l \rightarrow \infty$ and a constant $\rho > 0$ such that

$$\begin{aligned} \gamma _{j,i_l} \vert \vert w^{j,i_l} - w^j \vert \vert \ge \rho \qquad \forall l\in {\mathbb {N}}. \end{aligned}$$

Consequently, we obtain from (A.1) that

$$\begin{aligned} \frac{\rho }{2} \vert \vert w^{j,i_l} - w^j \vert \vert \le \frac{\gamma _{j,i_l}}{2} \vert \vert w^{j,i_l} - w^j \vert \vert ^2 \le - {\langle }\nabla \varphi (w^j),w^{j,i_l} - w^j {\rangle } . \end{aligned}$$

Together with a Taylor expansion, we therefore get

$$\begin{aligned} \varphi \big ( w^{j,i_l}\big ) - \max _{r= 0, 1, \ldots , m_j}\varphi (w^{j-r})&\le \varphi \big ( w^{j,i_l}\big ) -\varphi (w^j) \\&= {\langle }\nabla \varphi (w^j), w^{j,i_l} - w^j {\rangle } + o \big ({ \vert \vert w^{j,i_l} - w^j \vert \vert }\big ) \\&\le \sigma {\langle }\nabla \varphi (w^j), w^{j,i_l} - w^j {\rangle } \end{aligned}$$

for all l sufficiently large, i.e., the inner loop terminates.

In the second case, (A.2) is not satisfied, i.e., $\gamma _{j,i} \vert \vert w^{j,i} - w^j \vert \vert \rightarrow 0$. By continuity of $\nabla \varphi$, this yields (3.3). Together with $w^{j,i} \rightarrow w^j$ and by using the continuity of $\nabla \varphi$ as well as (2.1) we can pass to the limit $i \rightarrow \infty$ in (3.2) and obtain that $w^j$ is M-stationary. $\square$

Proof of Proposition 3.2

Let $l(j)\in \{j-m_j,\ldots ,j\}$ be an index such that

$$\begin{aligned} \varphi (w^{l(j)}) = \max _{r= 0, 1, \ldots , m_j}\varphi (w^{j-r}) \qquad \forall j \in {\mathbb {N}}. \end{aligned}$$

Then the nonmonotone Armijo rule from Line 8 in Algorithm 3.1 can be rewritten as

$$\begin{aligned} \varphi (w^{j+1}) \le \varphi (w^{l(j)}) + \sigma {\langle }\nabla \varphi (w^j),w^{j+1} - w^j {\rangle }. \end{aligned}$$

(A.3)

Since $w^{j+1}$ solves

$$\begin{aligned} \min _w \ \varphi (w^j) + {\langle } \nabla \varphi (w^j) , w-w^j {\rangle } + \frac{\gamma _j}{2} \vert \vert w - w^j \vert \vert ^2 \quad \text {s.t.} \quad w \in D, \end{aligned}$$

(A.4)

we have

$$\begin{aligned} {\langle }\nabla \varphi (w^j) , w^{j+1} - w^j {\rangle } + \frac{\gamma _j}{2} \vert \vert w^{j+1} - w^j \vert \vert ^2 \le 0, \end{aligned}$$

i.e.,

$$\begin{aligned} {\langle }\nabla \varphi (w^j), w^{j+1} - w^j {\rangle } \le - \frac{\gamma _j}{2} \vert \vert w^{j+1} - w^j \vert \vert ^2 . \end{aligned}$$

Hence, (A.3) implies

$$\begin{aligned} \varphi (w^{j+1}) \le \varphi (w^{l(j)}) - \gamma _j \frac{\sigma }{2} \vert \vert w^{j+1} - w^j \vert \vert ^2 . \end{aligned}$$

(A.5)

We first note that the sequence $\{\varphi (w^{l(j)} ) \}_j$ is monotonically decreasing. Using $m_{j+1} \le m_j + 1$, this follows from

$$\begin{aligned} \varphi ( w^{l(j+1)} )&= \max _{r=0,1, \ldots , m_{j+1}}\varphi (w^{j+1-r}) \\&\le \max _{r=0,1, \ldots , m_j +1}\varphi (w^{j+1-r}) \\&= \max \left( \max _{r= 0, 1, \ldots , m_j}\varphi (w^{j-r}),\varphi (w^{j+1}) \right) \\&= \max \big (\varphi (w^{l(j)}),\varphi (w^{j+1}) \big ) \\&= \varphi (w^{l(j)}), \end{aligned}$$

where the last equality follows from (A.5). Since $\varphi$ is bounded from below, this implies

$$\begin{aligned} \lim _{j \rightarrow \infty }\varphi ( w^{l(j)} ) = \varphi ^* \end{aligned}$$

(A.6)

for some finite $\varphi ^*\in {\mathbb {R}}$. Applying (A.5) with j replaced by $l(j)-1$ and rearranging terms yields

$$\begin{aligned} \varphi (w^{l(j)}) -\varphi (w^{l(l(j)-1)}) \le - \gamma _{l(j)-1} \frac{\sigma }{2} \vert \vert w^{l(j)} - w^{l(j)-1} \vert \vert ^2 \le 0. \end{aligned}$$

Taking the limit $j \rightarrow \infty$ and using (A.6) therefore implies

$$\begin{aligned} \lim _{j \rightarrow \infty } \gamma _{l(j)-1} \vert \vert w^{l(j)} - w^{l(j)-1} \vert \vert ^2 = 0 . \end{aligned}$$

Since $\gamma _j \ge \gamma _{\min } > 0$ for all $j \in {\mathbb {N}}$, we get

$$\begin{aligned} \lim _{j \rightarrow \infty } d^{l(j)-1} = 0, \end{aligned}$$

(A.7)

where, for simplicity, we set $d^j := w^{j+1} - w^j$ for all $j \in {\mathbb {N}}$. Using (A.6) and (A.7), we then obtain

$$\begin{aligned} \varphi ^* = \lim _{j \rightarrow \infty }\varphi (w^{l(j)}) = \lim _{j \rightarrow \infty } \varphi \big ( w^{l(j)-1} + d^{l(j)-1} \big ) = \lim _{j \rightarrow \infty } \varphi (w^{l(j)-1}), \end{aligned}$$

(A.8)

where the last equality takes into account the uniform continuity of $\varphi$. We will now prove, by induction, that

$$\begin{aligned} \lim _{j \rightarrow \infty } d^{l(j)-r} = 0 \quad \text {and} \quad \lim _{j \rightarrow \infty }\varphi (w^{l(j)-r}) = \varphi ^* \quad \forall r\in {\mathbb {N}}. \end{aligned}$$

(A.9)

We already know from (A.7) and (A.8) that (A.9) holds for $r= 1$. Suppose that (A.9) holds for some $r\ge 1$. We need to show that it holds for $r+1$. Using (A.5) with j replaced by $l(j)-r-1$, we have

$$\begin{aligned} \varphi (w^{l(j)-r}) \le \varphi (w^{l(l(j)-r-1)}) - \gamma _{l(j)-r-1} \frac{\sigma }{2} \vert \vert d^{l(j)-r-1} \vert \vert ^2 \end{aligned}$$

(here we assume implicitly that j is large enough such that no negative indices $l(j)-r-1$ occur). Rearranging this expression and using $\gamma _j \ge \gamma _{\min }$ for all j yields

$$\begin{aligned} \vert \vert d^{l(j)-r-1} \vert \vert ^2 \le \frac{2}{\gamma _{\min } \sigma } \big (\varphi (w^{l(l(j)-r-1)}) -\varphi (w^{l(j)-r}) \big ) . \end{aligned}$$

Taking the limit $j \rightarrow \infty$ while using (A.6) as well as the induction hypothesis, it follows that

$$\begin{aligned} \lim _{j \rightarrow \infty } d^{l(j)-r-1} = 0, \end{aligned}$$

(A.10)

which proves the induction step for the first limit in (A.9). The second limit follows from

$$\begin{aligned} \lim _{j \rightarrow \infty } \varphi \big ( w^{l(j)-(r+1)} \big ) = \lim _{j \rightarrow \infty } \varphi \big ( w^{l(j)-(r+1)} + d^{l(j)-(r+1)} \big ) = \lim _{j \rightarrow \infty } \varphi \big ( w^{l(j)-r} \big ) = \varphi ^*, \end{aligned}$$

where the first equation follows from (A.10) together with the uniform continuity of $\varphi$, whereas the final equation is the induction hypothesis.

In the final step of our proof, we now show that $\lim _{j \rightarrow \infty } d^j = 0$. Suppose that this is not true. Then there is a (suitably shifted, for notational simplicity) subsequence $\{ d^{j-m-1} \}_K$ and a constant $\rho > 0$ such that

$$\begin{aligned} \vert \vert d^{j-m-1} \vert \vert \ge \rho \qquad \forall j \in K. \end{aligned}$$

(A.10)

Now, for each $j \in K$, the corresponding index l(j) is one of the indices $j - m, j - m + 1, \ldots , j$. Hence, we can write $j - m - 1 = l(j) - r_j$ for some index $r_j \in \{ 1, 2, \ldots , m+1 \}$. Since there are only finitely many possible indices $r_j$, we may assume without loss of generality that $r_j = r$ holds for some fixed index $r$. Then (A.9) implies

$$\begin{aligned} \lim _{j \rightarrow _K \infty } d^{j-m-1} = \lim _{j \rightarrow _K \infty } d^{l(j) - r} = 0. \end{aligned}$$

This contradicts (A.10) and therefore completes the proof. $\square$

Proof of Proposition 3.3

Let ${\bar{w}}$ be an arbitrary accumulation point, and let $\{ w^j \}_K$ be a subsequence such that $w^j\rightarrow _K{\bar{w}}$.

We start by showing $\gamma _j \, \big (w^{j+1} - w^j\big ) \rightarrow _K 0$. In the case that $\{ \gamma _j \}_K$ is bounded, this follows from Proposition 3.2. In the case that $\{ \gamma _j \}_K$ is unbounded, we find a subsequence $K' \subset K$ with $\gamma _j \rightarrow _{K'} \infty$ and $\gamma _j > \gamma _{\max }$ for all $j \in K'$. Then ${\hat{\gamma }}_j := \gamma _j / \tau = \tau ^{i_j - 1} \gamma _j^0 = \gamma _{j,i_j - 1}$ also converges to infinity. Due to $\gamma _j > \gamma _{\max }$, we have $i_j > 0$. Therefore, ${\hat{w}}^{j+1} := w^{j,i_j - 1}$ (which solves ($Q (j,i_j-1)$)) violates the nonmonotone Armijo-type condition from Line 8 in Algorithm 3.1, i.e., we have

$$\begin{aligned} \varphi \big ( {\hat{w}}^{j+1} \big ) > \max _{r= 0, 1, \ldots , m_j} \varphi ( w^{j-r} ) + \sigma {\langle }\nabla \varphi (w^j), {\hat{w}}^{j+1} - w^j {\rangle } \end{aligned}$$

(A.12)

for all $j \in K'$ sufficiently large. We now argue similar to the proof of Proposition 3.1 (except that j is not fixed now). Since ${\hat{w}}^{j+1}$ solves the subproblem ($Q (j,i_j-1)$), we obtain

$$\begin{aligned} {\langle }\nabla \varphi ( w^j ) ,{\hat{w}}^{j+1} - w^j {\rangle } + \frac{{\hat{\gamma }}_j}{2} \vert \vert {\hat{w}}^{j+1} - w^j \vert \vert ^2 \le 0, \end{aligned}$$

(A.13)

which implies that

$$\begin{aligned} \frac{{\hat{\gamma }}_j}{2} \vert \vert {\hat{w}}^{j+1} - w^j \vert \vert \le \vert \vert \nabla \varphi ( w^j ) \vert \vert . \end{aligned}$$

Since $w^j \rightarrow _{K'} {\bar{w}}$, this yields ${\hat{w}}^{j+1} - w^j \rightarrow _{K'} 0$. Hence, we also get ${\hat{w}}^{j+1} \rightarrow _{K'} {\bar{w}}$. For each $j\in {K'}$, the mean value theorem yields the existence of $\xi ^j$ on the line segment between ${\hat{w}}^{j+1}$ and $w^j$ such that

$$\begin{aligned} \varphi \big ( {\hat{w}}^{j+1} \big ) -\varphi (w^j) = {\langle }\nabla \varphi (\xi ^j), {\hat{w}}^{j+1} - w^j {\rangle }. \end{aligned}$$

Due to ${\hat{w}}^{j+1}, w^j \rightarrow _{K'} {\bar{w}}$, we find $\nabla \varphi (\xi ^j)-\nabla \varphi (w^j)\rightarrow _{K'} 0$. Using (A.12), we get

$$\begin{aligned} \sigma {\langle }\nabla \varphi (w^j) , {\hat{w}}^{j+1} - w^j {\rangle }&< \varphi \big ( {\hat{w}}^{j+1} \big ) - \max _{r= 0, 1, \ldots , m_j} \varphi ( w^{j-r} ) \\&\le \varphi \big ( {\hat{w}}^{j+1} \big ) - \varphi ( w^{j} ) \\&\le {\langle }\nabla \varphi (w^j), {\hat{w}}^{j+1} - w^j {\rangle } \\&\quad \quad + \vert \vert \nabla \varphi (\xi ^j) - \nabla \varphi (w^j) \vert \vert \, \vert \vert {\hat{w}}^{j+1} - w^j \vert \vert . \end{aligned}$$

Together with (A.13), we achieve

$$\begin{aligned} \frac{{\hat{\gamma }}_j}{2} \vert \vert {\hat{w}}^{j+1} - w^j \vert \vert ^2{} & {} \le -{\langle }\nabla \varphi ( w^j ) ,{\hat{w}}^{j+1} - w^j {\rangle } \\{} & {} \le \frac{\vert \vert \nabla \varphi (\xi ^j) - \nabla \varphi (w^j) \vert \vert }{1-\sigma } \vert \vert {\hat{w}}^{j+1} - w^j \vert \vert . \end{aligned}$$

Thus, ${\hat{\gamma }}_j \vert \vert {\hat{w}}^{j+1} - w^j \vert \vert \rightarrow _{K'} 0$. Using the optimality of ${\hat{w}}^{j+1}$ and $w^{j+1}$ for ($Q (j,i_j-1)$) and $(Q (j,i_j))$, respectively, we find

$$\begin{aligned} \gamma _j \vert \vert w^{j+1} - w^j \vert \vert = \tau {\hat{\gamma }}_j \vert \vert w^{j+1} - w^j \vert \vert \le \tau {\hat{\gamma }}_j \vert \vert {\hat{w}}^{j+1} - w^j \vert \vert \rightarrow _{K'} 0. \end{aligned}$$

Now, one can use a standard subsequence-subsequence argument to conclude that $\gamma _j \vert \vert w^{j+1} - w^j \vert \vert \rightarrow _K 0$ holds along the entire subsequence K.

It remains to verify M-stationarity of ${\bar{w}}$. Since $w^{j+1}$ solves the subproblem (A.4), the corresponding optimality condition yields

$$\begin{aligned} 0 \in \nabla \varphi (w^j) + \gamma _j \big ( w^{j+1} - w^j \big ) + {\mathcal {N}}_D^lim (w^{j+1}). \end{aligned}$$

Due to Proposition 3.2, we also have $w^{j+1} \rightarrow _K {\bar{w}}$. Hence, taking the limit $j \rightarrow _K \infty$ and exploiting once again the upper semicontinuity of the limiting normal cone, we obtain

$$\begin{aligned} 0 \in \nabla \varphi ({\bar{w}}) + {\mathcal {N}}_D^lim ({\bar{w}}), \end{aligned}$$

i.e., ${\bar{w}}$ is an M-stationary point of (3.1). $\square$

Constraint regularity of the MAXCUT problem

Here, we show that all feasible points of (6.3) with

$$\begin{aligned} D:=\left\{ W\in {\mathbb {R}}^{n\times n}_sym \,|\,W \succeq 0, \ {\text {rank}}W \le 1 \right\} \end{aligned}$$

satisfy GMFCQ. Note that we use $G:{\mathbb {R}}^{n\times n}_sym \rightarrow {\mathbb {R}}^n$ given by $G(W):={\text {diag}}W$, $W\in {\mathbb {R}}^{n\times n}_sym$, and $C:=\{e\}$ here in order to model the feasible set of (6.3) in the form given in (P).

Let us fix a feasible matrix $W\in {\mathbb {R}}^{n\times n}_sym$ of (6.3). Then we find a vector $u\in \{\pm n^{-1/2}\}^n$ such that $W=nuu^\top$, i.e., W possesses the non-zero eigenvalue n and the associated eigenvector u.

First, we will show that

$$\begin{aligned} {\mathcal {N}}_D^lim (W) \subset \left\{ Y\in {\mathbb {R}}^{n\times n}_sym \,\big |\,Yu=0\right\} . \end{aligned}$$

(B.1)

For $Y\in {\mathcal {N}}_D^lim (W)$, we find sequences $\{W^k\},\{Y^k\}\subset {\mathbb {R}}^{n\times n}_sym$ and $\{\alpha _k\}\subset [0,\infty )$ such that $W^k\rightarrow W$, $Y^k\rightarrow Y$, and $Y^k\in \alpha _k(W^k-\varPi _D(W^k))$ for all $k\in {\mathbb {N}}$. For each $k\in {\mathbb {N}}$, let $W^k = \sum _{i=1}^n\mu _i^ku_i^k(u_i^k)^\top$ be an (orthonormal) eigenvalue decomposition with non-increasingly ordered eigenvalues $\mu _1^k\ge \mu _2^k\ge \ldots \ge \mu _n^k$ and associated pairwise orthonormal eigenvectors $u_1^k,\ldots ,u_n^k$. Due to $W^k\rightarrow W$, we find $\mu _1^k\rightarrow n$, $\mu _2^k,\ldots ,\mu _n^k\rightarrow 0$, and (along a subsequence without relabeling) $u_1^k\rightarrow \pm u$. For sufficiently large $k\in {\mathbb {N}}$, this implies $\varPi _D(W^k) = \{\mu _1^ku_1^k(u_1^k)^\top \}$, see [51, Proposition 3.4] and Proposition 5.7. Hence, for any such $k\in {\mathbb {N}}$, we find $Y^k=\alpha _k\sum _{i=2}^n\mu _i^ku_i^k(u_i^k)^\top$. Particularly, this gives $Y^ku_1^k=0$ for large enough $k\in {\mathbb {N}}$, so that $Yu=0$ follows by taking the limit $k\rightarrow \infty$.

Second, suppose that there are a vector $\lambda \in {\mathcal {N}}_C(G(W))={\mathbb {R}}^n$ and a matrix $Y\in {\mathcal {N}}_D^lim (W)$ such that ${\text {diag}}\lambda +Y=0$. In order to prove validity of GMFCQ, $\lambda =0$ has to be shown. From (B.1), we find $\lambda \bullet u=-Yu=0$ where $\bullet$ represents the entrywise product operation. Observing that the components of u are all different from zero, $\lambda =0$ follows.