Abstract
We construct an automaton group with a PSPACE-complete word problem, proving a conjecture due to Steinberg. Additionally, the constructed group has a provably more difficult, namely EXPSPACE-complete, compressed word problem and acts over a binary alphabet. Thus, it is optimal in terms of the alphabet size. Our construction directly simulates the computation of a Turing machine in an automaton group and, therefore, seems to be quite versatile. It combines two ideas: the first one is a construction used by D’Angeli, Rodaro and the first author to obtain an inverse automaton semigroup with a PSPACE-complete word problem and the second one is to utilize a construction used by Barrington to simulate Boolean circuits of bounded degree and logarithmic depth in the group of even permutations over five elements.
Similar content being viewed by others
1 Introduction
The word problem is one of Dehn’s fundamental algorithmic problems in group theory [13]: given a word over a finite set of generators for a group, decide whether the word represents the identity in the group. While, in general, the word problem is undecidable [10, 26], many classes of groups have a decidable word problem. Among them is the class of automaton groups. In this context, the term automaton refers to finite state, letter-to-letter transducers. In such automata, every state q induces a length-preserving, prefix-compatible action on the set of words, where an input word u is mapped to the output word obtained by reading u starting in q. The group or semigroup generated by the automaton is the closure under composition of the actions of the different states and a (semi)group arising in this way is called an automaton (semi)group.
The interest in automaton groups was stirred by the observation that many groups with interesting properties are automaton groups. Most prominently, the class contains the famous Grigorchuk group [17] (which is the first example of a group with sub-exponential but super-polynomial growth and admits other peculiar properties, see [18] for an accessible introduction). There is also a quite extensive study of algorithmic problems in automaton (semi)groups: the conjugacy problem and the isomorphism problem (here the automaton is part of the input) – the other two of Dehn’s fundamental problems – are undecidable for automaton groups [31]. Moreover, for automaton semigroups, the order problem could be proved to be undecidable [15, Corollary 3.14]. Recently, this could be extended to automaton groups [16] (see also [5]). On the other hand, the undecidability result for the finiteness problem for automaton semigroups [15, Theorem 3.13] could not be lifted to automaton groups so far.
The undecidability results show that the presentation of groups using automata is still quite powerful. Nevertheless, it is not very difficult to see that the word problem for automaton groups is decidable. One possible way is to show an upper bound on the length of an input word on which a state sequenceFootnote 1 not representing the identity of the group acts non-trivially. In the most general setting, this bound is |Q|n where Q is the state set of the automaton and n is the length of the state sequence. Another viewpoint is that one can use a non-deterministic guess and check algorithm to solve the word problem. This algorithm uses linear space proving that the word problem for automaton (semi)groups is in PSPACE. This approach seems to be mentioned first by Steinberg [30, Section 3] (see also [12, Proposition 2 and 3]). In some special cases, better algorithms or upper bounds are known: for example, for contracting automaton groups (and this includes the Grigorchuk group), the witness length is bounded logarithmically [25] and the problem, thus, is in LOGSPACE; other examples of classes with better upper bounds or algorithms include automata with polynomial activity [8] or Hanoi Tower groups [9]. On the other hand, Steinberg conjectured that there is an automaton group with a PSPACE-complete word problem [30, Question 5]. As a partial solution to his problem, an inverse automaton semigroup with a PSPACE-complete word problem has been constructed in [12, Proposition 6]Footnote 2. In this paper, our aim is to finally prove the conjecture for groups.
First, however, we give a simpler proof for the weaker statement that the uniform word problem for automaton groups (where the group, represented by its generating automaton, is part of the input) is PSPACE-complete in Section 3. This simpler proof uses the same ideas as the main proof and should facilitate understanding the latter.
For the main result, Theorem 10, we adopt the construction used by D’Angeli, Rodaro and the first author from [12, Proposition 6]. This construction uses a master reduction and directly encodes a Turing machine into an automaton. Already in [12, Proposition 6], it was also used to show that there is an automaton group whose word problem with a rational constraint (which depends on the input) is PSPACE-complete. To get rid of this rational constraint, we apply an idea used by Barrington [3] to transform NC1-circuits (circuits of bounded fan-in and logarithmic depth) into bounded-width polynomial-size branching programs. Similar ideas predating Barrington have been attributed to Gurevich (see [22]) and given by Mal’cev [23] but also by Mauerer and Rhodes [24] as well as Krohn, Maurer and Rhodes [20]. Nevertheless, this paper is fully self-contained and no previous knowledge of either [12] or [3] is needed. Barrington’s construction uses the group A5 of even permutations over five elements. However, there is a wide variety of other groups that can be used in a similar way. For example the Grigorchuk group (see [4]) or the free group in three generators (see [28]). Both examples have the advantage that they are – in contrast to A5 – generated by an automaton over a binary alphabet (see [1, 32] for the free group). We will describe our construction in a general way (independent of the group). Afterwards, we can plug in, for example, the mentioned free group in three generators and obtain an automaton group over a binary alphabet with a PSPACE-complete word problem.
Finally, in Section 5, we also investigate the compressed word problem for automaton groups. Here, the (input) state sequence is given as a so-called straight-line program (a context-free grammar which generates exactly one word). Alternatively, the compressed word problem can also be considered as a circuit value problem where the input gates of the circuit are labeled by group elements and the inner gates compute the product of group elements. See [21] or [6, Chapter 4] for more information on the compressed word problem. By uncompressing the input sequence and applying the above mentioned non-deterministic linear-space algorithm, one can see that the compressed word problem can be solved in EXPSPACE. Thus, the more interesting part is to prove that this algorithm cannot be improved significantly: we show that there is an automaton group with an EXPSPACE-hard compressed word problem. This result is interesting because, by taking the disjoint union of the two automata, we obtain a group whose (ordinary) word problem is PSPACE-complete and whose compressed word problem is EXPSPACE-complete and, thus, provably more difficult by the space hierarchy theorem [29, Theorem 6] (or e. g. [27, Theorem 7.2, p. 145] or [2, Theorem 4.8]). To the best of our knowledge, this was the first known example of such a group. Meanwhile, however, Bartholdi, Figelius, Lohrey and the second author found other examples of groups whose compressed word problem is provably harder than their (ordinary) word problem [4]. These examples include the Grigorchuk group, Thompson’s groups and several others defined in terms of wreath products.
Other explicit previous results on the compressed word problem for automaton groups do not seem to exist. However, it was observed by Gillibert [14] that the proof of [12, Proposition 6] also yields an automaton semigroup with an EXPSPACE-complete compressed word problem in a rather straightforward manner. For the case of groups, it is possible to adapt the construction used by Gillibert to prove the existence of an automaton group with an undecidable order problem [16] slightly to obtain an automaton group with a PSPACE-hard compressed word problem [14].
This work is an extended version of the conference paper [34]. The most notable extensions are the simpler proof for the uniform word problem (which was omitted from the conference paper for space reasons) and the extension of the construction to use a binary alphabet instead of one with five elements (which is novel). Parts of the presentation are taken from the first author’s doctoral thesis [33].
2 Preliminaries
Words and Alphabets with Involution
In this paper, we use A ⊎ B for the disjoint union of the sets A and B. Additionally, we use common notations from formal language theory. In particular, we use Σ∗ to denote the set of words over an alphabet Σ including the empty word ε. If we want to exclude the empty word, we write Σ+. For any alphabet Q, we define a natural involution between Q and a disjoint copy Q− 1 = {q− 1∣q ∈ Q} of Q: it maps q ∈ Q to q− 1 ∈ Q− 1 and vice versa. In particular, we have (q− 1)− 1 = q. The involution extends naturally to words over Q± 1 = Q ∪ Q− 1: for \(q_{1}, \dots , q_{n} \in Q^{\pm 1}\), we set \((q_{n} {\dots } q_{1})^{-1} = q_{1}^{-1} {\dots } q_{n}^{-1}\). This way, the involution is equivalent to taking the group inverse if Q is a generating set of a group. To simplify the notation, we write Q±∗ for (Q± 1)∗.
A word u is a prefix of a word v if there is some word x with v = ux. It is a proper prefix if x is non-empty. The set of proper prefixes of some word w is PPre w and PPre L for some language L is \(\text {PPre}\ L = \bigcup _{w \in L} \text {PPre}\ w\).
Turing Machines and Complexity
We assume the reader to be familiar with basic notions of complexity theory (see [27] or [2] for standard text books on complexity theory) such as configurations for Turing machines, computations and reductions in logarithmic space (LOGSPACE) as well as complete and hard problems for PSPACE and the class EXPSPACE. For the class of problems (or functions) solvable (or computable) in deterministic linear space, we write DLINSPACE. We only consider deterministic, single-tape machines and write their configurations as words \(c_{0} {\dots } c_{i - 1}\) \(p c_{i} {\dots } c_{n - 1}\) where the cj are symbols from the tape alphabet and p is a state. In this configuration, the machine is in state p and its head is over the symbol ci. By convention, we assume that the tape symbols at positions − 1 and n are blank symbols.
Using suitable normalizations, we can assume that every Turing machine admits a simple function which describes its transitions:
Fact 1 (Folklore)
Consider a deterministic Turing machine with state set P and tape alphabet Δ. After a straightforward transformation of the transition function and states, we can assume that the symbol \(\gamma _{i}^{(t + 1)}\) at position i of the configuration at time step t + 1 only depends on the symbols \(\gamma _{i - 1}^{(t)}, \gamma _{i}^{(t)}, \gamma _{i + 1}^{(t)} \in {\varGamma }\) at position i − 1, i and i + 1 at time step t. Thus, we may always assume that there is a function τ : (P ⊎Δ)3 → P ⊎Δ mapping the symbols \(\gamma _{i - 1}^{(t)}, \gamma _{i}^{(t)}, \gamma _{i + 1}^{(t)} \in P \uplus {\varDelta }\) to the uniquely determined symbol \(\gamma _{i}^{(t + 1)}\) for all i and t.
Proof Proof Idea
The only problem appears if the machine moves to the left: if we have the situation  or
or  (where the positions i − 1, i and i + 1 are in black) and the machine moves to the left in state p when reading a c but does not move when reading a d, then the new value for the second symbol does not only depend on the symbols right next to it; we can either be in the situation
(where the positions i − 1, i and i + 1 are in black) and the machine moves to the left in state p when reading a c but does not move when reading a d, then the new value for the second symbol does not only depend on the symbols right next to it; we can either be in the situation  or
or  (where position i is in black). To circumvent the problem, we can introduce intermediate states. Now, instead of moving to the left, we go into an intermediate state (without movement). In the next step, we move to the left (but this time the movement only depends on the state and not on the current symbol). □
(where position i is in black). To circumvent the problem, we can introduce intermediate states. Now, instead of moving to the left, we go into an intermediate state (without movement). In the next step, we move to the left (but this time the movement only depends on the state and not on the current symbol). □
Automata
We use the word automaton to denote what is more precisely called a letter-to-letter, finite state transducer. Formally, an automaton is a triple \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\) consisting of a finite set of states Q, an input and output alphabet Σ and a set \(\delta \subseteq Q \times {{\varSigma }} \times {{\varSigma }} \times Q\) of transitions. For a transition (p, a, b, q) ∈ Q ×Σ×Σ× Q, we usually use the more graphical notation  and, additionally, the common way of depicting automata
and, additionally, the common way of depicting automata

where a is the input and b is the output. We will usually work with deterministic and complete automata, i. e. automata where we have

for all p ∈ Q and a ∈Σ. In other words, for every a ∈Σ, every state has exactly one transition with input a.
A run of an automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\) is a sequence

of transitions from δ. It starts in q0 and ends in qn. Its input is \(a_{1} {\dots } a_{n}\) and its output is \(b_{1} {\dots } b_{n}\). If \(\mathcal {T}\) is complete and deterministic, then, for every state q ∈ Q and every word u ∈Σ∗, there is exactly one run starting in q with input u. We write q ∘ u for its output and q ⋅ u for the state in which it ends. This notation can be extended to multiple states. To avoid confusion, we usually use the term state sequence instead of “word” (which we reserve for input or output words) for elements q ∈ Q∗. Now, for states \(q_{1}, q_{2}, \dots , q_{\ell } \in Q\), we set \(q_{\ell } {\dots } q_{2} q_{1} \circ u = q_{\ell } {\dots } q_{2} \circ (q_{1} \circ u)\) inductively. If the state sequence q ∈ Q∗ is empty, then q ∘ u is simply u.
This way, every state q ∈ Q (and even every state sequence q ∈ Q∗) induces a map Σ∗→Σ∗ and every word u ∈Σ∗ induces a map Q → Q. If all states of an automaton induce bijective functions, we say it is invertible and call it a \({\mathscr{G}}\)-automaton. In this case, we let the function induced by the inverse q− 1 of a state q be the inverse of the function induced by q. For a \({\mathscr{G}}\)-automaton \(\mathcal {T}\), all bijections induced by the states generate a group (with composition as operation), which we denote by \({\mathscr{G}}(\mathcal {T})\). A group is called an automaton group if it arises in this way. Clearly, \({\mathscr{G}}(\mathcal {T})\) is generated by the maps induced by the states of \(\mathcal {T}\) and, thus, finitely generated.
Example 2
The typical first example of an automaton generating a group is the adding machine \(\mathcal {T} = (\{ q, \text {id} \}, \{ 0, 1 \}, \delta )\):

It obviously is deterministic and complete and, therefore, we can consider the map induced by the state q. We have q3 ∘ 000 = q2 ∘ 100 = q ∘ 010 = 110. From this example, it is easy to see that the action of q is to increment the input word (which is interpreted as a reverse/least significant bit first binary representation \(\overleftarrow {\text {bin}}(n)\) of a number n). The inverse is accordingly to decrement the value. As the other state id acts like the identity, we obtain that the group \({\mathscr{G}}(\mathcal {T})\) generated by \(\mathcal {T}\) is isomorphic to the infinite cyclic group.
Similar to extending the notation q ∘ u to state sequences, we can also extend the notation q ⋅ u. For this, it is useful to introduce cross diagrams, another notation for transitions of automata. For a transition  of an automaton, we write the cross diagram given in Fig. 1a. Multiple cross diagrams can be combined into a larger one. For example, the cross diagram in Fig. 1b indicates that there is a transition
of an automaton, we write the cross diagram given in Fig. 1a. Multiple cross diagrams can be combined into a larger one. For example, the cross diagram in Fig. 1b indicates that there is a transition  for all 1 ≤ i ≤ n and 1 ≤ j ≤ m. Typically, we omit unneeded names for states and abbreviate cross diagrams. Such an abbreviated cross diagram is depicted in Fig. 1c. If we set \(\boldsymbol {p} = q_{n, 0} {\dots } q_{1, 0}\), \(u = a_{0, 1} {\dots } a_{0, m}\), \(v = a_{n, 1} {\dots } a_{n, m}\) and \(\boldsymbol {q} = q_{n, m} {\dots } q_{1, m}\), then it indicates the same transitions as in Fig. 1b. It is important to note here that the right-most state in p is actually the one to act first.
for all 1 ≤ i ≤ n and 1 ≤ j ≤ m. Typically, we omit unneeded names for states and abbreviate cross diagrams. Such an abbreviated cross diagram is depicted in Fig. 1c. If we set \(\boldsymbol {p} = q_{n, 0} {\dots } q_{1, 0}\), \(u = a_{0, 1} {\dots } a_{0, m}\), \(v = a_{n, 1} {\dots } a_{n, m}\) and \(\boldsymbol {q} = q_{n, m} {\dots } q_{1, m}\), then it indicates the same transitions as in Fig. 1b. It is important to note here that the right-most state in p is actually the one to act first.
If we have the cross diagram from Fig. 1c, we set p ⋅ u = q. This is the same, as setting \(q_n {\ldots } q_1 \cdot u = [q_n {\dots } q_2 \cdot (q_1 \circ u)] (q_1 \cdot u)\) inductively and, with the definition from above, we already have p ∘ u = v.
Group Theory and Word Problem
For the neutral element of a group, we write  . We write p =Gq or p = q in G if two words p and q over the generators (and their inverses) of a group evaluate to the same group element. Typically, G will be an automaton group generated by a \({\mathscr{G}}\)-automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\) and p and q are state sequences from Q±∗.
. We write p =Gq or p = q in G if two words p and q over the generators (and their inverses) of a group evaluate to the same group element. Typically, G will be an automaton group generated by a \({\mathscr{G}}\)-automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\) and p and q are state sequences from Q±∗.
The word problem of a group G generated by a finite set Q is the decision problem:
Constant: the group G generated by Q Input: q ∈ Q±∗ Question: is
in G?
In addition, if \(\mathcal {C}\) is a class of groups, we also consider the uniform word problem for \(\mathcal {C}\). Here, the group \(G \in \mathcal {C}\) is part of the input (in a suitable representation).
Balanced Iterated Commutators
For elements h and g of a group G, we write gh for the conjugation h− 1gh of g with h and [h, g] for the commutator h− 1g− 1hg. Both notations extend naturally to words over the group generators: if G is generated by Q, then we let pq = q− 1pq and [q, p] = q− 1p− 1qp for p, q ∈ Q±∗.
Commutators can be used to simulate logical conjunctions in groups since we have  if
if  or
or  . To create a D-ary logical conjunction, we can nest multiple binary conjunctions in a tree of logarithmic depth and we can use the same idea with commutators.Footnote 3
. To create a D-ary logical conjunction, we can nest multiple binary conjunctions in a tree of logarithmic depth and we can use the same idea with commutators.Footnote 3
Definition 3
Let Q be an alphabet and  For \(\boldsymbol {p}_{0}, \dots , \boldsymbol {p}_{\kern -0.25ex {2D - 1}} \in Q^{\pm *}\) with D = 2d, we define the word \(B_{\beta , \alpha }[\boldsymbol {p}_{\kern -0.25ex {D - 1}}, \dots , \boldsymbol {p}_{0}]\) inductively on d by
For \(\boldsymbol {p}_{0}, \dots , \boldsymbol {p}_{\kern -0.25ex {2D - 1}} \in Q^{\pm *}\) with D = 2d, we define the word \(B_{\beta , \alpha }[\boldsymbol {p}_{\kern -0.25ex {D - 1}}, \dots , \boldsymbol {p}_{0}]\) inductively on d by
We also write Bβ, α for α ∈ Q±∗ or β ∈ Q±∗, where we identify α and β with the constant maps n↦α and n↦β, respectively.
One part of using \(B_{\beta , \alpha }[\boldsymbol {p}_{\kern -0.25ex {D - 1}}, \dots , \boldsymbol {p}_{0}]\) as a logical conjunction is that it collapses to the neutral element if one of the pi is equal to the neutral element.
Fact 4
Let G be a group generated by some (finite) set Q, \(\alpha , \beta : \mathbb {N} \to Q^{\pm *}\) and \(\boldsymbol {p}_{0}, \dots , \boldsymbol {p}_{\kern -0.25ex {D - 1}} \in Q^{\pm *}\) for some D = 2d. If there is some i with  in G, we have
in G, we have  in G.
in G.
Proof
We show the fact by induction on d. For d = 0 (or, equivalently, D = 1), there is nothing to show. So, consider the step from d to d + 1 (or, equivalently, from D to 2D). If we have 0 ≤ i < D, then, by induction, we have

The case D ≤ i < 2D is symmetric. □
The other part of using \(B_{\beta , \alpha }[\boldsymbol {p}_{\kern -0.25ex {D - 1}}, \dots , \boldsymbol {p}_{0}]\) as a logical conjunction – namely that \(B_{\beta , \alpha }[\boldsymbol {p}_{\kern -0.25ex {D - 1}}, \dots , \boldsymbol {p}_{0}]\) is nontrivial for proper choices of the pi – depends on the actual underlying group.
Example 5
A simple way to use Bβ, α as a logical conjunction is the group A5 of even permutations over five elements. It was used by Barrington [3] to convert logical circuits of bounded fan-in and logarithmic depth (so-called NC1-circuits) to bounded-width, polynomial-size branching programs.
Since A5 is finite, we can use the entire group as a finite generating set. We let σ = (13254), α = (23)(45) and β = (245). A straightforward calculation shows that we have
for this choice (compare to [3, Lemma 1 and 3]), which allows us to use Bβ, α as a D-ary logical conjunction. In fact, it is even quite simple because α and β are constant (and do not depend on the level d).
The idea is that we consider  as false and σ as true. Now, to use Bβ, α as a logical conjunction, we show
as false and σ as true. Now, to use Bβ, α as a logical conjunction, we show

for all \(g_{0}, \dots , g_{\kern -0.25ex {D - 1}} \in \{ \text {id}, \sigma \} \subseteq A_5\) where D = 2d. We show the case \(g_{0} = {\dots } = g_{\kern -0.25ex {D - 1}} = \sigma \) by induction on d and the case  for some i follows by Fact 4. For d = 0 (or, equivalently, D = 1), there is nothing to show. So, consider the step from d to d + 1 (or, equivalently, from D to 2D), where we have
for some i follows by Fact 4. For d = 0 (or, equivalently, D = 1), there is nothing to show. So, consider the step from d to d + 1 (or, equivalently, from D to 2D), where we have
by induction and the choice of σ, α and β.
Normal commutators and conjugation are compatible in the sense that we have [h, g]k = [hk,gk] for all elements g, h, k of a group. The commutators from Definition 3 satisfy a similar compatibility that we will exploit below.
Fact 6
Let G be a group generated by some (finite) set Q, \(\alpha , \beta : \mathbb {N} \to Q^{\pm *}\) and γ ∈ Q±∗ such that γ commutes with α(d) and β(d) in G for all d. Then, we have for all \(\boldsymbol {p}_{0}, \dots , \boldsymbol {p}_{\kern -0.25ex {D - 1}} \in Q^{\pm *}\) and with D = 2d
Proof
We prove the statement by induction on d. For d = 0 (or, equivalently, D = 1), we have \(B_{\beta , \alpha }[\boldsymbol {p}_{0}]^{\gamma } = \boldsymbol {p}_{0}^{\gamma } = B_{\beta , \alpha }[\boldsymbol {p}_{0}^{\gamma }]\) and, for the step from d to d + 1 (or, equivalently, from D to 2D), we have in G:
□
For our later reductions, it will be important to compute \(B_{\beta , \alpha }[\boldsymbol {p}_{\kern -0.25ex {D - 1}}, \dots , \boldsymbol {p}_{0}]\) in logarithmic space, which is possible due to the logarithmic nesting depth.
Lemma 7
If the functions α and β are computable in DLINSPACE (where the input is given in binary), we can compute \(B_{\beta , \alpha }[\boldsymbol {p}_{\kern -0.25ex {D - 1}}, \dots , \boldsymbol {p}_{0}]\) on input of \(\boldsymbol {p}_{0}, \dots , \boldsymbol {p}_{\kern -0.25ex {D - 1}}\) in logarithmic space.
Proof
We give a sketch for a (deterministic) algorithm which computes the symbol at position i of \(B_{\beta , \alpha }[\boldsymbol {p}_{\kern -0.25ex {D - 1}}, \dots , \boldsymbol {p}_{0}]\) (as a word where we consider α(d), β(d), the pi and their inverses as letters) in logarithmic space. Later, we can expand this by filling in the actual state sequences over Q±∗ (which can be computed in space logarithmic in D). For D = 2d (with d > 0), we have
and the length ℓ(D) of \(B_{\beta , \alpha }[\boldsymbol {p}_{\kern -0.25ex {D - 1}}, \dots , \boldsymbol {p}_{0}]\) (again as a word where we consider α(d), β(d), the pi and their inverses as letters) is given by ℓ(1) = 1 and \(\ell (D) = 8 + 4 \ell (\frac {D}{2})\). This yields
and, thus, that the length of \(B_{\beta , \alpha }[\boldsymbol {p}_{\kern -0.25ex {D - 1}}, \dots , \boldsymbol {p}_{0}]\) is polynomial in D. Therefore, we can iterate the algorithm for all positions 1 ≤ i ≤ ℓ(D) to output \(B_{\beta , \alpha }[\boldsymbol {p}_{\kern -0.25ex {D - 1}}, \dots , \boldsymbol {p}_{0}]\) entirely.
To compute the symbol at position i, we first check whether i is the first or last position (notice that we need the exact value of ℓ(D) for testing the latter). In this case, we know that it is β(d − 1)− 1 or α(d − 1), respectively. Similarly, we can do this for the positions in the middle and at one or three quarters. If the position falls into one of the four recursion blocks, we use two pointers into the input: left and right. Depending on the block, left and right either point to p0 and \(\boldsymbol {p\!}_{\frac {D}{2} - 1}\) or to \(\boldsymbol {p\!}_{\frac {D}{2}}\) and \(\boldsymbol {p}_{\kern -0.25ex {D - 1}}\). Additionally, we also store whether we are in an inverse block or a non-inverse block and keep track of d as a binary number. We need to decrease d by one in every recursion step. Note that \(d = \log D\) as a binary number has length \(\log \log D\) (up to constants) and can, thus, certainly be stored in logarithmic space.Footnote 4 From now on, we disregard the input left of left and right of right (and do appropriate arithmetic on i) and can proceed recursively. If we need to perform another recursive step, we update the variables left and right (instead of using new ones). Therefore, the whole recursion can be done in logarithmic space. □
Normally, we cannot simply apply Bβ, α to a cross diagram as the output interferes and we could get into different states. However, it is possible if the rows of the cross diagram act like the identity (as we then can clearly re-order rows without interference):
Fact 8
Let \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\) be some \({\mathscr{G}}\)-automaton, u ∈Σ∗, \(\alpha , \beta : \mathbb {N} \to Q^{\pm *}\) and \(\boldsymbol {p}_{0}, \dots , \boldsymbol {p}_{\kern -0.25ex {D - 1}} \in Q^{\pm *}\) be state sequences with D = 2d such that we have the cross diagrams

for all d where \(\alpha ^{\prime }(d), \beta ^{\prime }(d), \boldsymbol {q}_{0}, \dots , \boldsymbol {q}_{\kern -0.25ex {D - 1}} \in Q^{\pm *}\). Then, we also have

3 Uniform Word Problem
We start by showing that the uniform word problem for automaton groups is PSPACE-complete. Although this also follows from the non-uniform case proved below, it uses the same ideas but allows for a simpler construction. This way, it serves as a good starting point and makes understanding the more complicated construction below easier.
The general idea is to reduce the PSPACE-complete [19, Lemma 3.2.3]Footnote 5DFA Intersection ProblemFootnote 6
Constant: \({\varGamma } = \{ a_1, \dots , a_4 \}\)
Input: \(D \in \mathbb {N}\) and deterministic finite acceptors
\(\mathcal {A}_{0} = (P_{0}, {\varGamma }, \tau _{0}, p_{0, 0}, F_{0}), \dots ,\)
\(\mathcal {A}_{\kern -0.25ex {D - 1}} = (P_{\kern -0.25ex {D - 1}}, {\varGamma }, \tau _{\kern -0.25ex {D - 1}}, p_{0, D - 1}, F_{\kern -0.25ex {D - 1}})\)
Question: is \(\bigcap _{i = 0}^{D - 1} L(\mathcal {A}_i) = \emptyset \)?
in logarithmic space to the uniform word problem for automaton groups. The output automaton basically consists of the input acceptors and obviously stores in the states the information whether an input word was accepted or not. Finally, we use a logical conjunction based on the commutator Bβ, α to extract whether there is an input word that gets accepted by all acceptors. While we could use other groups for the logical conjunction, we will stick for now to the group A5 from Example 5 for the sake of simplicity.
Theorem 9
The uniform word problem for automaton groups
Constant: \({{\varSigma }} = \{ a_1, \dots , a_5 \}\)
Input: a \({\mathscr{G}}\)-automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\), p ∈ Q±∗
Question: is
in \({\mathscr{G}}(\mathcal {T})\)?
(even over a fixed alphabet with five elements) is PSPACE-complete.
Proof
It is known that the uniform word problem for automaton groupsFootnote 7 is in PSPACE (using a guess and check algorithm; see [30] or [12, Proposition 2]). Thus, we only have to show that the problem is PSPACE-hard. As already mentioned, we reduce the DFA Intersection Problem
Constant: \({\varGamma } = \{ a_1, \dots , a_4 \}\)
Input: \(D \in \mathbb {N}\) and deterministic finite acceptors
\(\mathcal {A}_{0} = (P_{0}, {\varGamma }, \tau _{0}, p_{0, 0}, F_{0}), \dots ,\)
\(\mathcal {A}_{\kern -0.25ex {D - 1}} = (P_{\kern -0.25ex {D - 1}}, {\varGamma }, \tau _{\kern -0.25ex {D - 1}}, p_{0, D - 1}, F_{\kern -0.25ex {D - 1}})\)
Question: is \(\bigcap _{i = 0}^{D - 1} L(\mathcal {A}_i) = \emptyset \)?
to the uniform word problem for automaton groups in logarithmic space. As mentioned above, Kozen [19, Lemma 3.2.3] showed that this problem is PSPACE-hard.
For the reduction, we need to map the acceptors \(\mathcal {A}_{0} = (P_{0}, {\varGamma }, \tau _{0}, p_{0, 0}, F_{0}), \dots , \mathcal {A}_{\kern -0.25ex {D - 1}} = (P_{\kern -0.25ex {D - 1}}, {\varGamma }, \tau _{\kern -0.25ex {D - 1}}, p_{0, D - 1}, F_{\kern -0.25ex {D - 1}})\) to an automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\) and a state sequence p ∈ Q±∗. Without loss of generality, we can assume D = 2d here for some d (otherwise, we can just duplicate one of the input acceptors until we reach a power of two, which can be done in logarithmic space).
We assume the state sets Pi to be pairwise disjoint and set \(P = \{ \text {id}, \sigma \} \uplus \bigcup _{i = 0}^{D - 1} P_i\) and \(F = \bigcup _{i = 0}^{D - 1} F_i\). Additionally, we set \({{\varSigma }} = \{ a_1, \dots , a_4 \} \uplus \{ \$ \}\) and assume that the elements σ, α, β ∈ A5 (from Example 5) act as the corresponding permutations on Σ. For the transitions, we set

Thus, we take the union of the acceptors and extend it into an automaton by letting all states act like the identity. With the new letter $ (the “end-of-word” symbol), we go to id for non-accepting states and to σ for accepting ones. Finally, we have the state id, which acts like the identity, and the state σ, whose action is to apply the permutation σ to all letters of the input word, justifying the re-use of the name σ. Finally, we define \(\mathcal {T}\) as the (disjoint) union of the just defined automaton (P, Σ, δ) with the automaton

Notice that \(\mathcal {T}\) is deterministic, complete and invertible and that all states except σ, α and β act like the identity on words not containing $. Also note that on input of \(\mathcal {A}_{0}, \dots , \mathcal {A}_{\kern -0.25ex {D - 1}}\), the automaton can clearly be computed in logarithmic space.
For the state sequence, we set \(\boldsymbol {p} = B_{0}[p_{0, D - 1}, \dots , p_{0, 0}]\) where we use B0 as a short-hand notation for the balanced commutator \(B_{\beta _{0}, \alpha _{0}}\) defined in Definition 3. Observe that, by Lemma 7, we can compute p in logarithmic space (α0 and β0 are even constant functions in our setting).
This completes our description of the reduction and it remains to show its correctness. If there is some \(w \in \bigcap _{i = 1}^{\ell } L(\mathcal {A}_i)\), we have to show  . We have
. We have

where all qf, i ∈ Fi are final states. Thus, by Fact 8, we also have

where we used B as an abbreviation for Bβ, α. Without loss of generality, we may assume σ(a1)≠a1 and, since we have \(B[\sigma , \dots , \sigma ] = \sigma \) in A5 and also in \({\mathscr{G}}(\mathcal {T})\) (see Example 5), we obtain p ∘ w$a1 = w$σ(a1)≠w$a1.
If, on the other hand, \(\bigcap _{i = 0}^{D - 1} L(\mathcal {A}_i) = \emptyset \), we have to show  . For this, let w ∈Σ∗ be arbitrary. If w does not contain any $, we do not need to show anything since, by construction, only the states σ, α and β act non-trivially on these words and they can only be reached after reading a $. If w contains $, we can write w = u$v with \(u \in \{ a_1, \dots , a_4 \}^{*}\). Since the intersection is empty, there is some \(i \in \{ 0, \dots , D - 1 \}\) with \(u \not \in L(\mathcal {A}_i)\) and we obtain
. For this, let w ∈Σ∗ be arbitrary. If w does not contain any $, we do not need to show anything since, by construction, only the states σ, α and β act non-trivially on these words and they can only be reached after reading a $. If w contains $, we can write w = u$v with \(u \in \{ a_1, \dots , a_4 \}^{*}\). Since the intersection is empty, there is some \(i \in \{ 0, \dots , D - 1 \}\) with \(u \not \in L(\mathcal {A}_i)\) and we obtain

where \(g_{0}, \dots , g_{\kern -0.25ex {D - 1}} \in \{ \text {id}, \sigma \}\). Again, we also obtain the cross diagram

by Fact 8 but, this time, we have  in A5 since gi = id (see Fact 4). Accordingly, we have p ∘ u$v = u$v. □
in A5 since gi = id (see Fact 4). Accordingly, we have p ∘ u$v = u$v. □
4 Non-Uniform Word Problem
In this section, we are going to lift the result from the previous section to the non-uniform case. We show:
Theorem 10
There is an automaton group with a PSPACE-complete word problem:
Constant: a \({\mathscr{G}}\)-automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\) with |Σ| = 2
Input: q ∈ Q±∗
Question: is
in \({\mathscr{G}}(\mathcal {T})\)?
In order to prove this theorem, we are going to adapt the construction used in [12, Proposition 6] to show that there is an inverse automaton semigroup with a PSPACE-complete word problem and that there is an automaton group whose word problem with a single rational constraint is PSPACE-complete. The main idea is to do a reduction directly from a Turing machine accepting an arbitrary PSPACE-complete problem.
Let M be such a deterministic, polynomially space-bounded Turing machine with input alphabet Λ, tape alphabet Δ, blank symbol  , state set P, initial state p0 and accepting states \(F \subseteq P\). Thus, for any input word of length n, all configurations of M are of the form
, state set P, initial state p0 and accepting states \(F \subseteq P\). Thus, for any input word of length n, all configurations of M are of the form  with ℓ + 1 + m = s(n) for some polynomial s. This makes the word problem of M
with ℓ + 1 + m = s(n) for some polynomial s. This makes the word problem of M
Constant: the PSPACE machine M
Input: w ∈Λ∗ of length n
Question: does M reach a configuration with a state from F from the initial configuration
PSPACE-complete and we will eventually do a co-reduction to the word problem of a \({\mathscr{G}}\)-automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\). In fact, we will not work with the Turing machine M directly but instead use the transition function τ : Γ3 →Γ for Γ = P ⊎Δ from Fact 1.
Our automaton \(\mathcal {T}\) operates in two modes. In the first mode, which we will call the “TM mode”, it interprets its input word as a sequence of configurations of M and verifies that the configuration sequence constitutes a valid computation. This verification is done by multiple states (where each state is responsible for a different verification part) and the information whether the verification was successful is stored in the state, not by manipulating the input word. So we have successful states and fail states. Upon reading a special input symbol, the automaton will switch into a second mode, the “commutator mode”. More precisely, successful states go into a dedicated “okay” state r and the fail states go into a state which we call id for reasons that become apparent later. Finally, to extract the information from the states, we use the iterated commutator from Definition 3.
Eventually, we want the alphabet of the automaton to only contain two letters. However, we will first describe how the TM mode of the automaton works for more letters (using an automaton \(\mathcal {T}^{\prime }\)) and then how we can encode this automaton over two letters. Finally, we will extend this encoding with the commutator mode part of the automaton to eventually obtain \(\mathcal {T}\).
Generalized Check-Marking
The idea for the TM mode is similar to Kozen’s approach for showing that the DFA Intersection Problem is PSPACE-complete [19, Lemma 3.2.3]: the input word is interpreted as a sequence of configurations of a PSPACE Turing machine where each configuration is of length s(n):
In Kozen’s proof, there is an acceptor for each position i of the configurations with 0 ≤ i < s(n) which checks for all t whether the transition from \(\gamma _i^{(t)}\) to \(\gamma _i^{(t + 1)}\) is valid. In our case, however, the automaton must not depend on the input (or its length n) and we have to handle this a bit differently. The first idea is to use a “check-mark approach”. First, we check all first positions (\(\gamma _{0}^{(0)}, \gamma _{0}^{(1)}, \dots \)) for valid transitions. Then, we put a check-mark on all these first positions, which tells us that we now have to check all second positions (\(\gamma _1^{(0)}, \gamma _1^{(1)}, \dots \), i. e. the first ones without a check-mark). Again, we put a check-mark on all these, continue with checking all third positions and so on (Fig. 2).
The problem with this approach is that the check-marking leads to an intrinsically non-invertible automaton (see Fig. 3).
To circumvent this, we generalize the check-mark approach: in front of each symbol \(\gamma _{i}^{(t)}\) of a configuration, we add a 0k block (of sufficient length k). In the spirit of Example 2, we interpret this block as representing a binary number. We consider the symbol following the block as “unchecked” if the number is zero; for all other numbers, it is considered as ‘checked”. Now, checking the next symbol boils down to incrementing each block until we have encountered a block whose value was previously zero (and this can be detected while doing the increment). This idea is depicted in Fig. 4. It would also be possible to have the check-mark block after each symbol instead of before (which might be more intuitive) but it turns out that our ordering has some technical advantages.
Construction of \(\mathcal {T}^{\prime }\)
Using the check-mark approach, we can construct the automaton \(\mathcal {T}^{\prime }\), which implements the TM mode over the alphabet \({{\varSigma }}^{\prime } = \{ 0, 1, \#, \$ \} \cup {\varGamma }\). Our automaton will have two dedicated states r and id. The semantics of them is that r is an “okay” state while id is a “fail” state. Both states will only be entered after reading the first $ and, for now, we let them both operate as the identity but later, when we describe the commutator mode of the automaton, we will replace r with a non-identity state.Footnote 8
The idea is that the input of the automaton is of the form u$v where u is in ({0,1,#}∪Γ)∗ and describes a computation of M (with digit blocks for the generalized check-marking approach). We will define multiple state sequences where each one checks a different aspect of whether the computation is valid and accepting for some given input word w ∈Λ∗ for the Turing machine. If such a check passes, we basically end in the state r after reading the $ and, if it fails, we end in a state sequence only containing ids. This way, all checking state sequences end in r if and only if M accepts w. This information will later be extracted in the commutator mode described below.
Proposition 11
There is a \({\mathscr{G}}\)-automaton \(\mathcal {T}^{\prime } = (Q^{\prime }, {{\varSigma }}^{\prime }, \delta ^{\prime })\) with an identity state id, a dedicated state \(r \in Q^{\prime }\) and alphabet \({{\varSigma }}^{\prime } = {{\varSigma }}_{1} \cup \{ \$ \}\) for Σ1 = {0,1,#}∪Γ such that, on input of w ∈Λ∗, one can compute state sequences pi for 0 ≤ i < D (for some D ≥ 1) in logarithmic space so that the following holds:
For every \(u \in {{\varSigma }}_{1}^{*}\) and all 0 ≤ i < D, we have pi ∘ u$ = u$ and
-
1.
if M accepts w, then there is some \(u \in {{\varSigma }}_{1}^{*}\) such that, for all 0 ≤ i < D, we have \(\boldsymbol {p}_{i} \cdot u \$ \in \text {id}^{*} r \text {id}^{*}\) and
-
2.
if M does not accept w, then, for all \(u \in {{\varSigma }}_{1}^{*}\), there is some 0 ≤ i < D such that we have \(\boldsymbol {p}_{i} \cdot u \$ \in \text {id}^{*}\).
Proof
The automaton \(\mathcal {T}^{\prime }\) is the union of several simpler automata. We will use 0 and 1 for the generalized check-mark approach, # is used to separate individual configurations and $ acts as an “end-of-computation” symbol switching the automaton to one of the special states r or id. We call the first part of an input word form \({{\varSigma }}_{1}^{*}\) the TM part (because we consider it to encode a computation of M) and everything after the first $ the commutator part (because we will only use it later).
The first part of the automaton contains the two special states r and id, which we both let act as the identityFootnote 9 but it helps to think of id as a “fail” state and r as an “okay” state (like the final states in the proof of Theorem 9):

Here, we have introduced a convention: we use arrows labeled by idA for some \(A \subseteq {{\varSigma }}^{\prime }\) to indicate that we have an a/a-transition for all a ∈ A.
Next, we add a part to our automaton to check that the TM part of the input is of the formFootnote 10\((0^{*} {\varGamma })^{+} \left (\# (0^{*} {\varGamma })^{+} \right )^{*}\):

where we have introduced another convention: whenever a transition is missing for some \(a \in {{\varSigma }}^{\prime }\), there is an implicit a/a-transition to the state id (as defined above). Additionally, dotted states refer to the corresponding states defined above.
Note that we do not check that the factors in (0∗Γ)+ correspond to well-formed configurations for the Turing machine here. This will be done implicitly by checking that the input word belongs to a valid computation of the Turing machine, which we describe below.
We also need a part which checks whether the TM part of the input word contains a final state (if this is not the case, we want to “reject” the word):

Finally, we come to the more complicated parts of \(\mathcal {T}^{\prime }\). The first one is for the generalized check-marking as described above and is depicted in Fig. 5, which we actually need twice: once for g = r and once for g = id. Notice, however, that, during the TM mode (i. e. before the first $), both versions of \(\checkmark _{\!\!\!g}\) behave exactly the same way; the only difference is after switching to the commutator mode: while \(\checkmark _{\!\!\!\text {id}}\) always goes to id, \(\checkmark _{\!\!\!r}\) goes to r (if the check-marking was successful and to id, otherwise).
Additionally, we also need an automaton part verifying that every configuration symbol has been check-marked (in the generalized sense):

The last part is for checking the validity of the transitions at all first so-far unchecked positions. While it is not really difficult, this part is a bit technical. Intuitively, for checking the transition from time step t − 1 to time step t at position i, we need to compute \(\gamma _{i}^{(t)} = \tau (\gamma _{i - 1}^{(t - 1)}, \gamma _{i}^{(t - 1)}, \gamma _{i + 1}^{(t - 1)})\) from the configuration symbol at positions i − 1, i and i + 1 for time step t − 1. We store \(\gamma _{i}^{(t)}\) in the state (to compare it to the actual value). Additionally, we need to store the last two symbols of configuration t we have encountered so far (for computing what we expect in the next time step later on) and whether we have seen a 1 or only 0s in the check-mark digit block. For all this, we use the states

with \(\gamma _{-1}, \gamma _{0}, \gamma _{0}^{\prime } \in {\varGamma }\). The idea is the following. In the  and
and  states, we store the value we expect for the first unchecked symbol (γ0) and the last symbol we have seen in the current configuration (γ− 1). We are in the
states, we store the value we expect for the first unchecked symbol (γ0) and the last symbol we have seen in the current configuration (γ− 1). We are in the  state if we have not seen any 1 in the digit block yet and in the
state if we have not seen any 1 in the digit block yet and in the  if we did. The two states on the right are used to skip the rest of the current configuration and to compute the symbol we expect for the first unchecked position in the next configuration (\(\gamma _{0}^{\prime }\)).
if we did. The two states on the right are used to skip the rest of the current configuration and to compute the symbol we expect for the first unchecked position in the next configuration (\(\gamma _{0}^{\prime }\)).
We use these states in the transitions schematically depicted in Fig. 6. Here, the dashed transitions exist for all \(\gamma _{-1}^{\prime }\) and γ1 in Γ but go to different states, respectively, and the dotted states correspond to the respective non-dotted states with different values for γ0 and γ− 1 (with the exception of r, which corresponds to the state defined above). We also define \(q_{\gamma ^{\prime }}\) as the state on the bottom right (for \(\gamma ^{\prime } \in {\varGamma }\)).
The automaton parts depicted in Figs. 5 and 6 are best understood with an example. Consider the input word
where we consider the \(\gamma _i^{(t)}\) to form a valid computation. If we start in state \(q_{\gamma _1^{(0)}}\) and read the above word, we immediately take the 1/1-transition and go into the corresponding  state where we skip the rest of the digit block. Using the dashed transition, the next symbol \(\gamma _{0}^{(0)}\) takes us back into a
state where we skip the rest of the digit block. Using the dashed transition, the next symbol \(\gamma _{0}^{(0)}\) takes us back into a  -state where the upper entry is still \(\gamma _1^{(0)}\) but the lower entry is now \(\gamma _{0}^{(0)}\) (i. e. the last configuration symbol we just read). We loop at this state while reading the next three 0s and, since the next symbol \(\gamma _1^{(0)}\) matches with the one stored in the state, we get into the state with entries \(\gamma _{0}^{(0)}, \gamma _1^{(0)}\) where we skip the next three 0s again. Reading \(\gamma _2^{(0)}\) now gets us into the state with entry \(\gamma _1^{(1)}\) since we have \(\tau (\gamma _{0}^{(0)}, \gamma _1^{(0)}, \gamma _2^{(0)}) = \gamma _1^{(1)}\) by assumption that the \(\gamma _i^{(t)}\) form a valid computation. Here, we read #/# and the process repeats for the second configuration, this time starting in \(q_{\smash {\gamma _1^{(1)}}}\). When reading the final $, we are in the state with entry \(\tau (\gamma _{0}^{(1)}, \gamma _1^{(1)}, \gamma _2^{(1)})\) and finally go to r. Notice that during the whole process, we have not changed the input word at all!
-state where the upper entry is still \(\gamma _1^{(0)}\) but the lower entry is now \(\gamma _{0}^{(0)}\) (i. e. the last configuration symbol we just read). We loop at this state while reading the next three 0s and, since the next symbol \(\gamma _1^{(0)}\) matches with the one stored in the state, we get into the state with entries \(\gamma _{0}^{(0)}, \gamma _1^{(0)}\) where we skip the next three 0s again. Reading \(\gamma _2^{(0)}\) now gets us into the state with entry \(\gamma _1^{(1)}\) since we have \(\tau (\gamma _{0}^{(0)}, \gamma _1^{(0)}, \gamma _2^{(0)}) = \gamma _1^{(1)}\) by assumption that the \(\gamma _i^{(t)}\) form a valid computation. Here, we read #/# and the process repeats for the second configuration, this time starting in \(q_{\smash {\gamma _1^{(1)}}}\). When reading the final $, we are in the state with entry \(\tau (\gamma _{0}^{(1)}, \gamma _1^{(1)}, \gamma _2^{(1)})\) and finally go to r. Notice that during the whole process, we have not changed the input word at all!
If we now start reading the input word again in state \(\checkmark _{\!\!\!r}\) (see Fig. 5 and also refer to Fig. 4), we turn the first 1 into a 0, go to the state at the bottom, turn the next 0 into a 1 and go to the state on the right, where we ignore the next 0. When reading \(\gamma _{0}^{(0)}\), we go back to \(\checkmark _{\!\!\!r}\). Next, we take the upper exit and turn the next 0 into a 1. The remaining 0s are ignored and we remain in the state at the top right until we read \(\gamma _1^{(0)}\) and go to the state at the top left. Here, we ignore everything up to #, which gets us back into \(\checkmark _{\!\!\!r}\). The second part works in the same way with the difference that we go to r at the end since we encounter the $ instead of #. The output word, thus, is
and we have check-marked the next position in both configurations.
This concludes the definition of the automaton and the reader may verify that \(\mathcal {T}^{\prime }\) is indeed a \({\mathscr{G}}\)-automaton since all individual parts are \({\mathscr{G}}\)-automata. Furthermore, apart from the check-marking, no state has a non-identity transitions. Also note that $ is not modified by any state. □
Definition of the State Sequences
It remains to define the state sequences pi that satisfy the conditions from the proposition. First, all state sequences pi need to act trivially on words from \({{\varSigma }}_1^{*}\) and, after reading the first $, we will either be in a state sequence from id∗r id∗ (this is the “successful” case) or from id∗ (this is the “fail” case). Second, we need to satisfy the two implications. The idea is that we have some \(u \in {{\varSigma }}_1^{*}\) which describes a computation of the Turing machine M on input w. Each pi verifies a certain aspect of the computation. If the Turing machine accepts (first implication), there is some u encoding the valid and accepting computation and all verifications will pass (i. e. we end up in state sequences from id∗r id∗). If the Turing machine does not accept the input w (second implication), then no \(u \in {{\varSigma }}_1^{*}\) can describe a valid and accepting computation and at least one verification will fail for all such u (i. e. we end up in a state sequence from id∗).
We simply use the state p0 = z to verify that u is from \((0^{*} {\varGamma })^+ \left (\# (0^{*} {\varGamma })^+ \right )^{*}\). Thus, we only need to consider the case that u is of the form
with \(\gamma _i^{(t)} \in {\varGamma }\) any further. Also observe that p0 acts trivially on all words from \({{\varSigma }}_1^{*} \) by construction.
To test that u encodes a valid and accepting computation, we need to verify that, for every 0 ≤ i < s(n), we can check-mark the first i positions. For this, we let
as we have the cross diagram

where \(\overleftarrow {\text {bin}}(z)\) denotes the reverse/least significant bit first binary representation of z (of sufficient length). In particular, ci acts trivially on all words \(u \in {{\varSigma }}_1^{*}\) since \(\checkmark _{\!\!\!r}\) acts in the same way as \(\checkmark _{\!\!\!\text {id}}\) on such words (i. e. any change made is reverted later). Here, it is useful to observe that, if the 0 block for \(\gamma _j^{(t)}\) with j ≤ i is not long enough to count to its required value (including the case that it is empty), then we will always end up in id after reading a $. The same happens if Lt < i + 1 (i. e. if one of the configurations is “too short”). So this guarantees, Lt ≥ s(n) for all t.
On the other hand, we use
to ensure that, after check-marking the first s(n) positions in every configurations, all symbols have been check-marked (i. e. that no configuration is “too long”), which guarantees Lt = s(n) for all t. Again, \(\boldsymbol {c}^{\prime }\) does not change words from \({{\varSigma }}_1^{*}\).
Now that we have ensured that the word is of the correct form and we can count high enough for our check-marking, we need to actually verify that the \(\gamma _i^{(t)}\) constitute a valid computation of the Turing machine with the initial configuration  for the input word w. To do this, we define
for the input word w. To do this, we define
for every 0 ≤ i < s(n) as we have the cross diagram

if \(\gamma _i^{(t)}\) is the expected \(\gamma _i^{\prime }\). Otherwise (if \(\gamma _i^{(t)} \neq \gamma _i^{\prime }\)), we always end in the state id after reading the first $. Finally, to ensure that the computation is not only valid but also accepting, we use the state p2 + 2s(n) = f. Both, qi and f do not change words from \({{\varSigma }}_1^{*}\).
Finally, we observe that we can compute all pi with 0 ≤ i < D = 3 + 2s(n) in logarithmic space on input w ∈Λ∗.
The Two Implications
For the first implication, we assume that the Turing machine M accepts on the initial configuration  . Let
. Let
be the corresponding computation with \(\gamma _{0}^{(0)} = p_{0}\), \(\gamma _1^{(0)} {\dots } \gamma _{n}^{(0)} = w\) and \(\gamma _i^{(T)} \in F\) for some 0 ≤ i < s(n). We choose \(\ell = \lceil \log (s(n)) \rceil + 1\) and define
The reader may verify that we have the cross diagram depicted in Fig. 7 for this choice of u (we only have to combine the cross diagrams given above for the individual pi). This shows the first implication.
For the second implication, assume that no valid computation of M on the initial configuration  contains an accepting state from F and consider an arbitrary word \(u \in {{\varSigma }}_1^{*}\). If u is not of the form \((0^{*} {\varGamma })^+ \left (\# (0^{*} {\varGamma })^+ \right )^{*}\) , we have the cross diagram
contains an accepting state from F and consider an arbitrary word \(u \in {{\varSigma }}_1^{*}\). If u is not of the form \((0^{*} {\varGamma })^+ \left (\# (0^{*} {\varGamma })^+ \right )^{*}\) , we have the cross diagram

and, thus, satisfied the implication (with i = 0).
Therefore, we assume u to be of the form mentioned in (†) and use a similar argumentation for the remaining cases. If u does not contain a state from F, then we end up in the state id after reading $ for f. As w is not accepted by the machine, this includes in particular all valid computations on the initial configuration  . If one of the 0 blocks in u is too short to count to a value required for the check-marking (i. e. one \(\ell _i^{(t)}\) is too small), then the corresponding ci will go to a state sequence from id∗. This is also true if one configuration is too short (i. e. Lt < s(n) for some t). If one configuration is too long (i. e. Lt > s(n)), then this will be detected by \(\boldsymbol {c}^{\prime }\) as not all positions will be check-marked after check-marking all first s(n) positions in every configuration. Finally, qi yields a state sequence from id∗ if \(\gamma _i^{(0)}\) is not the correct symbol from the initial configuration or if we have \(\gamma _i^{(t + 1)} \neq \tau (\gamma _{i - 1}^{(t)}, \gamma _i^{(t)}, \gamma _{i + 1}^{(t)})\) for some t (where we let
. If one of the 0 blocks in u is too short to count to a value required for the check-marking (i. e. one \(\ell _i^{(t)}\) is too small), then the corresponding ci will go to a state sequence from id∗. This is also true if one configuration is too short (i. e. Lt < s(n) for some t). If one configuration is too long (i. e. Lt > s(n)), then this will be detected by \(\boldsymbol {c}^{\prime }\) as not all positions will be check-marked after check-marking all first s(n) positions in every configuration. Finally, qi yields a state sequence from id∗ if \(\gamma _i^{(0)}\) is not the correct symbol from the initial configuration or if we have \(\gamma _i^{(t + 1)} \neq \tau (\gamma _{i - 1}^{(t)}, \gamma _i^{(t)}, \gamma _{i + 1}^{(t)})\) for some t (where we let  ).
).
Remark 12
The constructed automaton \(\mathcal {T}^{\prime }\) has 3|Γ|2 + |Γ| + 19 states (including the special states r and id and the additional 5 states belonging to \(\checkmark _{\!\!\!\text {id}}\) in Fig. 5) where |Γ| is the sum of the number of states and the number of tape symbols for a Turing machine for a PSPACE-complete problem.
Encoding over Two Letters
Eventually, the automaton \(\mathcal {T}\) should operate over a binary alphabet Σ. We will achieve this by using an automaton group with a binary alphabet where we still can implement a D-ary logical conjunction using nested commutators. However, for now, we will keep things a bit more general and also consider larger alphabets. This will allow us to generally describe our approach for various groups.Footnote 11
Assume that Σ contains at least two distinct symbols  and
and  . We will use these two symbols to encode the computations of the Turing machine M. We let \(\tilde {{{\varSigma }}} =\)
. We will use these two symbols to encode the computations of the Turing machine M. We let \(\tilde {{{\varSigma }}} =\) and, without loss of generality, assume that |Γ| = 2L is a power of two and \({\varGamma } = \{ \gamma _{0}, \dots , \gamma _{|{\varGamma }| - 1} \}\). We interpret the symbols {0,1,#, $}∪Γ in the alphabet of \(\mathcal {T}^{\prime }\) (from Proposition 11) as the words
and, without loss of generality, assume that |Γ| = 2L is a power of two and \({\varGamma } = \{ \gamma _{0}, \dots , \gamma _{|{\varGamma }| - 1} \}\). We interpret the symbols {0,1,#, $}∪Γ in the alphabet of \(\mathcal {T}^{\prime }\) (from Proposition 11) as the words

over  where
where  is the binary representation of i with length L,
is the binary representation of i with length L,  as the zero digit and
as the zero digit and  as the one digit. Furthermore, we let
as the one digit. Furthermore, we let  and
and  .
.
Remark 13
Note that every word in  can be uniquely decomposed into a product of words from X, which means that X is a code (in the definition of [7]). Since no word in X is a prefix of another one, we obtain that X is even a prefix code.
can be uniquely decomposed into a product of words from X, which means that X is a code (in the definition of [7]). Since no word in X is a prefix of another one, we obtain that X is even a prefix code.
Not every word in Σ∗ is in X∗; not even every word in  . However, we have that every word in
. However, we have that every word in  is a prefix of a word in X∗. This can be proven by using the following fact.
is a prefix of a word in X∗. This can be proven by using the following fact.
Fact 14
For our special choice of 0,1,#, and Γ, we have

If a word is not a prefix of Y∗$Σ∗, it must contain a symbol from \(\tilde {{{\varSigma }}}\):
Lemma 15
If u ∈Σ∗ is not a prefix of a word in Y∗$Σ∗, then u is in \(Y^{*} (\text {PPre}\ Y) \tilde {{{\varSigma }}} {{\varSigma }}^{*}\) (where  ).
).
Proof
We factorize u = u1u2au3 with u1 maximal in Y∗, u2 maximal in PPre Y (both possibly empty), a ∈Σ and u3 ∈Σ∗. We show  by contradiction. So, assume a
by contradiction. So, assume a  . We have
. We have  (PPreX) ∪ X (where the last inclusion follows by Fact 14). Since we have PPre$ =
(PPreX) ∪ X (where the last inclusion follows by Fact 14). Since we have PPre$ =  , we obtain PPre X = PPre Y and, combining this with the last statement, u2a ∈ (PPre Y ) ∪ X. We cannot have u2a ∈PPre Y since u2 was chosen maximal with this property. Similarly, we cannot have u2a ∈ Y since u1 was chosen maximal. The only remaining case u2a = $ is not possible either, however, since, then, u was in Y∗$Σ∗, which violates the hypothesis. □
, we obtain PPre X = PPre Y and, combining this with the last statement, u2a ∈ (PPre Y ) ∪ X. We cannot have u2a ∈PPre Y since u2 was chosen maximal with this property. Similarly, we cannot have u2a ∈ Y since u1 was chosen maximal. The only remaining case u2a = $ is not possible either, however, since, then, u was in Y∗$Σ∗, which violates the hypothesis. □
We can now describe how we can encode the automaton \(\mathcal {T}^{\prime }\) from Proposition 11 over Σ. For this, it is important that all transitions of \(\mathcal {T}^{\prime }\) are of a special form. Namely, the symbols #, and γi ∈Γ are not changed by any transition and 0 and 1 are either also not changed or they are toggled (i. e. we either have the transitions  and
and  or the transitions
or the transitions  and
and  ).
).
The general idea to obtain the encoded automaton \(\mathcal {T}_2 = (Q_2, {{\varSigma }}, \delta _2)\) from \(\mathcal {T}^{\prime } = (Q^{\prime }, \{ 0, 1, \#, \$ \} \cup {\varGamma }, \delta ^{\prime })\) is not to read 0,1,#, and the elements of Γ as single symbols but to use a tree to read the prefixes of their encodings as words over  . When we know which encoding we have read, we move to the corresponding state (and reset the prefix of the current encoding); additionally, we possibly also toggle 0 and 1 if the corresponding state in the original automaton did this. Here comes the special encoding we have chosen above into play: we could not simply toggle γ0 and \(\gamma _{2^{L} - 1}\), for example, because it is not clear how to do this in a prefix-compatible way.
. When we know which encoding we have read, we move to the corresponding state (and reset the prefix of the current encoding); additionally, we possibly also toggle 0 and 1 if the corresponding state in the original automaton did this. Here comes the special encoding we have chosen above into play: we could not simply toggle γ0 and \(\gamma _{2^{L} - 1}\), for example, because it is not clear how to do this in a prefix-compatible way.
To formalize this general idea, we consider the set 
 and let \(P^{\prime } = Q^{\prime } \setminus \{ r, \text {id} \}\) and
and let \(P^{\prime } = Q^{\prime } \setminus \{ r, \text {id} \}\) and

where we use the convention (r, ε) = r and (id,ε) = id. The first line in the definition of \(\delta ^{\prime \prime }\) extends r and id into identities over Σ. The second and third line handle the case  . The fourth and fifth line are for the case
. The fourth and fifth line are for the case  and the last two lines are for
and the last two lines are for  . By Fact 14, this covers all cases and we have an outgoing transition with input
. By Fact 14, this covers all cases and we have an outgoing transition with input  and one with input
and one with input  for every q ∈ Q2 (since \(\mathcal {T}^{\prime }\) must be a complete automaton over {0,1,#, $}∪Γ). Therefore, to make \(\mathcal {T}_2\) complete, we only have to handle the letters in
for every q ∈ Q2 (since \(\mathcal {T}^{\prime }\) must be a complete automaton over {0,1,#, $}∪Γ). Therefore, to make \(\mathcal {T}_2\) complete, we only have to handle the letters in  and, to this end, we let
and, to this end, we let

Observe that this turns \(\mathcal {T}_2\) into a \({\mathscr{G}}\)-automaton over Σ.
Example 16
Using the just described encoding method, a schematic part

of the automaton \(\mathcal {T}^{\prime }\) yields the part

of the automaton \(\mathcal {T}_2\) (where the possibly missing transitions all go to id).
Remark 17
An important point to note on this encoding is that we have all cross diagrams from \(\mathcal {T}^{\prime }\) also in \(\mathcal {T}_2\) (if we identify \(p^{\prime } \in P^{\prime }\) with \((p^{\prime }, \varepsilon )\)). In particular, we still have the statements from Proposition 11 about the words \(u \in {{\varSigma }}_1^{*}\) also for \(\mathcal {T}_2\) and the words from Y∗.
Additionally, the encoding ensures that we always end in id after reading a word from \(Y^{*} (\text {PPre}\ Y) \tilde {{{\varSigma }}}\). Since no pi from Proposition 11 changes a word from \(u \in {{\varSigma }}_1^{*}\) in \(\mathcal {T}^{\prime }\), this shows the following fact.
Fact 18
We have

in \(\mathcal {T}_2\) for all u ∈ Y∗PPreY, \(a \in \tilde {{{\varSigma }}}\) and 0 ≤ i < D.
Remark 19
The encoded automaton \(\mathcal {T}_2\) has \((|\mathcal {T}^{\prime }| - 2)(|{\varGamma }| + 3) + 2\) many states where |Γ| is the sum of the number of states and the number of tape symbols for a Turing machine for a PSPACE-complete problem (which we assume to be a power of two) and \(|\mathcal {T}^{\prime }|\) is the size of \(\mathcal {T}^{\prime }\) from Remark 12. This yields 3|Γ|3 + 10|Γ|2 + 20|Γ| + 53 many states in total, where 2 states are id and r and 5 ⋅ (|Γ| + 3) = 5|Γ| + 15 additional states belong to (the encoding of) \(\checkmark _{\!\!\!\text {id}}\).
The Commutator Mode
For the commutator mode, we fix an arbitrary \({\mathscr{G}}\)-automaton \(\mathcal {R} = (R, {{\varSigma }}, \rho )\) which admits DLINSPACE-computable functions \(\alpha , \beta : \mathbb {N} \to R^{\pm *}\) (where the input is given in binary) and a LOGSPACE-computable function b
Input: a number D in unary with D = 2d for some d
(i. e. the string 1D) and
a number 0 ≤ i < D in binary
Output: b(D, i) ∈ R±∗
with

for all (positive) powers D of two. Note that the choice of \(\mathcal {R}\) implies |Σ|≥ 2.
Similar to A5 in Example 5, we use this group to simulate a logical conjunction. For state sequences \(\boldsymbol {p}_{0}, \dots , \boldsymbol {p}_{\kern -0.25ex {D - 1}} \in R^{\pm *}\) with  or pi = b(D, i) in \({\mathscr{G}}(\mathcal {R})\) for all 0 ≤ i < D, we have
or pi = b(D, i) in \({\mathscr{G}}(\mathcal {R})\) for all 0 ≤ i < D, we have  in \({\mathscr{G}}(\mathcal {R})\) if and only if we have
in \({\mathscr{G}}(\mathcal {R})\) if and only if we have  in \({\mathscr{G}}(\mathcal {R})\) for all 0 ≤ i < D.
in \({\mathscr{G}}(\mathcal {R})\) for all 0 ≤ i < D.
Example 20
One possible choice for \(\mathcal {R}\) is to continue using the group A5 from Example 5 where we have shown  for the special elements α, β, σ ∈ A5. The group A5 is an automaton group as it is generated, e. g., by the \({\mathscr{G}}\)-automaton with states A5, alphabet \(\{ 1, 2, \dots , 5 \}\) and transitions
for the special elements α, β, σ ∈ A5. The group A5 is an automaton group as it is generated, e. g., by the \({\mathscr{G}}\)-automaton with states A5, alphabet \(\{ 1, 2, \dots , 5 \}\) and transitions

and we can simply let b(D, i) = σ for all 0 ≤ i < D, which obviously make b LOGSPACE-computable. Of course, the two constant functions α and β are DLINSPACE-computable. Thus, we can choose A5 for \({\mathscr{G}}(\mathcal {R})\).
Example 21
Another possibility for \(\mathcal {R}\) is the first Aleshin automaton

which generates the free group F3 in the generators a, b and c with a binary alphabet [1, 32].Footnote 12
We claim that we have  in F3 if we choose
in F3 if we choose
and b(D, i) = b− 1a for all 0 ≤ i < D. To show the claim, we write B3(D) for
where D = 2d and show
and that B3(2d) is freely reduced in both cases by induction (on d). From this, we obtain that all B3(2d) are freely reduced but non-empty and, therefore, not the identity in F3.
For d = 0 (or, equivalently, D = 1), we have
which is in b− 1{a, b, c}±∗a and freely reduced. For the inductive step from d to d + 1 (or, equivalently, from D to 2D), we have:
We distinguish two cases. If d is even (and, equivalently, d + 1 is odd), we have β(d) = c (by definition) and B3(2d) = b− 1wa freely reduced for some w (by induction). Thus, we obtain
which is freely reduced and in c− 1{a, b, c}±∗a (as desired since d + 1 is odd). The other case is that d is odd (and d + 1 is even). Here, we have β(d) = b and B3(2d) = c− 1wa freely reduced for some w. This yields
which is again freely reduced and in b− 1{a, b, c}±∗a (as desired since d + 1 is even).
On a side note, we point out that this argument only requires that all b(D, i) are from b− 1{a, b, c}±∗a, not that they are all equal or even all equal to b− 1a (as we have chosen them here). This will become more important later on in Section 5 because it allows us to also use b(D, i) which are nested commutators of the from Bβ, ε themselves.
Remark 22
Instead of using Bβ, α for DLINSPACE-computable functions α and β, we could restrict ourselves to Bε, ε. The idea here is that we can move the conjugation to the leaves of the tree representing the nested commutators.
A schematic representation of such a tree can be found in Fig. 8 for D = 23, where the labels at the edges indicate a conjugation. From the picture, it becomes apparent that the conjugating element for b(D, i) with D = 2d is coupled to the reverse/least significant bit first binary representation of i with length d.
Formally, we can define \(w(D, i) = f(\overleftarrow {\text {bin}}_{d}(i))\) for D = 2d for the function f that works as follows: the first letter of \(\overleftarrow {\text {bin}}_{d}(i)\) is replaced with α(0) if it is a zero digit or with β(0) if it is a one digit, the second letter is replaced with α(1) (if it is a zero digit) or with β(1) (if it is a one digit), and so on. The counter for the positions in \(\overleftarrow {\text {bin}}_{d} (i)\), which is the argument to α and β, needs to count up to d and, thus, requires space \(\log \log D\). Therefore, w(D, i) can certainly be computed in LOGSPACE (in particular, if D is given in unary).
For the group A5 (from Example 20), we can replace all zero digits by α and all one digits by β and, for F3 (from Example 21), the function f is implemented by the automatonFootnote 13

Now, we define \(b^{\prime }(D, i) = b(D, i)^{w(D, i)}\) (which clearly is still LOGSPACE-computable) and show
for all D = 2d. In fact, we have
for all \(\boldsymbol {p}_{0}, \dots , \boldsymbol {p}_{\kern -0.25ex {D - 1}} \in R^{\pm *}\), which we show by induction on d. For d = 0 (or, equivalently, D = 1), we have \(B_{\varepsilon , \varepsilon } [ \boldsymbol {p}_{0}^{w(1, 0)} ] = \boldsymbol {p}_{0}^{\varepsilon } = \boldsymbol {p}_{0} = B_{\beta , \alpha } [ \boldsymbol {p}_{0} ]\). For the inductive step from d to d + 1 (or, equivalently, form D to 2D), we observe
for all 0 ≤ i < D and
for all D ≤ i < 2D. Thus, we have in \({\mathscr{G}}(\mathcal {R})\):
Example 23
In fact, we can choose any automaton group that satisfies the uniformly SENS property of [4] for \({\mathscr{G}}(\mathcal {R})\). These include, for example, the Grigorchuk group generated by the automaton

The definition of a uniformly SENS group is very similar but slightly stronger than what we require for our group \({\mathscr{G}}(\mathcal {R})\) for the commutator mode:
A group G generated by a finite set R is called uniformly strongly efficiently non-solvable(uniformly SENS)Footnote 14 if there is a constant \(\mu \in \mathbb {N}\) and words rd, v ∈ R±∗ for all \(d \in \mathbb {N}\), v ∈{0,1}≤d such that
-
(a)
|rd, v|≤ 2μd for all v ∈{0,1}d,
-
(b)
\(\boldsymbol {r}_{d,v} = \bigl [ \boldsymbol {r}_{d, 1v}, \boldsymbol {r}_{d, 0v} \bigr ]\) for all v ∈{0,1}<d (here we take the commutator of words)Footnote 15,
-
(c)
 in G and
in G and -
(d)
given v ∈{0,1}d, a positive integer i encoded in binary with μd bits, and a ∈ R± one can decide in DLINTIME whether the ith letter of rd, v is a. Here, DLINTIME is the class of problems decidable in linear time on a random access Turing machine.
Essentially, a group is uniformly SENS if there are non-trivial balanced iterated commutators of arbitrary depth and these balanced iterated commutators can be computed efficiently.
To define the elements b(D, i) for a uniformly SENS automaton group, we let \(b(D, i) = \boldsymbol {r}_{d, \overleftarrow {\text {bin}}_{d}(i)}\) where D = 2d and \(\overleftarrow {\text {bin}}_{d}(i)\) is the reverse/least significant bit first binary representation of i with length d. For this choice, we have  in the group (and, thus, choose α = β = ε, which is clearly DLINSPACE-computable).
in the group (and, thus, choose α = β = ε, which is clearly DLINSPACE-computable).
It remains to show that b is LOGSPACE-computable (where D is given in unary). Observe that the last condition (d) requires that each letter of rd, v can be computed in time μd on a random access Turing machine. Thus, it can, in particular, be computed in space μd on a normal (non-random access) Turing machine. Since, by the first condition (a), its length is at most 2μd, we only need a counter of size μd to compute rd, v entirely. Thus, we can compute b(D, i) in space \(\mu \log D\), which is logarithmic in the input as D is given in unary (i. e. as a string 1D).
Proof Proof of Theorem 10
Since the uniform word problem for automaton groups is in PSPACE (see Theorem 9), so is the word problem of any (fixed) automaton group. Therefore, we only have to show the hardness part of the result.
As already stated at the beginning of this section, we reduce the PSPACE-complete word problem for M to the (complement of the) word problem for a \({\mathscr{G}}\)-automaton \(\mathcal {T}\) with state set Q. For this reduction, it remains to finally construct \(\mathcal {T}\) and to map an input w ∈Λ∗ for the Turing machine M to a state sequence q ∈ Q±∗ in such a way that q can be computed from w in logarithmic space and that we have  if and only if the Turing machine does not accept w.
if and only if the Turing machine does not accept w.
We first define the \({\mathscr{G}}\)-automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\), which is composed of multiple parts. Its first part is the automaton \(\mathcal {R} = (R, {{\varSigma }}, \rho )\). If we want to show Theorem 10 for |Σ| = 2, we have to choose a suitable \(\mathcal {R}\) over the binary alphabet  (see Examples 21 and 23 for such choices). However, we will continue the proof without this assumption and also allow other groups (such as A5 from Example 20).
(see Examples 21 and 23 for such choices). However, we will continue the proof without this assumption and also allow other groups (such as A5 from Example 20).
Next, we take the automaton \(\mathcal {T}^{\prime }\) from Proposition 11 and encode it into the automaton \(\mathcal {T}_{2}\) over Σ. Then, for every r ∈ R, we take a disjoint copy \(\mathcal {T}_{2, r}\) of \(\mathcal {T}_{2}\). Each copy \(\mathcal {T}_{2, r}\) contains the place-holder state r (mentioned in Proposition 11) and we replace it with the actual state r from \(\mathcal {R}\) which belongs to the respective copy (see Fig. 9). Thus, in general, the action of r is not the identity anymore. By pi, r, we denote the corresponding pi from Proposition 11 for \(\mathcal {T}_{2, r}\).
Finally, we consider the \({\mathscr{G}}\)-automaton \(\mathcal {R}_{0}\)

over the alphabet \({{\varSigma }}^{\prime } = \{ 0, 1, \#, \$ \} \cup {\varGamma }\) (where we use the same convention about edges labeled by idA as in the proof of Proposition 11). We encode \(\mathcal {R}_{0}\) over Σ (similar to the encoding \(\mathcal {T}_{2}\) of \(\mathcal {T}^{\prime }\)) by using the automaton

and, again, take a disjoint copy \(\mathcal {R}_{0, r}\) for every r where we replace the place-holder r by the actual state from \(\mathcal {R}\). These parts of \(\mathcal {T}\) will be used to implement the conjugation with α(d) and β(d) in Bβ, α (just like in the proof of Theorem 9). For this, we define the functions \(\alpha _{0}, \beta _{0}: \mathbb {N} \to Q^{\pm *}\). We let α0(d) (respectively: β0(d)) be the same as α(d) (respectively: β(d)) with the only difference being that we replace every r ∈ R by the corresponding state r0 from the appropriate copy of \(\mathcal {R}_{0, r}\). Clearly, α0 and β0 are DLINSPACE-computable (since α and β are). As an abbreviation, we write B for Bβ, α and B0 for \(B_{\beta _{0}, \alpha _{0}}\) in the rest of this proof.
This completes the definition of \(\mathcal {T}\) and it remains to define the state sequence q depending on w ∈Λ∗. For this, we first compute (in logarithmic space) all state sequences pi, r with 0 ≤ i < D and r ∈ R from Proposition 11 (with respect to the appropriate copy \(\mathcal {T}_{2, r}\)) using w as the input. Here, we may assume that D = 2d is a power of two (otherwise, we repeat pD− 1,r as a new pD, r for all r ∈ R until we reach a power of two, which is possible in logarithmic space). Then, we compute in logarithmic space the elements \(\boldsymbol {b}_{0} = b(D, 0), \dots , \boldsymbol {b}_{\kern -0.25ex {D - 1}} = b(D, D - 1) \in R^{\pm *}\) such that  in \({\mathscr{G}}(\mathcal {R})\) (which is possible by the choice of \(\mathcal {R}\) above). Note that \({\mathscr{G}}(\mathcal {R})\) is a subgroup of \({\mathscr{G}}(\mathcal {T})\) since \(\mathcal {R}\) is a sub-automaton of \(\mathcal {T}\). Thus, we have
in \({\mathscr{G}}(\mathcal {R})\) (which is possible by the choice of \(\mathcal {R}\) above). Note that \({\mathscr{G}}(\mathcal {R})\) is a subgroup of \({\mathscr{G}}(\mathcal {T})\) since \(\mathcal {R}\) is a sub-automaton of \(\mathcal {T}\). Thus, we have  in \({\mathscr{G}}(\mathcal {T})\). Now, for every 0 ≤ i < D, we can compute \(\boldsymbol {b}_{i}^{\prime } = \boldsymbol {p}_{i, r_{\ell }} {\ldots } \boldsymbol {p}_{i, r_{1}}\) in logarithmic space from \(\boldsymbol {b}_{i} = r_{\ell } {\dots } r_{1}\) with \(r_{1}, \dots , r_{\ell } \in R^{\pm 1}\). Finally, we choose \(\boldsymbol {q} = B_{0}[\boldsymbol {b}_{\kern -0.25ex {D - 1}}^{\prime }, \dots , \boldsymbol {b}_{0}^{\prime }]\) (which can also be computed in logarithmic space by Lemma 7).
in \({\mathscr{G}}(\mathcal {T})\). Now, for every 0 ≤ i < D, we can compute \(\boldsymbol {b}_{i}^{\prime } = \boldsymbol {p}_{i, r_{\ell }} {\ldots } \boldsymbol {p}_{i, r_{1}}\) in logarithmic space from \(\boldsymbol {b}_{i} = r_{\ell } {\dots } r_{1}\) with \(r_{1}, \dots , r_{\ell } \in R^{\pm 1}\). Finally, we choose \(\boldsymbol {q} = B_{0}[\boldsymbol {b}_{\kern -0.25ex {D - 1}}^{\prime }, \dots , \boldsymbol {b}_{0}^{\prime }]\) (which can also be computed in logarithmic space by Lemma 7).
We need to show  in \({\mathscr{G}}(\mathcal {T})\) if and only if M does not accept w. First, assume that M accepts w and consider an arbitrary 0 ≤ i < D. We have \(\boldsymbol {b}_{i} = r_{\ell } {\dots } r_{1}\) for some \(r_{1}, \dots , r_{\ell } \in R^{\pm 1}\) and \(\boldsymbol {b}_{i}^{\prime } = \boldsymbol {p}_{i, r_{\ell }} {\ldots } \boldsymbol {p}_{i, r_{1}}\). By Proposition 11 (first implication, applied to the appropriate copies of \(\mathcal {T}^{\prime }\)) and by Remark 17, there is some u ∈ Y∗ such that we have the cross diagramFootnote 16
in \({\mathscr{G}}(\mathcal {T})\) if and only if M does not accept w. First, assume that M accepts w and consider an arbitrary 0 ≤ i < D. We have \(\boldsymbol {b}_{i} = r_{\ell } {\dots } r_{1}\) for some \(r_{1}, \dots , r_{\ell } \in R^{\pm 1}\) and \(\boldsymbol {b}_{i}^{\prime } = \boldsymbol {p}_{i, r_{\ell }} {\ldots } \boldsymbol {p}_{i, r_{1}}\). By Proposition 11 (first implication, applied to the appropriate copies of \(\mathcal {T}^{\prime }\)) and by Remark 17, there is some u ∈ Y∗ such that we have the cross diagramFootnote 16

Combining these cross diagrams (for all 0 ≤ i < D), we obtain the black part of the cross diagram

Since we have r0 ⋅ u$ = r and r0 ∘ u$ = u$ by the construction of \(\mathcal {R}_{0}\), we also have the cross diagrams

for all d and can add the commutators to the above cross diagram by Fact 8 to obtain the gray additions. As we have  in \({\mathscr{G}}(\mathcal {T})\), there must be some v ∈Σ∗ such that
in \({\mathscr{G}}(\mathcal {T})\), there must be some v ∈Σ∗ such that
which concludes this direction.
For the other direction, assume that M does not accept the input w. We have to show \(\boldsymbol {q} \circ u^{\prime } = B_{0}[\boldsymbol {b}_{\kern -0.25ex {D - 1}}^{\prime }, \dots , \boldsymbol {b}_{0}^{\prime }] \circ u^{\prime } = u^{\prime }\) for all \(u^{\prime } \in {{\varSigma }}^{*}\). First, we show this for all \(u^{\prime } \in Y^{*} \$ {{\varSigma }}^{*}\) (and, thus, also for all prefixes of such \(u^{\prime }\)) where we let \(u^{\prime } = u \$ v\) with u ∈ Y∗ and v ∈Σ∗. Our approach is similar to the one given above for the case that M accepts w. Again, consider an arbitrary 0 ≤ i < D with \(\boldsymbol {b}_{i} = r_{\ell } {\dots } r_{1}\) for some \(r_{1}, \dots , r_{\ell } \in R^{\pm 1}\) and, thus, \(\boldsymbol {b}_{i}^{\prime } = \boldsymbol {p}_{i, r_{\ell }} {\ldots } \boldsymbol {p}_{i, r_{1}}\). We have the cross diagram

for this i by Proposition 11. However, this time, there is some, 0 ≤ i < D with \(\boldsymbol {b}_{i}^{\prime } \cdot u \$ \in \text {id}^{*}\) and, thus, equal to  in \(\mathscr {{G}(\mathcal {T})}\) (this follows from applying the second implication of Proposition 11 to all \(r_{1}, \dots , r_{\ell }\)).Footnote 17
in \(\mathscr {{G}(\mathcal {T})}\) (this follows from applying the second implication of Proposition 11 to all \(r_{1}, \dots , r_{\ell }\)).Footnote 17
Again, we can combine these cross diagrams to obtain the black part of

and, then, add the gray part using Fact 8. Since we have  in \({\mathscr{G}}(\mathcal {T})\) for some i, we obtain (for the state sequence on the right)
in \({\mathscr{G}}(\mathcal {T})\) for some i, we obtain (for the state sequence on the right)  in \({\mathscr{G}}(\mathcal {T})\) by Fact 4. Thus, we have \(\boldsymbol {q} \circ u \$ v = B_{0}[\boldsymbol {b}_{\kern -0.25ex {D - 1}}^{\prime }, \dots , \boldsymbol {b}_{0}^{\prime }] \circ u \$ v = u \$ v\).
in \({\mathscr{G}}(\mathcal {T})\) by Fact 4. Thus, we have \(\boldsymbol {q} \circ u \$ v = B_{0}[\boldsymbol {b}_{\kern -0.25ex {D - 1}}^{\prime }, \dots , \boldsymbol {b}_{0}^{\prime }] \circ u \$ v = u \$ v\).
Now, assume that \(u^{\prime }\) is not a prefix of a word in Y∗$Σ∗. Then, it is in \(Y^{*} (\text {PPre}\ Y) \tilde {{{\varSigma }}} {{\varSigma }}^{*}\) by Lemma 15 and we can factorize \(u^{\prime } = u a v\) for some u ∈ Y∗(PPre Y ), \(a \in \tilde {{{\varSigma }}}\) and v ∈Σ∗. By Fact 18, we obtainFootnote 18

for 0 ≤ i < D with \(\boldsymbol {b}_{i} = r_{\ell } {\dots } r_{1}\) (where \(r_{1}, \dots , r_{\ell } \in R^{\pm 1}\)). Using the same argumentation, we also obtain r0 ∘ ua = ua and  in \({\mathscr{G}}(\mathcal {T})\) for all r0 in the copies of \(\mathcal {R}_{0, 2}\) and, thus, for all d, the cross diagrams
in \({\mathscr{G}}(\mathcal {T})\) for all r0 in the copies of \(\mathcal {R}_{0, 2}\) and, thus, for all d, the cross diagrams

We can combine this into the cross diagram

(where we get the gray part by Fact 8) and obtain
□
Remark 24
To calculate the number of states of \(\mathcal {T}\), we assume that all parts of the automaton share the same id state and the same part for \(\checkmark _{\!\!\!\text {id}}\); the r states are shared anyway. This yields
many states, where |R| is the number of states of \(\mathcal {R}\) (for example, |R| = 3 for the Aleshin automaton from Example 21), |Γ| is the sum of the number of states and the number of tape symbols for a Turing machine for a PSPACE-complete problem (which we assume to be a power of two) and where we have used the size of \(\mathcal {T}_{2}\) from Remark 19.
5 Compressed Word Problem
In this section, we re-apply our previous construction to show that there is an automaton group with an EXPSPACE-complete compressed word problem. The compressed word problem of a group is similar to the normal word problem. However, the input element (to be compared to the neutral element) is not given directly but as a straight-line program. A straight-line program is a context-free grammar which generates exactly one word.
Theorem 25
There is an automaton group with an EXPSPACE-complete compressed word problem:
Constant: a \({\mathscr{G}}\)-automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\) with |Σ| = 2
Input: a straight-line program generating a state sequence q ∈ Q±∗
Question: is
in \({\mathscr{G}}(\mathcal {T})\)?
The hard part of the proof of Theorem 25 is (again) that the problem is EXPSPACE-hard. That it is contained in EXPSPACE follows immediately by uncompressing the straight-line program (which yields at most an exponential blow up) and then applying the PSPACE-algorithm for the normal word problem.
The outline of the proof for the EXPSPACE-hardness is the same as for the (normal) word problem: we start with a Turing machine M and construct a \({\mathscr{G}}\)-automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\) from it in the same way as in the proof of Theorem 10. This time, however, the Turing machine accepts an (arbitrary) EXPSPACE-complete problem and we assume that the length of its configurations is \(s(n) = n + 1 + 2^{2n^{e}}\) for some positive integer e where n is the length of the input for M. Additionally, we assume the same normalizations as before.
To keep things a bit simpler here, we do not use an arbitrary \({\mathscr{G}}\)-automaton \(\mathcal {R} = (R, {{\varSigma }}, \rho )\) for the commutators but fix the Aleshin automaton generating the free group F3 (from Example 21) for \(\mathcal {R}\) in this section. In fact, it is even a bit more convenient to use the union of the Aleshin automaton \(\mathcal {A} = (R_{1}, {{\varSigma }}, \eta )\) (where we also include the inverse states a− 1,b− 1 and c− 1) with its second power \(\mathcal {A}^{2}\) for \(\mathcal {R}\). The second power of an automaton is its composition with itself. Formally, \(\mathcal {A}^{2}\) is the automaton \(({R_{1}^{2}}, {{\varSigma }}, \eta ^{2})\) where the transitions are given by

Note that, with this construction, r2r1 acts in the same way when seen as a state of \(\mathcal {A}^{2}\) as when seen as a sequence of states of \(\mathcal {A}\). With this choice, we have that b(D, i) = b− 1a is a state in R and can avoid taking multiple copies of the encoding \(\mathcal {T}_{2}\) over  of \(\mathcal {T}^{\prime }\) from Proposition 11 as we only need the copy for r = b− 1a.
of \(\mathcal {T}^{\prime }\) from Proposition 11 as we only need the copy for r = b− 1a.
As in Example 21, we use ε for α and define \(\beta : \mathbb {N} \to R^{\pm *}\) by
This also yields α0 = ε and β0 (as defined in the proof of Theorem 10). So, effectively, we use Bβ, ε for Bβ, α and \(B_{\beta _{0}, \varepsilon }\) for \(B_{\beta _{0}, \alpha _{0}}\) for the commutators. We continue to abbreviate the former by B and the latter by B0.
We want to reduce the word problem of M (which now is EXPSPACE-complete) to the compressed word problem of \({\mathscr{G}}(\mathcal {T})\). Here, we cannot simply use the same proof as in the case of the (normal) word problem, however! Recall that we have mapped the input word w of length n to the state sequence
In the case using the free group F3 for \({\mathscr{G}}(\mathcal {R})\), we have \(\boldsymbol {b}_{i}^{\prime } = \boldsymbol {p}_{i, b^{-1}a} = \boldsymbol {p}_{i}\) where pi is given by Proposition 11.Footnote 19 In turn, the pi were given by \(f, \boldsymbol {q}_{s(n) - 1}, \dots , \boldsymbol {q}_{0}, \boldsymbol {c}^{\prime }, \boldsymbol {c}_{s(n) - 1}, \dots , \boldsymbol {c}_{0}, z\) and D was (the next power of two after) 3 + 2s(n) in the proof of Proposition 11.
This is a problem since we now have exponentially many ci and qi and we, thus, cannot output all of them with a LOGSPACE (or even polynomial time) transducer – even if we compress every individual ci and qi using a straight-line program. On the positive side, we have that all ci and all except linearly many qi are structurally very similar: we have

for all 0 ≤ i < s(n) and all n + 1 ≤ j < s(n). Due to this structural similarity, we will still be able to output a single straight-line program that generates a word equal to \(B_{0}[\boldsymbol {c}_{s(n) - 1}, \dots , \boldsymbol {c}_{n + 1}]\) in \({\mathscr{G}}(\mathcal {T})\) and one generating a word equal to \(B_{0}[\boldsymbol {q}_{s(n) - 1}, \dots , \boldsymbol {q}_{n + 1}]\) in \({\mathscr{G}}(\mathcal {T})\).
Twisted Balanced Iterated Commutators
For the construction of these straight-line programs, we use a twisted version of our nested commutators, where the left side has an additional conjugation.
Definition 26
Let Q be some alphabet, \(\alpha , \beta : \mathbb {N} \to Q^{\pm *}\) and γ ∈ Q±∗. For p ∈ Q±∗, we define Bβ, α(p, D) inductively for all D = 2d:
The compatibility between commutators and conjugation allows us to use the twisted version to move an iterated conjugation of the commutator entries into the commutator itself. As we have already seen, the check state sequences ci and (most) qi are of this form.
Lemma 27
Let G be a group generated by a finite set Q, \(\alpha , \beta : \mathbb {N} \to Q^{\pm *}\) and γ ∈ Q±∗ such that γ commutes in G with α(d) and β(d) for all d. Furthermore, for some p ∈ Q±∗, let
for 0 ≤ i. Then, we have
for all D = 2d.
Proof
We simply write Bγ for \(B_{\beta , \alpha }^{\gamma }\) and B for Bβ, α and prove the statement by induction on d. For d = 0 (or, equivalently D = 1), we have \(B^{\gamma }[\boldsymbol {p}, 1] = \boldsymbol {p} = \boldsymbol {p}_{0} = B[\boldsymbol {p}_{0}]\) and, for the inductive step from d to d + 1 (or, equivalently, from D to 2D), we have in G:
□
The connection in Lemma 27 allows us to use \(B_{\beta , \varepsilon }^{\gamma }\) for the check sequences ci and qi. The advantage of this approach is that the twisted version can efficiently be compressed into a straight-line program (although the corresponding (ordinary) balanced iterated commutator would have too many entries).
Lemma 28
If the functions α and β are computable in DLINSPACE (where the input is given in binary), we can compute a straight-line program for \(B_{\beta , \alpha }^{\gamma }(\boldsymbol {p}, D)\) with D = 2d on input of p and D in logarithmic space (where D is given in binary).
Proof
The alphabet of the straight-line program is obviously Q± 1 and we only give the variables implicitly. Clearly, if we can compute the production rules for a variable X generating a state sequence q, we can also compute the production rules for a variable X− 1 generating q− 1. Therefore, we only give the positive version for every variable (but always assume that we also have a negative one).
First, we add the production rules
because we need blocks of γ for the recursion of \(B_{\beta , \alpha }^{\gamma }\). Clearly, \(M_{2^{i}}\) generates \(\gamma ^{2^{i}}\) for all 0 ≤ i < d. For the actual commutator, we use the variables \(A_{2^{i}}\) for 0 ≤ i ≤ d and add the production rules
for all 0 ≤ i < d. Using a simple induction it is now easy to see that \(A_{\kern -0.25ex {D}}\) generates \(B_{\beta , \alpha }^{\gamma }[\boldsymbol {p}, D]\) for D = 2d. Accordingly, we choose \(A_{\kern -0.25ex {D}}\) as the start variable.
By assumption, the functions α and β can be computed in DLINSPACE on input of the binary representation of d – this means, the required space is logarithmic in d. To compute the productions rules, we obviously only need to count up to d (in binary) and this can clearly be done in logarithmic space with respect to the binary length of D (which is d). □
With these twisted commutators and the corresponding straight-line programs, we have introduced the missing pieces to adapt the proof for PSPACE and the (normal) word problem from Theorem 10 to EXPSPACE and the compressed word problem.
Proof Proof of Theorem 25
As we have already remarked, we only need to show that the problem is EXPSPACE-hard and construct the \({\mathscr{G}}\)-automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\) from the machine M for an EXPSPACE-complete problem in the same way as in the proof of Theorem 10.
However, compared to the case of the (normal) word problem, we need to make some changes to the reduction of the (normal) word problem of M to the compressed word problem of \({\mathscr{G}}(\mathcal {T})\). We map an input word w of length n for M to a straight-line program for a state sequence q equal toFootnote 20
in \({\mathscr{G}}(\mathcal {T})\). If the Turing machine M accepts the input w, this means (by Proposition 11 and Fact 8) that there is some \(u \in Y^{*} = (\{ 0, 1, \# \} \cup {\varGamma })^{*} \subseteq {{\varSigma }}^{*}\) such that q ⋅ u is in \({\mathscr{G}}(\mathcal {T})\) equal to
(because we have pi ⋅ u$ = r = b− 1a = b(D, i) in this case). The inner commutators are both equal to \(B_{3}(2^{2n^{e}})\) (from Example 21) and, thus, in b− 1{a, b, c}±∗a (and freely reduced). This means that the outer commutator is a non-empty freely reduced word in F3 (as we have already pointed out in Example 21). If the Turing machine does not accept w, we have  in \({\mathscr{G}}(\mathcal {T})\) for some i and the commutators also collapse to the neutral element by Fact 4. This shows that we can use the same argument as in the proof of Theorem 10.
in \({\mathscr{G}}(\mathcal {T})\) for some i and the commutators also collapse to the neutral element by Fact 4. This shows that we can use the same argument as in the proof of Theorem 10.
Thus, it remains to describe how we can compute a straight-line program for such a q in logarithmic space. If we have straight-line programs for the individual entries, we immediately also obtain straight-line programs for their inverses and can combine everything into a straight-line program for the overall nested commutator. This can be done (on the level of the variables) in logarithmic space by Lemma 7. For f, \(\boldsymbol {q}_{n}, \dots , \boldsymbol {q}_{0}\), \(\boldsymbol {c}_{n}, \dots , \boldsymbol {c}_{0}\) and z, we do not even need straight-line programs but can output the words directly (as in the PSPACE-case).
For the inner commutators, recall that we have

for all \(0 \leq i < 2^{2n^{e}}\). Thus, we have

in \({\mathscr{G}}(\mathcal {T})\) by Lemma 27 where we write \(B_{0}^{\checkmark _{\!\!\!\text {id}}}\) for \(B_{\beta _{0}, \alpha _{0}}^{\checkmark _{\!\!\!\text {id}}}\). In order to apply Lemma 27, we need that \(\checkmark _{\!\!\!\text {id}}\) commutes with (ε and) β0(d) for all d. However, this immediately follows from the construction of \(\mathcal {T}\) (as \(\checkmark _{\!\!\!\text {id}}\) only manipulates the TM part of the input word while b0 and c0 only manipulate the commutator part).
Finally, we can compute a straight-line program for the two twisted commutators in LOGSPACE by Lemma 28. Here, it is important that n is the input length and that, thus, \(2^{2n^{e}}\) can be output in binary (since it has length 2ne).
The last remaining part is a straight-line program for
The inner part can be output directly and the outer \(\checkmark _{\!\!\!\text {id}}\)-blocks of length \({2^{2n^{e}}}\) can be generated in the same way as in the proof of Lemma 28.Footnote 21□
We can take the disjoint union of the \({\mathscr{G}}\)-automaton over Σ with a PSPACE-complete word problem and the \({\mathscr{G}}\)-automaton over Σ with an EXPSPACE-complete compressed word problem. In this way, we obtain an automaton group whose (normal) word problem is PSPACE-complete and whose compressed word problem is EXPSPACE-complete and, thus, provably harder (by the space hierarchy theorem [29, Theorem 6], see also e. g. [27, Theorem 7.2, p. 145] or [2, Theorem 4.8]).
Corollary 29
There is an automaton group with a binary alphabet whose word problem
Constant: a \({\mathscr{G}}\)-automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\) with |Σ| = 2
Input: a state sequence q ∈ Q±∗
Question: is
in \({\mathscr{G}}(\mathcal {T})\)?
is PSPACE-complete and whose compressed word problem
Constant: the same \({\mathscr{G}}\)-automaton \(\mathcal {T} = (Q, {{\varSigma }}, \delta )\) with |Σ| = 2
Input: a straight-line program generating a state sequence q ∈ Q±∗
Question: is
in \({\mathscr{G}}(\mathcal {T})\)?
is EXPSPACE-complete.
Notes
In order to avoid ambiguities, we call a word over the states of the automaton a state sequence. So, in our case the input for the word problem is a state sequence.
In fact, the semigroup is generated by a partial, invertible automaton. A priori, this seems to be a stronger statement than that the semigroup is inverse and also an automaton semigroup. That is why the cited paper uses the term “automaton-inverse semigroup”. Only later, it was shown that the two concepts actually coincide [11, Theorem 25].
The usage of commutators to compute Boolean functions has been formalized by the notion of G-programs (see [3]). Here, we do not use this formalism because it cannot be applied to the compressed word problem.
In fact, it would suffice if α and β were computable in space 2n here. However, we will not need this more general statement and the hypothesis is not sufficient when we consider the compressed word problem later on.
That the alphabet may be assumed to contain exactly four elements can be seen easily. In fact, we may even assume it to be of size three or – with suitable encoding – size two.
Typically, DFA is an abbreviation for “deterministic finite automaton”. However, as it is common in the setting of this paper, we use the term automaton to refer to what is more precisely a transducer (we have an output). Therefore, we use the term acceptor to refer to automata without output.
In fact, even the corresponding problem for automaton semigroups is in PSPACE.
In fact, we will need multiple copies of \(\mathcal {T}^{\prime }\) where we replace r by a different state in each copy.
… so they cannot be distinguished algebraically at the moment. We will later replace r with another state to distinguish them.
We do not check that the digit blocks for the check-marking are non-empty here. This is handled implicitly by other states below (namely by \(\checkmark _{\!\!\!r}\) but independently also by c).
including, in particular, A5 from Example 5, which requires an alphabet of size of five.
For the idea to use the free group for a logical conjunction, see also [28].
Technically, the automaton is not synchronous because we use the empty word in some outputs. However, we can emit a special symbol e instead and then map all e s to ε using a homomorphism.
Our definition of uniformly SENS is not exactly the one of [4]: we have changed the ordering of some indices here because it is more convenient for our other definitions.
Compare this to the tree in Fig. 8.
Strictly speaking, we do not have the states ri on the right but rather state sequences from \(\text {id}^{*} r_{i} \text {id}^{*}\). However, we omit these id states from the cross diagram to keep it more readable.
In fact, by the construction of \(\mathcal {T}^{\prime }\), we actually either have \(\boldsymbol {b}_{i}^{\prime } \cdot u \$ = \boldsymbol {b}_{i}\) or
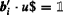 in \({\mathscr{G}}(\mathcal {T})\) for all 0 ≤ i < D.
in \({\mathscr{G}}(\mathcal {T})\) for all 0 ≤ i < D.Again, we actually have state sequences from id∗, rather, but omit them for readability.
Remember that we only have a single copy of \(\mathcal {T}_{2}\) (resp. HCode \(\mathcal {T}^{\prime }\)) this time and, thus, can omit the index r.
To be absolute precise: we actually need to repeat one of the entries of the outer commutator in order to get a power of two as the number of entries.
In fact, we already have the required production rules and variables up to \(M_{2^{2n^{e} - 1}}\).
References
Aleshin, S.V.: A free group of finite automata. Vestnik Moskovskogo Universiteta. Seriya I. Matematika, Mekhanika (4), 12–14 (1983)
Arora, S., Barak, B.: Computational Complexity: A Modern Approach. Cambridge University Press, Cambridge (2009)
Mix Barrington, D.A.: Bounded-width polynomial-size branching programs recognize exactly those languages in NC1. J. Comput. Syst. Sci. 38(1), 150–164 (1989). https://doi.org/10.1016/0022-0000(89)90037-8
Bartholdi, L., Figelius, M., Lohrey, M., Weiß, A.: Groups with ALOGTIME-hard word problems and PSPACE-complete circuit value problems. In: 35th Computational Complexity Conference, CCC 2020, July 28-31, 2020, Saarbrücken, Germany (Virtual Conference), pp. 29:1–29:29. https://doi.org/10.4230/LIPIcs.CCC.2020.29 (2020)
Bartholdi, L., Mitrofanov, I.: The word and order problems for self-similar and automata groups. Groups Geom. Dyn. 14, 705–728 (2020). https://doi.org/10.4171/GGD/560
Bassino, F., Kapovich, I., Lohrey, M., Miasnikov, A., Nicaud, C., Nikolaev, A., Rivin, I., Shpilrain, V., Ushakov, A., Weil, P.: Complexity and Randomness in Group Theory. De Gruyter, Berlin (2020). https://doi.org/10.1515/9783110667028
Berstel, J., Perrin, D., Reutenauer, C.: Codes and Automata, Encyclopedia of Mathematics and its Applications, vol. 129. Cambridge University Press, Cambridge (2010)
Bondarenko, I.V.: Growth of Schreier graphs of automaton groups. Math. Ann. 354 (2), 765–785 (2012). https://doi.org/10.1007/s00208-011-0757-x
Bondarenko, I.V.: The word problem in Hanoi Towers groups. Algebra Discrete Math. 17(2), 248–255 (2014)
Boone, W.W.: The word problem. Ann. Math. 70(2), 207–265 (1959)
D’Angeli, D., Rodaro, E., Wächter, J.Ph.: The structure theory of partial automaton semigroups. Semigroup Forum 101, 51–76 (2020). https://doi.org/10.1007/s00233-020-10114-5
D’Angeli, D., Rodaro, E., Wächter, J.Ph.: On the complexity of the word problem for automaton semigroups and automaton groups. Adv. Appl. Math. 90, 160–187 (2017). https://doi.org/10.1016/j.aam.2017.05.008
Dehn, M.: Über unendliche diskontinuierliche Gruppen. Math. Ann. 71, 116–144 (1911)
Gillibert, P.: Personal Communication (2019)
Gillibert, P.: The finiteness problem for automaton semigroups is undecidable. Int. J. Algebra Comput. 24(01), 1–9 (2014). https://doi.org/10.1142/S0218196714500015
Gillibert, P.: An automaton group with undecidable order and Engel problems. J. Algebra 497, 363–392 (2018). https://doi.org/10.1016/j.jalgebra.2017.11.049
Grigorchuk, R.I.: Burnside’s problem on periodic groups. Funct. Anal. its Appl. 14, 41–43 (1980)
Grigorchuk, R.I., Pak, I.: Groups of intermediate growth: an introduction. L’Enseignement Mathématique 54, 251–272 (2008)
Kozen, D.: Lower bounds for natural proof systems. In: Proc. of the 18th Ann. Symp. on Foundations of Computer Science, FOCS’77, pp 254–266. IEEE Computer Society Press, Providence, Rhode Island (1977)
Krohn, K., Maurer, W.D., Rhodes, J.L.: Realizing complex boolean functions with simple groups. Inf. Control. 9(2), 190–195 (1966). https://doi.org/10.1016/S0019-9958(66)90229-4
Lohrey, M.: The Compressed Word Problem for Groups. Springer Briefs in Mathematics. Springer, Berlin (2014). https://doi.org/10.1007/978-1-4939-0748-9
Makanin, G.S.: Decidability of the universal and positive theories of a free group. Izv. Akad. Nauk SSSR Ser. Mat. 48, 735–749 (1984). Russian; English translation in: Math. USSR Izvestija, 25, 75–88, 1985
Mal’cev, A.I.: On the equation zxyx− 1y− 1z− 1 = aba− 1b− 1 in a free group. Akademiya Nauk SSSR. Sibirskoe Otdelenie. Institut Matematiki Algebra i Logika 1(5), 45–50 (1962)
Maurer, W.D., Rhodes, J.L.: A property of finite simple non-abelian groups. Proc. Am. Math. Soc. 16(3), 552–554 (1965). https://doi.org/10.2307/2034697
Nekrashevych, V.V.: Self-Similar Groups, Mathematical Surveys and Monographs, vol. 117. American Mathematical Society, Providence (2005). https://doi.org/10.1090/surv/117
Novikov, P.S.: On the algorithmic unsolvability of the word problem in group theory. Trudy Mat. Inst. Steklov, pp. 1–143. In Russian (1955)
Papadimitriou, C.M.: Computational Complexity. Addison-Wesley, Boston (1994)
Robinson, D.: Parallel algorithms for group word problems. Ph.D. thesis, University of California, San Diego (1993)
Stearns, R.E., Hartmanis, J., Lewis, P.M.: Hierarchies of memory limited computations. In: 6th Annual Symposium on Switching Circuit Theory and Logical Design (SWCT 1965), pp. 179–190. IEEE (1965)
Steinberg, B.: On some algorithmic properties of finite state automorphisms of rooted trees. Contemporary Mathematics, vol. 633. American Mathematical Society, Providence (2015)
Šunić, Z., Ventura, E.: The conjugacy problem in automaton groups is not solvable. J. Algebra 364, 148–154 (2012). https://doi.org/10.1016/j.jalgebra.2012.04.014
Vorobets, M., Vorobets, Y.: On a free group of transformations defined by an automaton. Geom. Dedicata. 124, 237–249 (2007). https://doi.org/10.1007/s10711-006-9060-5
Wächter, J. Ph.: Automaton structures – decision problems and structure theory. Doctoral thesis, Institut für Formale Methoden der Informatik, Universität Stuttgart. https://doi.org/10.18419/opus-11267 (2020)
Wächter, J.Ph., Weiß, A.: An automaton group with PSPACE-complete word problem. In: 37th International Symposium on Theoretical Aspects of Computer Science, STACS 2020, March 10-13, 2020, Montpellier, France, pp. 6:1–6:17. https://doi.org/10.4230/LIPIcs.STACS.2020.6 (2020)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Armin Weiß was funded by DFG project DI 435/7-1. The research for this article was mainly conducted while Jan Philipp Wächter was affiliated with Universität Stuttgart. During later stages of the publication process, he was partially supported by Centro de Matemática da Universidade do Porto (CMUP), which is financed by Portuguese national funds through FCT - Fundação para a Ciência e Tecnologia, I.P., under the project with reference UIDB/00144/2020.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article belongs to the Topical Collection: Special Issue on Theoretical Aspects of Computer Science (STACS 2020) Guest Editors: Christophe Paul and Markus Bläser
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wächter, J.P., Weiß, A. An Automaton Group with PSPACE-Complete Word Problem. Theory Comput Syst 67, 178–218 (2023). https://doi.org/10.1007/s00224-021-10064-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00224-021-10064-7






 in G?
in G? in
in  in
in 







 in G and
in G and
 in
in  in
in  in
in 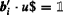 in
in