On sharpness of error bounds for multivariate neural network approximation

Abstract

Single hidden layer feedforward neural networks can represent multivariate functions that are sums of ridge functions. These ridge functions are defined via an activation function and customizable weights. The paper deals with best non-linear approximation by such sums of ridge functions. Error bounds are presented in terms of moduli of smoothness. The main focus, however, is to prove that the bounds are best possible. To this end, counterexamples are constructed with a non-linear, quantitative extension of the uniform boundedness principle. They show sharpness with respect to Lipschitz classes for the logistic activation function and for certain piecewise polynomial activation functions. The paper is based on univariate results in Goebbels (Res Math 75(3):1–35, 2020. https://rdcu.be/b5mKH)

1 Introduction

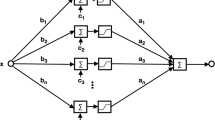
A feedforward neural network with an activation function $\sigma :\mathbb {R}\rightarrow \mathbb {R}$, d input nodes, one output node, and one hidden layer of n neurons implements a multivariate real-valued function $g :\mathbb {R}^d\rightarrow \mathbb {R}$ of type

$$\begin{aligned} g(\mathbf {x}) \in {{\mathcal {M}}}_n&:= {{\mathcal {M}}}_{n,\sigma }:=\left\{ \sum _{k=1}^n a_k \sigma (\mathbf {w}_k \cdot \mathbf {x}+c_k) : a_k, c_k\in \mathbb {R}, \mathbf {w}_k\in \mathbb {R}^d \right\} , \end{aligned}$$

(1)

see Fig. 1. For vectors $\mathbf {w}_k =(w_{k,1},\ldots , w_{k,d})$ and $\mathbf {x}=(x_1,\ldots ,x_d)$,

$$\begin{aligned} \mathbf {w}_k\cdot \mathbf {x}= \sum _{j=1}^d w_{k,j} x_{j} \end{aligned}$$

is the standard inner product of $\mathbf {w}_k,\,\mathbf {x}\in \mathbb {R}^d$. Summands $\sigma (\mathbf {w}_k \cdot \mathbf {x}+c_k)$ are ridge functions. They are constant on hyperplanes $\mathbf {w}_k \cdot \mathbf {x}= c$, $c\in \mathbb {R}$.

Fig. 1

One hidden layer neural network that computes $\sum _{k=1}^n a_k \sigma (\mathbf {w}_k \cdot \mathbf {x}+c_k)$

For non-constant bounded monotonically increasing and continuous activation functions $\sigma$ the universal approximation property holds, see the paper of Funahashi [14]: Given a continuous function f on a compact set then for each $\varepsilon >0$ there exists $n\in \mathbb {N}$ and a function $g_n\in \mathcal{M}_n$ such that the sup-norm of $f-g_n$ is less than $\varepsilon$. Cybenko showed this property in [10] for a different class of continuous activation functions that do not have to be monotone. Leshno et al. proved for continuous activation functions $\sigma$ in [23] (cf. [6]) that the universal approximation property is equivalent to $\sigma$ being not an algebraic polynomial. Continuity is not a necessary prerequisite for the universal approximation property, see [21].

We discuss error bounds for best approximation by functions of ${{\mathcal {M}}}_n$ in terms of moduli of smoothness for an arbitrary number d of input nodes in Sect. 2. These results are quantitative extensions of the qualitative universal approximation property. They introduce convergence orders that depend on the smoothness of functions to be approximated.

Many papers deal with the univariate case $d=1$. In [11], Debao proved an estimate against a first oder modulus for general sigmoid activation functions. An overview of other estimates against first order moduli is given in doctoral thesis [7], cf. [8]. Under additional assumptions on activation functions, estimates against higher order moduli are possible. For example, one can easily extend the first order estimate of Ritter for approximation with “nearly exponential” activation functions in [29] to higher moduli, see [16]. Similar results can be obtained for activation functions that are arbitrarily often differentiable on some open interval such that they are not an algebraic polynomial on that interval, see [28, Theorem 6.8, p. 176] in combination with [16].

With respect to the general multivariate case, Barron applied Fourier methods in [4] to establish a convergence rate for a certain class of smooth functions in the $L^2$-norm. Approximation errors for multi-dimensional bell shaped activation functions were estimated by first order moduli of smoothness or related Lipschitz classes by Anastassiou (e.g. [2]) and Costarelli and Spigler (see e.g. [9] including a literature overview). However, discussed neural network spaces differ from (1). They do not consist of linear combinations of ridge functions. A special network with four layers is introduced in [24] to obtain a Jackson estimate in terms of a first order modulus of smoothness.

Maiorov and Ratsby established an upper bound for functions in Sobolev spaces based on pseudo-dimension in [25, Theorem 2]. Pseudo-dimension is an upper bound of the Vapnik-Chervonenkis dimension (VC dimension) that will also be used in this paper to obtain lower bounds.

With respect to neural network spaces (1) of ridge functions, we apply results of Pinkus [28] and Maiorov and Meir [27] to obtain error bounds for a large class of activation functions either based on K-functional techniques or on known estimates for best approximation with multivariate polynomials in Sect. 2. Both $L^p$- and sup-norms are considered.

In Sect. 3, we prove for the logistic activation function that counterexamples $f_\alpha$ exist for all $\alpha >0$ such that sup-norm as well as $L^p$-norm bounds are in $O(n^{-\alpha })$ but the error of best approximation is not in $O(n^{-\beta })$ for $\beta > \alpha$. This result is a multivariate extension of univariate counterexamples ($d=1$, one single input node, sup-norm) in [16]. A similar result is shown for piecewise polynomial activation functions with respect to an $L^2$-norm bound.

In fact, the non-linear variant of a quantitative uniform boundedness principle in [16] can be applied to construct univariate and multivariate counterexamples. This principle is based on theorems of Dickmeis, Nessel and van Wickeren, cf. [13], that can be used to analyze error bounds of linear approximation processes. Its application, both in a linear and in the given non-linear context, requires the construction of a resonance sequence. To this end, a known result [5] on the VC dimension of networks with logistic activation is used. Theorem 5 in Sect. 3 is formulated as a general means to derive discussed counterexamples from VC dimension estimates. Also, [27] already provides sequences of counterexamples that can be condensed to a single counterexample with the uniform boundedness principle.

There are some published attempts to show sharpness of error bounds for neural network approximation in terms of moduli of smoothness based on inverse theorems. Inverse and equivalence theorems estimate the values of moduli of smoothness by approximation rates. For example, they determine membership to certain Lipschitz classes from known approximation errors. However, the letter [15] proves that the inverse theorem for neural network approximation in [31] as well as the inverse theorems in some related papers are wrong. Smoothness is one feature that favors high approximation rates. But in this non-linear situation, other features (e.g., the “nearly exponential” property or similarity to certain derivatives of the activation function, cf. [22]) also contribute to convergence rates. Such features cannot be sufficiently measured by moduli of smoothness, cf. sequence of counterexamples in [15]. This is the motivation to work with counterexamples instead of inverse or equivalence theorems in Sect. 3.

2 Notation and direct estimates

Let $\varOmega \subset \mathbb {R}^d$ be an open set. By $X^p(\varOmega ):=L^p(\varOmega )$ with norm

$$\begin{aligned} \Vert f\Vert _{L^p(\varOmega )}:=\root p \of {\int _\varOmega |f(\mathbf {x})|^p d\mathbf {x}} \end{aligned}$$

for $1\le p<\infty$ and $X^\infty (\varOmega ):=C(\overline{\varOmega })$ with sup-norm $\Vert f\Vert _{C(\overline{\varOmega })}:=\sup \{|f(\mathbf {x})| : \mathbf {x}\in \overline{\varOmega }\}$ we denote the usual Banach spaces.

For a multi-index $\alpha =(\alpha _1,\ldots ,\alpha _d)\in \mathbb {N}_0^d$ with non-negative integer components, let $|\alpha |:= \sum _{j=1}^d \alpha _j$ be its sum of components. We write $\mathbf {x}^\alpha := \prod _{j=1}^d x_j^{\alpha _j}$. With $P_k$ we denote the set of multivariate polynomials with degree at most k, i.e., each polynomial in $P_k$ is a linear combination of homogeneous polynomials of degree $l\in \{0,\ldots ,k\}$. To this end, let

$$\begin{aligned} H_l:= \left\{ f:\mathbb {R}^d \rightarrow \mathbb {R} : f(\mathbf {x})= \sum _{\alpha \in \mathbb {N}_0^d,\,|\alpha |=l} c_\alpha \mathbf {x}^\alpha \right\} \end{aligned}$$

be the space of homogeneous polynomials of degree l.

The set of all univariate polynomials with degree at most k is denoted by $\varPi _k$, i.e., $\varPi _k=P_k$ for $d=1$. Let

$$\begin{aligned} s:=\dim H_k = \left( {\begin{array}{c}d+k-1\\ k\end{array}}\right) \le (k+1)^{d-1}. \end{aligned}$$

To obtain the upper estimate, we choose exponents $\alpha _1,\ldots ,\alpha _{d-1}$ in $\mathbf {x}^\alpha$ independently from the set $\{0,\ldots ,k\}$. If the sum of these exponents does not exceed k then $\alpha _{d}=k-\sum _{j=1}^{d-1} \alpha _j$. Otherwise, we have counted a polynomial with degree greater than k. Thus, the estimate is a coarse upper bound only.

Multivariate polynomials can be represented by univariate polynomials, cf. [28, p. 164]: for a given degree $k\in \mathbb {N}$ there exist $s\le (k+1)^{d-1}$ vectors $\mathbf {w}_1,\ldots ,\mathbf {w}_s \in \mathbb {R}^d$ such that

$$\begin{aligned} P_k=\left\{ \sum _{j=1}^s p_j(\mathbf {w}_j\cdot \mathbf {x}) : p_j\in \varPi _k \right\} . \end{aligned}$$

(2)

We use the result [28, p. 176], cf. [19]: Let $\sigma :\mathbb {R}\rightarrow \mathbb {R}$ be arbitrarily often differentiable on some open interval $I\subset \mathbb {R}$, i.e. $\sigma \in C^\infty (I)$, and let $\sigma$ be no algebraic polynomial on that interval. Then univariate polynomials of degree at most k can be uniformly approximated arbitrarily well on compact sets by choosing parameters $a_j,b_j,c_j\in \mathbb {R}$ in

$$\begin{aligned}\sum _{j=1}^{k+1} a_j\sigma (b_j x + c_j).\end{aligned}$$

Thus due to (2), also multivariate polynomials of degree at most k can be approximated by functions of ${{\mathcal {M}}}_{s(k+1)}$ arbitrarily well on compact sets, i.e., in the sup-norm

$$\begin{aligned} P_k \subset \overline{{{\mathcal {M}}}_{s(k+1)}}. \end{aligned}$$

(3)

Theorem 3.1 in [22] even describes a more general class of multivariate functions that can be approximated arbitrarily well like polynomials.

There holds following lemma from [19, Proposition 4] that extends (3) to simultaneous approximation.

Lemma 1

Let $\sigma :\mathbb {R}\rightarrow \mathbb {R}$ be arbitrarily often differentiable on an open interval around the origin with $\sigma ^{(i)}(0)\ne 0$, $i\in \mathbb {N}_0$. Then for any polynomial $\pi \in P_k$ of degree at most k, any compact set $I\subset \mathbb {R}^d$, and each $\varepsilon >0$ there exists a sufficiently often differentiable function $g\in {{\mathcal {M}}}_{s(k+1)}$ such that simultaneously for all $\alpha \in \mathbb {N}_0^d$, $|\alpha |\le k$,

$$\begin{aligned} \left\| \frac{\partial ^{|\alpha |}}{\partial x_1^{\alpha _1} \dots \partial x_d^{\alpha _d}} \left( \pi (\mathbf {x}) - g(\mathbf {x})\right) \right\| _{C(I)} < \varepsilon . \end{aligned}$$

The requirement that derivatives at zero must not be zero can be replaced by the requirement that $\sigma$ is no algebraic polynomial on the open interval, see [19].

With n summands of the activation function, polynomials of degree k and their derivatives can be simultaneously approximated arbitrarily well for such values of k that fulfill $n\ge (k+1)^d \text {, i.e.~} k \le \root d \of {n} -1$, because $(k+1)^d = (k+1)^{d-1} (k+1) \ge s(k+1)$. Especially, polynomials of degree at most

$$\begin{aligned} k := \lfloor \root d \of {n} \rfloor -1 \end{aligned}$$

(4)

can be approximated arbitrarily well.

Let $f\in X^p(\varOmega )$, $\mathbf {h}\in \mathbb {R}^d$, $r\in \mathbb {N}_0$ und $t\in \mathbb {R}$. The rth radial difference (with direction $\mathbf {h}$) is given via

$$\begin{aligned} \varDelta _\mathbf {h}^r f(\mathbf {x}) := \sum _{j=0}^r (-1)^{r-j} \left( {\begin{array}{c}r\\ j\end{array}}\right) f(\mathbf {x}+j\mathbf {h}) \end{aligned}$$

(if defined). Thus, $\varDelta _\mathbf {h}^r f=\varDelta _\mathbf {h}^{r-1}\varDelta _\mathbf {h}^1 f =\varDelta _\mathbf {h}^1 \varDelta _\mathbf {h}^{r-1} f$. Let

$$\begin{aligned} \varOmega (\mathbf {h}) := \{\mathbf {x}\in \varOmega : \mathbf {x}+t \mathbf {h}\in \varOmega ,\, 0\le t\le 1\}. \end{aligned}$$

Then the rth radial modulus of smoothness of a function $f\in L^p(\varOmega )$, $1\le p<\infty$, or $f\in C(\overline{\varOmega })$ is defined via

$$\begin{aligned} \omega _r(f,\delta )_{p,\varOmega }&:=\sup \{ \Vert \varDelta _\mathbf {h}^r f \Vert _{X^p(\varOmega (r\mathbf {h}))} : \mathbf {h}\in \mathbb {R}^d,\, |\mathbf {h}|\le \delta \}. \end{aligned}$$

Our aim is to discuss errors E of best approximation. For $S\subset X^p(\varOmega )$ and $f\in X^p(\varOmega )$ let

$$\begin{aligned} E(S, f)_{p,\varOmega } := \inf \{ \Vert f-g\Vert _{X^p(\varOmega )} : g\in S\}. \end{aligned}$$

Thus, $E(S, f)_{p,\varOmega }$ is the distance between f and S.

As an application of a multivariate equivalence theorem between K-functional and moduli of smoothness, an estimate for best polynomial approximation is proved on Lipschitz graph domains (LG-domains) in [20, Corollary 4, p. 139]. For the definition of not necessarily bounded LG-domains, see [1, p. 66]. For bounded domains, the LG property is equivalent to a Lipschitz boundary. Especially, later discussed bounded d-dimensional open intervals like $(0, 1)^d:=(0, 1)\times \dots \times (0, 1)$ and the unit ball $\{\mathbf {x}\in \mathbb {R}^d : |\mathbf {x}|<1\}$ are examples for LG-domains.

Let $\varOmega$ be a bounded LG-domain in $\mathbb {R}^n$ and $1\le p\le \infty$, then

$$\begin{aligned} E(P_k, f)_{p,\varOmega } \le C_r\omega _r\left( f, \frac{1}{k}\right) _{p,\varOmega } \end{aligned}$$

(5)

with a constant $C_r$ that is independent of f and k, see [20].

Theorem 1

(Arbitrarily Often Differentiable Functions) Let $\sigma :\mathbb {R}\rightarrow \mathbb {R}$ be arbitrarily often differentiable on some open interval in $\mathbb {R}$, and let $\sigma$ be no algebraic polynomial on that interval, $f\in X^p(\varOmega )$ for an LG-domain $\varOmega \in \mathbb {R}^d$, $1\le p\le \infty$, and $r\in \mathbb {N}$. For $n\ge 4^d$ there exists a constant C that is independent of f and k such that

$$\begin{aligned} E({{\mathcal {M}}}_n, f)_{p,\varOmega } \le C \omega _r\left( f, \frac{1}{\root d \of {n}} \right) _{p,\varOmega }. \end{aligned}$$

Proof

We combine (3) and (4) with (5) to get

$$\begin{aligned}&E(\mathcal{M}_n, f)_{p,\varOmega } \le C_r \omega _r\left( f,\frac{1}{ \lfloor \root d \of {n} \rfloor -1}\right) _{p,\varOmega }\\&\le C_r \omega _r\left( f,\frac{1}{ \root d \of {n} -2} \right) _{p,\varOmega }\\&\le C_r \omega _r\left( f, \frac{1}{ \root d \of {n} -\frac{\root d \of {n}}{2}} \right) _{p,\varOmega } = C_r \omega _r\left( f, \frac{2}{\root d \of {n}} \right) _{p,\varOmega }\\&\le \underbrace{C_r 2^r}_{C} \omega _r\left( f, \frac{1}{\root d \of {n}} \right) _{p,\varOmega }. \end{aligned}$$

$\square$

By using an error bound for best polynomial approximation we are not able to consider advantages of non-linear approximation. However, we will see in the next section that non-linear neural network approximation does not really perform better than polynomial approximation in the worst case.

Most important activation functions, that are not piecewise polynomials, fulfill the requirements of Theorem 1. For example, it provides an error bound for approximation with the sigmoid activation function based on inverse tangent

$$\begin{aligned} \sigma (x) =\frac{1}{2}+\frac{1}{\pi } \arctan (x), \end{aligned}$$

the logistic function

$$\begin{aligned} \sigma (x) =\frac{1}{1+e^{-x}}=\frac{1}{2}\left( 1+\tanh \left( \frac{x}{2}\right) \right) , \end{aligned}$$

and ”Exponential Linear Unit” (ELU) activation function

$$\begin{aligned} \sigma (x) = \left\{ \begin{array}{ll} \alpha (e^x-1),&{}\quad x<0\\ x ,&{}\quad x\ge 0\end{array}\right. \end{aligned}$$

for $\alpha \ne 0$.

A direct bound for simultaneous approximation of a function and its partial derivatives in the sup-norm can be obtained similarly based on a corresponding estimate for simultaneous approximation by polynomials using a Jackson estimate from [3]:

Lemma 2

Let $f:\mathbb {R}^d \rightarrow \mathbb {R}$ be a function with compact support such that all partial derivatives up to order $k\in \mathbb {N}_0$ are continuous. Let $\overline{\varOmega }\subset \mathbb {R}^d$ be a compact set that contains the support of f. Then there exists a constant $C\in \mathbb {R}$ (independent of n and f) such that for each $n\in \mathbb {N}$ a polynomial $\pi \in P_n$ can be found such that for all $\alpha \in \mathbb {N}_0^d$ with $|\alpha |\le \min \{k, n\}$

$$\begin{aligned}&\left\| \frac{\partial ^{|\alpha |} (f(\mathbf {x})-\pi (\mathbf {x}))}{\partial x_1^{\alpha _1}\dots \partial x_d^{\alpha _d}} \right\| _{C(\overline{\varOmega })}\\&\quad \le \frac{C}{n^{k-|\alpha |}} \max _{\beta \in \mathbb {N}_0^d, |\beta | = k} \omega _1\left( \frac{\partial ^{k} f}{\partial x_1^{\beta _1}\dots \partial x_d^{\beta _d}}, \frac{1}{n}\right) _{\infty ,\varOmega }. \end{aligned}$$

Similar to the proof of Theorem 1, we combine this cited result with Lemma 1 to obtain (cf. [32]).

Theorem 2

(Synchronous Sup-Norm Approximation) Let $\sigma :\mathbb {R}\rightarrow \mathbb {R}$ be arbitrarily often differentiable without being a polynomial. For each function $f:\mathbb {R}^d \rightarrow \mathbb {R}$ with compact support and continuous partial derivatives up to order $k\in \mathbb {N}_0$ and each compact set $\overline{\varOmega }\subset \mathbb {R}^d$ containing the support of f following estimate holds true: For each $n\in \mathbb {N}$, $n\ge 4^d$, there exists a constant $C\in \mathbb {R}$ (independent of n and f) such that for all $\alpha \in \mathbb {N}_0^d$ with $|\alpha |\le \min \{k, \root d \of {n} -1\}$

$$\begin{aligned}&\inf \left\{ \left\| \frac{\partial ^{|\alpha |} (f(\mathbf {x})-g(\mathbf {x}))}{\partial x_1^{\alpha _1}\dots \partial x_d^{\alpha _d}} \right\| _{C(\overline{\varOmega })} : g\in {{\mathcal {M}}}_n\right\} \nonumber \\&\;\qquad \le \frac{C}{n^{\frac{k-|\alpha |}{d}}} \max _{\beta \in \mathbb {N}_0^d, |\beta | = k} \omega _1\left( \frac{\partial ^{k} f}{\partial x_1^{\beta _1}\dots \partial x_d^{\beta _d}}, \frac{1}{\root d \of {n}}\right) _{\infty ,\varOmega }. \end{aligned}$$

(6)

Requirements of Theorems 1 and 2 are not fulfilled for activation functions that are of type

$$\begin{aligned} \sigma (x) = \left\{ \begin{array}{cl} 0,&{}\quad x<0\\ x^k, &{}\quad x\ge 0\end{array}\right. \end{aligned}$$

(7)

for $k\in \mathbb {N}$. The often used ReLU function is obtained for $k=1$. Corollary 6.11 in [28, p. 178] is an $L^2$-norm Jackson estimate for this class of functions. To work with this estimate, we need to introduce Sobolev spaces.

Let $W_p^{r}(\varOmega )$, $1\le p< \infty$, be the $L^p$-Sobolev space of r-times (in the weak sense) partially differentiable functions on $\varOmega \subset \mathbb {R}^d$ with semi-norms

$$\begin{aligned} |f|_{W_p^{r}(\varOmega )} = \sum _{\alpha \in \mathbb {N}_0^d : |\alpha | = r} \left\| \frac{\partial ^r f}{\partial x_1^{\alpha _1}\dots \partial x_d^{\alpha _d}} \right\| _{L^p(\varOmega )} \end{aligned}$$

and norm $\Vert f\Vert _{W_p^{r}(\varOmega )} = \sum _{k=0}^r |f|_{W_p^{r}(\varOmega )}$. For r-times continuously differentiable functions f (case $p=\infty$) or functions $f\in W_p^{r}(\varOmega )$ on LG-domains $\varOmega$, $1\le p<\infty$, the estimate

$$\begin{aligned} \omega _r(f,\delta )_{p,\varOmega } \le C_r \delta ^r \sum _{\alpha \in \mathbb {N}_0^d : |\alpha |=r} \left\| \frac{\partial ^r f}{\partial x_1^{\alpha _1}\dots \partial x_d^{\alpha _d}} \right\| _{X^p(\varOmega )} \end{aligned}$$

(8)

holds true, see [20].

According to the Jackson estimate for activation functions (7) in [28, p. 178], let $d\ge 2$ and $\varOmega \subset \mathbb {R}^d$ be the d-dimensional unit ball. Then there exists a constant $C>0$ such that for all $f\in W_2^{r}(\varOmega )$ with $\Vert f\Vert _{W_2^{r}(\varOmega )}\le 1$ and $r\in \mathbb {N}$ with $r<k+1+\frac{d-1}{2}$ (k being the exponent in (7))

$$\begin{aligned} E({{\mathcal {M}}}_n, f)_{2,\varOmega } \le C \frac{1}{n^\frac{r}{d}}. \end{aligned}$$

Thus, for all $f\in W_2^{r}(\varOmega )$ without restriction $\Vert f\Vert _{W_2^{r}(\varOmega )}\le 1$ there holds true $E({{\mathcal {M}}}_n, f)_{2,\varOmega } \le C \Vert f\Vert _{W_2^{r}(\varOmega )} n^{-\frac{r}{d}}$. Due to [1, p. 75], a constant $C_1$ exists independently of f such that $\Vert f\Vert _{W_2^{r}(\varOmega )} \le C_1[\Vert f\Vert _{L^2(\varOmega )} + |f|_{W_2^{r}(\varOmega )}]$. Together we obtain

$$\begin{aligned} E({{\mathcal {M}}}_n, f)_{2,\varOmega } \le C \left[ \Vert f\Vert _{L^2(\varOmega )}+|f|_{W_2^{r}(\varOmega )}\right] \frac{1}{n^\frac{r}{d}}. \end{aligned}$$

(9)

This estimate can be extended to moduli of smoothness using K-functional techniques. To this end, we introduce some definitions that will also be needed in the next section for discussing sharpness. A functional T on a normed space X, i.e., T maps X into $\mathbb {R}$, is non-negative-valued, sub-linear, and bounded, iff for all $f,g\in X,\, c\in \mathbb {R}$

$$\begin{aligned}&T(f) \ge 0,\\&T(f+g) \le T(f) + T(g),\\&T(c f) = |c|T(f),\\&\Vert T\Vert _{X^\sim } := \sup \{ T(f) : f\in X,\, \Vert f\Vert _X\le 1\} < \infty . \end{aligned}$$

The set $X^\sim$ consists of all non-negative-valued, sub-linear, bounded functionals T on X.

Since we deal with non-linear approximation, error functionals will not be sub-linear. Instead we discuss remainders $(E_{n})_{n=1}^\infty$, $E_n : X\rightarrow [0,\infty )$ that fulfill following conditions for $m\in \mathbb {N}$, $f, f_1, f_2,\ldots , f_m\in X$, and constants $c\in \mathbb {R}$:

$$\begin{aligned}&E_{m\cdot n}\left( \sum _{k=1}^m f_k\right) \le \sum _{k=1}^m E_n(f_k), \end{aligned}$$

(10)

$$\begin{aligned}&E_n(cf) = |c| E_n(f), \end{aligned}$$

(11)

$$\begin{aligned}&E_n(f) \le D_n \Vert f\Vert _X, \end{aligned}$$

(12)

$$\begin{aligned}&E_n(f) \ge E_{n+1}(f). \end{aligned}$$

(13)

Constant $D_n$ is independent of f. These conditions are fulfilled for $E_n(f):=E({{\mathcal {M}}}_n, f)_{p,\varOmega }$.

Lemma 3

(K-functional) Let functionals $(E_{n})_{n=1}^\infty$, $E_n : X\rightarrow [0,\infty )$ fulfill (10) and (13). The functionals should also fulfill not only (12) but a stability inequality: Let constant $D_n$ in (12) be independent of n, i.e.,

$$\begin{aligned} E_n(f) \le D_0 \Vert f\Vert _{X} \end{aligned}$$

(14)

for a constant $D_0>0$ and all $n\in \mathbb {N}$. Also, a Jackson-type inequality ($0<\varphi (n)\le 1$)

$$\begin{aligned} E_n(g) \le D_1 \varphi (n) [\Vert g\Vert _X + |g|_U], \end{aligned}$$

(15)

$D_1>0$, is required that holds for all functions g in a subspace $U\subset X$ with semi-norm $|\cdot |_U$. For $n\ge 2$ and a constant $D_2>0$, the sequence $(\varphi (n))_{n=1}^\infty$ has to fulfill

$$\begin{aligned} \varphi \left( \left\lfloor \frac{n}{2}\right\rfloor \right) \le D_2 \varphi (n). \end{aligned}$$

(16)

Via the Peetre K-functional

$$\begin{aligned} K\left( \delta , f, X,U\right) := \inf \{ \Vert f-g\Vert _X + \delta |g|_U : g\in U\} \end{aligned}$$

one can estimate

$$\begin{aligned} E_n(f) \le C\left[ K\left( \varphi (n) , f, X, U\right) + \varphi (n) \Vert f\Vert _X\right] \end{aligned}$$

for $n\ge 2$ with a constant C that is independent of f and n.

Proof

Let $g\in U$. Then

thus for $n\ge 2$:

$\square$

We apply the lemma to (9) with $X=L^2(\varOmega )$, $U=W_2^r(\varOmega )$, $\varphi (n)=n^{-\frac{r}{d}}$. Error functional $E(\mathcal{M}_n, f)_{2,\varOmega }$ fulfills all prerequisites. In connection with the equivalence between K-functionals and moduli of smoothness [20, p. 120] we get

Theorem 3

(Piecewise Polynomial Functions) Let $d\ge 2$, $\varOmega \subset \mathbb {R}^d$ be the d-dimensional unit ball and $\sigma$ a piecewise polynomial activation function of type (7). Constants $C_1, C_2\in \mathbb {R}$ exist such that for each $f\in L^2(\varOmega )$, $n\ge 2$, $r<k+1+\frac{d-1}{2}$:

$$\begin{aligned} E({{\mathcal {M}}}_n, f)_{2,\varOmega }&\le C_1 \left[ K\left( \frac{1}{n^\frac{r}{d}}, f, L^2(\varOmega ), W_2^r(\varOmega ) \right) + \frac{1}{n^\frac{r}{d}} \Vert f\Vert _{L^2(\varOmega )}\right] \nonumber \\&\le C_2 \left[ \omega _r\left( f, \frac{1}{\root d \of {n}} \right) _{2,\varOmega }+ \frac{1}{n^\frac{r}{d}} \Vert f\Vert _{L^2(\varOmega )}\right] . \end{aligned}$$

(17)

The saturation order of the modulus is $n^{-\frac{r}{d}}$, so term $n^{-\frac{r}{d}} \Vert f\Vert _{L^2(\varOmega )}$ is only technical. The estimate also holds for ReLU ($k=1$) with only one ($d=1$) input node for $r=2$, see [16]. It can be extended to the cut activation function because cut can be written as a difference of ReLU and translated ReLU.

3 Sharpness due to counterexamples

A coarse lower estimate can be obtained for all integrable activation functions in the $L^2$-norm based on an estimate for ridge functions in [26]. However, the general setting leads to an exponent $\frac{r}{d-1}$ instead of $\frac{r}{d}$.

The space of all measurable, real-valued functions that are integrable on every compact subset of $\mathbb {R}$ is denoted by $L(\mathbb {R})$.

Lemma 4

Let $\sigma$ be an arbitrary activation function in $L(\mathbb {R})$ and $r\in \mathbb {N}$, $d\ge 2$. Let $\varOmega$ be the d-dimensional unit ball.

Then there exists a sequence $(f_n)_{n=1}^\infty$, $f_n\in W_2^{r}(\varOmega )$, with $\Vert f_n\Vert _{W_2^{r}(\varOmega )}\le C_0$, and a constant $c>0$ such that (cf. Theorem 1)

$$\begin{aligned} \omega _r\left( f_n, \frac{1}{\root d \of {n}}\right) _{2,\varOmega } = {O}\left( \frac{1}{n^{\frac{r}{d}}}\right) \text {~and~~} E({{\mathcal {M}}}_n, f_n)_{2, \varOmega } \ge \frac{c}{n^{\frac{r}{d-1}}}. \end{aligned}$$

Proof

This is a direct corollary of Theorem 1 in [26]: For $A\subset \mathbb {R}^d$ with cardinality |A| let R(A) be the linear space that is spanned by all functions $h(\mathbf {w}\cdot \mathbf {x})$, $h\in L(\mathbb {R})$, $\mathbf {w}\in A$. Thus in contrast to one activation function, different nearly arbitrary functions h are allowed to be used with different vectors $\mathbf {w}$ in linear combinations. Let $\mathcal{R}_n :=\bigcup _{A\subset \mathbb {R}^d : |A|\le n} R(A)$ be the space of functions that can be represented as $\sum _{k=1}^n a_k h_k(\mathbf {w}_k\cdot \mathbf {x})$, $a_k\in \mathbb {R}$, $h_k\in L(\mathbb {R})$, $\mathbf {w}_k\in \mathbb {R}^d$. Then for all activation functions $\sigma \in L(\mathbb {R})$ one has $h_k(x):=\sigma (x+c_k)\in L(\mathbb {R})$ for $c_k\in \mathbb {R}$, i.e. ${{\mathcal {M}}}_n\subset {{\mathcal {R}}}_n$. According to [26], for $d\ge 2$ there exist constants $0<c\le C$ independently of n such that

$$\begin{aligned} \frac{c}{n^{\frac{r}{d-1}}} \le \sup _{f\in W_2^{r}(\varOmega ), \Vert f\Vert _{W_2^{r}(\varOmega )}\le C_0} \inf _{h\in {{\mathcal {R}}}_n} \Vert f-h\Vert _{L^2(\varOmega )} \le \frac{C}{n^{\frac{r}{d-1}}}. \end{aligned}$$

From this condition, we obtain functions $f_n\in W_2^{r}(\varOmega )$, $\Vert f_n\Vert _{W_2^{r}(\varOmega )}\le C_0$, such that

$$\begin{aligned} \frac{1}{2}\frac{c}{n^{\frac{r}{d-1}}}&\le \inf _{h\in {{\mathcal {R}}}_n} \Vert f_n -h\Vert _{L^2(\varOmega )} \le \inf _{h\in \mathcal{M}_n} \Vert f_n -h\Vert _{L^2(\varOmega )} = E({{\mathcal {M}}}_n, f_n)_{2, \varOmega }, \end{aligned}$$

and (see (8))

$$\begin{aligned} \omega _r\left( f_n, \frac{1}{\root d \of {n}}\right) _{2,\varOmega }&\le C_1 \frac{1}{n^\frac{r}{d}} \sum _{\alpha \in \mathbb {N}_0^d : |\alpha |=r}\left\| \frac{\partial ^r f_n}{\partial x_1^{\alpha _1}\dots \partial x_d^{\alpha _d}} \right\| _{L^2(\varOmega )} \le C_2(r,d) \frac{1}{n^\frac{r}{d}}. \end{aligned}$$

$\square$

By considering properties of the activation function, better lower estimates are possible. For the logistic activation function and activation functions that are splines of fixed polynomial degree with finite number of knots like (7), Maiorov and Meir showed that there exists a sequence $(f_n)_{n=2}^\infty$, $f_n\in W_p^{r}(\varOmega )$, $r\in \mathbb {N}$, with $\Vert f_n\Vert _{W_p^{r}(\varOmega )}$ uniformly bounded, and a constant $c>0$ (independent of $n\ge 2$) such that (see [27, Theorems 4 and 5, p. 99, Corollary 2, p. 100])

$$\begin{aligned} E({{\mathcal {M}}}_n, f_n)_{p, \varOmega } \ge \frac{c}{(n\log _2(n))^{\frac{r}{d}}} \end{aligned}$$

(18)

for $1\le p< \infty$ (and $L^\infty (\varOmega )$, but we consider $C(\overline{\varOmega })$ due to the definition of moduli of smoothness). Without explicitly saying so, the proof is based on a VC dimension argument similar to the proof of Theorem 5 that follows in this section. It uses [27, Lemma 7, p. 99]. The formula in line 4 on page 98 of [27] shows that (by choosing parameter m as in the proof of [27, Theorem 4]) one additionally has

$$\begin{aligned} \Vert f_n\Vert _{L^p(\varOmega )}&\le \frac{C}{(n\log _2(n))^{\frac{r}{d}}} = \frac{C}{(n(1+\log _2(n)))^{\frac{r}{d}}} \left[ \frac{1+\log _2(n)}{\log _2(n)}\right] ^{\frac{r}{d}}\nonumber \\&\le \frac{2^{\frac{r}{d}} C }{(n(1+\log _2(n)))^{\frac{r}{d}}}. \end{aligned}$$

(19)

This result was proved for $\varOmega$ being the unit ball. But similar to Theorem 5 below, a grid is used that can also be adjusted to $\varOmega =(0, 1)^d$.

We now apply a resonance principle from [16] that is a straight-forward extension of a general theorem by Dickmeis, Nessel and van Wickern, see [13]. With this principle, we condense sequences $(f_n)_{n=1}^\infty$ like the one in (18) to single counterexamples.

To measure convergence rates, abstract moduli of smoothness $\omega$ are often used, see [30, p. 96ff]. An abstract modulus of smoothness is a continuous, increasing function $\omega : [0,\infty ) \rightarrow [0,\infty )$ such that for $\delta _1,\delta _2 > 0$

$$\begin{aligned} 0=\omega (0)<\omega (\delta _1)\le \omega (\delta _1+\delta _2) \le \omega (\delta _1)+\omega (\delta _2). \end{aligned}$$

(20)

Typically, Lipschitz classes are defined via $\omega (\delta ):=\delta ^\alpha$, $0 < \alpha \le 1$.

Theorem 4

(Adapted Uniform Boundedness Principle, see [16]) Let $(E_{n})_{n=1}^\infty$ be a sequence of remainders that map elements of a real Banach space X to non-negative numbers, i.e.,

$$\begin{aligned}E_n : X\rightarrow [0,\infty ).\end{aligned}$$

The sequence has to fulfill conditions (10)–(13). Also, a family of sub-linear bounded functionals $S_\delta \in X^\sim$ for all $\delta >0$ is given. These functionals will represent moduli of smoothness. To express convergence rates, let

$$\begin{aligned} \mu : (0,\infty )\rightarrow (0,\infty ) \text { and } \varphi : [1,\infty )\rightarrow (0,\infty ) \end{aligned}$$

be strictly decreasing with $\lim _{x\rightarrow \infty } \varphi (x)=0$. Since remainder functionals $E_n$ are not required to be sub-linear, $\varphi$ also has to fulfill following condition. For each $0<\lambda <1$ there has to be a real number $X_0=X_0(\lambda )\ge \lambda ^{-1}$ and constant $C_\lambda >0$ such that for all $x>X_0$ there holds

$$\begin{aligned} \varphi (\lambda x)\le C_\lambda \varphi (x). \end{aligned}$$

(21)

If test elements $h_n\in X$ and a number $n_0\in \mathbb {N}$ exist such that for all $n\in \mathbb {N}$ with $n\ge n_0$ and for all $\delta >0$

$$\begin{aligned} \Vert h_n\Vert _X&\le C_1, \end{aligned}$$

(22)

$$\begin{aligned} S_\delta (h_n)&\le C_2 \min \left\{ 1,\frac{\mu (\delta )}{\varphi (n)} \right\} , \end{aligned}$$

(23)

$$\begin{aligned} E_{4n}(h_n)&\ge c_{3} >0, \end{aligned}$$

(24)

then for each abstract modulus of smoothness $\omega$ satisfying (20) and

$$\begin{aligned} \lim _{\delta \rightarrow 0+}\frac{\omega (\delta )}{\delta }=\infty \end{aligned}$$

(25)

a counterexample $f_\omega \in X$ exists such that

$$\begin{aligned} S_\delta (f_\omega )&= {O}\left( \omega (\mu (\delta ))\right) \text { for } \delta \rightarrow 0+ \end{aligned}$$

and

$$\begin{aligned}&E_{n}(f_\omega ) \not = o(\omega (\varphi (n)))\text { for } n\rightarrow \infty \text {, i.e., } \limsup _{n\rightarrow \infty } \frac{E_{n}(f_\omega )}{\omega (\varphi (n))} > 0. \end{aligned}$$

When dealing with the sup-norm, one can generally apply the resonance theorem in connection with known VC dimensions of indicator functions. The general definition of VC dimension based on sets is as follows.

Let X be a finite set and ${{\mathcal {A}}}\subset {{\mathcal {P}}}(X)$ a family of subsets of X. Set $S\subset X$ is said to be shattered by ${{\mathcal {A}}}$ iff each subset $B\subset S$ can be represented as $B=S\cap A$ for a family member $A\in {{\mathcal {A}}}$. Thus, the set $\{S\cap A : A\in {{\mathcal {A}}}\}$ has $2^{|S|}$ elements, |S| denoting the cardinality S.

$$\begin{aligned} {\text {VC-dim}}({{\mathcal {A}}}) := \sup \{&k\in \mathbb {N} : \exists S\subset X \text { with cardinality }\\&|S|=k \text { such that } S \text { is shattered by } {{\mathcal {A}}}\} \end{aligned}$$

is called the VC dimension of ${{\mathcal {A}}}$.

For our purpose, we discuss a (non-linear) set V of functions $g:X\rightarrow \mathbb {R}$ on a set $X\subset \mathbb {R}^m$. Using Heaviside-function $H:\mathbb {R}\rightarrow \{0, 1\}$,

$$\begin{aligned} H(x)&:= \left\{ \begin{array}{cc}0,&{}\quad x<0\\ 1,&{}\quad x\ge 0,\end{array}\right. \end{aligned}$$

let

$$\begin{aligned} {{\mathcal {A}}} := \{ A\subset X : \exists g\in V :&\, (\forall x\in A: H(g(x))=1)\, \wedge \, (\forall x\in X\setminus A: H(g(x))=0) \}. \end{aligned}$$

Then one typically defines ${\text {VC-dim}}(V):={\text {VC-dim}}({{\mathcal {A}}})$. Thus, $k:={\text {VC-dim}}(V)$ is the largest cardinality of a subset $S=\{x_1, \dots , x_k\}\subset X$ such that for each sign sequence $s_1,\ldots , s_k\in \{-1, 1\}$ a function $g\in V$ can be found that fulfills (cf. [5])

$$\begin{aligned} H(g(x_i)) = H(s_i),\quad 1\le i\le k. \end{aligned}$$

Theorem 5

(Sharpness due to VC Dimension) Let $(V_n)_{n=1}^\infty$ be a sequence of (non-linear) function spaces $V_n$ of bounded real-valued functions on $[0, 1]^d$ such that

$$\begin{aligned} E_n(f):=\inf \{ \Vert f-g\Vert _{C([0, 1]^d)} : g\in V_n\} \end{aligned}$$

(26)

fulfills conditions (10)–(13) on Banach space $C([0, 1]^d)$. An equidistant grid $X_n\subset [0, 1]^d$ with a step size $\frac{1}{\tau (n)}$, $\tau :\mathbb {N} \rightarrow \mathbb {N}$, is given via

$$\begin{aligned} X_{n}:=\left\{ \frac{j}{\tau (n)} : j\in \{0, 1,\ldots ,\tau (n)\}\right\} \times \dots \times \left\{ \frac{j}{\tau (n)} : j\in \{0, 1,\ldots ,\tau (n)\}\right\} . \end{aligned}$$

Let

$$\begin{aligned} V_{n,\tau (n)} := \{ h:X_n\rightarrow \mathbb {R} : \text { a function } g\in V_n \text { exists with } h(\mathbf {x})=g(\mathbf {x}) \text { for all } \mathbf {x}\in X_n \} \end{aligned}$$

be the set of functions that are generated by restricting functions of $V_n$ to this grid. As in Theorem 4, convergence rates are expressed via a function $\varphi (x)$ that fulfills the requirements of Theorem 4 including condition (21). Let VC dimension of $V_{n,\tau (n)}$ and function values of $\tau$ and $\varphi$ be coupled via inequalities

$$\begin{aligned} {\text {VC-dim}}(V_{n,\tau (n)})< & {} [\tau (n)]^d, \end{aligned}$$

(27)

$$\begin{aligned} \tau (4n)\le & {} \frac{C}{\varphi (n)}, \end{aligned}$$

(28)

for all $n\ge n_0\in \mathbb {N}$ with a constant $C>0$ that is independent of n.

Then, for $r\in \mathbb {N}$ and each abstract modulus of smoothness $\omega$ satisfying (20) and (25), there exists a counterexample $f_{\omega }\in C([0, 1]^d)$ such that for $\delta \rightarrow 0+$ and $n\rightarrow \infty$

$$\begin{aligned} \omega _r(f_{\omega }, \delta )_{\infty ,(0, 1)^d} = {O}\left( \omega (\delta ^r)\right) \text { and } E_n(f_{\omega }) \ne o\left( \omega \left( [\varphi (n)]^r\right) \right) . \end{aligned}$$

Proof

Condition (27) implies for $4n\ge n_0$ that a sequence of signs $s_{\mathbf {z}}\in \{-1, 1\}$ for points $\mathbf {z}\in X_{4n}$ exists such that no function in $V_{4n}$ can reproduce the sign of the sequence in each point of $X_{4n}$, i.e., for each $g\in V_{4n}$ there exists a point $\mathbf {z}_0 \in X_{4n}$ such that

$$\begin{aligned} H(g(\mathbf {z}_0)) \ne H(s_{\mathbf {z}_0}). \end{aligned}$$

Based on this sign sequence, we construct an arbitrarily often partially differentiable resonance function $h_n$ such that its function values equal the signs on the grid $X_{4n}$. To this end, we use the arbitrarily often differentiable function

$$\begin{aligned} h(x) := \left\{ \begin{array}{ll} \exp \left( 1-\frac{1}{1-x^2}\right) &{} \text {for } |x|<1,\\ 0 &{} \text {for } |x|\ge 1, \end{array}\right. \end{aligned}$$

with properties $h(0)=1$ and $\Vert h\Vert _{B(\mathbb {R})}=1$. Based on h, we define $h_n$:

$$\begin{aligned} h_n(\mathbf {x}):= \sum _{\mathbf {z}\in X_{4n}} s_{\mathbf {z}} \cdot \prod _{k=1}^d h\left( 2\cdot \tau (4n)\cdot \left( \mathbf {x}_k-\mathbf {z}_k\right) \right) . \end{aligned}$$

Scaling factors $2\cdot \tau (4n)$ are chosen such that supports of summands only intersect at their borders. Therefore, $\Vert h_n\Vert _{C([0, 1]^d)}\le 1$ and $h_n(\mathbf {z})=s_{\mathbf {z}}$ for all $\mathbf {z}\in X_{4n}$.

All partial derivatives of order up to r are in $O([\varphi (n)]^{-r})$ because of (28). Additionally to $h_n$, we choose parameters in Theorem 4 as follows:

$$\begin{aligned}&X=C([0, 1]^d)\text {, } S_\delta (f) := \omega _r(f, \delta )_{\infty ,(0, 1)^d}\text {, } \mu (\delta ):=\delta ^r\text {,} \end{aligned}$$

and $E_n(f)$ as in (26). We do not directly use $\varphi (x)$ with Theorem 4. Instead, function $[\varphi (x)]^r$ fulfills the requirements of the function also called $\varphi (x)$ in Theorem 4.

Requirements (22) and (23) can be easily shown due to the sup-norms of $h_n$ and its partial derivatives, cf. (8).

Resonance condition (24) is fulfilled due to the definition of $h_n$: For each $g\in V_{4n}$ there exits at least one point $\mathbf {z}_0\in X_{4n}$ such that

$$\begin{aligned} H(g(\mathbf {z}_0))\ne H(s_{\mathbf {z}_0})=H(h_n(\mathbf {z}_0)). \end{aligned}$$

Function $h_n$ is defined to fulfill $|h_n(\mathbf {z}_0)|=|s_{\mathbf {z}_0}|=1$. Thus,

$$\begin{aligned} \Vert h_n-g\Vert _{C([0, 1]^d)} \ge |h_n(\mathbf {z}_0)-g(\mathbf {z}_0)| \ge 1, \end{aligned}$$

and $E_{4n} h_n \ge 1$.

All preliminaries of Theorem 4 are fulfilled such that counterexamples exist as stated.$\square$

Theorem 6

(Sharpness for Logistic Function Approximation in Sup-Norm) Let $\sigma$ be the logistic function and $r\in \mathbb {N}$. For each abstract modulus of smoothness $\omega$ satisfying (20) and (25), a counterexample $f_{\omega }\in C([0, 1]^d)$ exists such that for $\delta \rightarrow 0+$

$$\begin{aligned} \omega _r(f_{\omega }, \delta )_{\infty ,(0, 1)^d} = {O}\left( \omega (\delta ^{r})\right) \end{aligned}$$

and for $n\rightarrow \infty$

$$\begin{aligned} E({{\mathcal {M}}}_n, f_{\omega })_{\infty , (0, 1)^d} \ne o\left( \omega \left( \frac{1}{(n [1+\log _2(n)])^{\frac{r}{d}}}\right) \right) . \end{aligned}$$

For univariate approximation, i.e., $d=1$, the theorem is proved in [16]. This proof can be generalized as follows.

Proof

Let $D\in \mathbb {N}$. In [5], an upper bound for the VC dimension of function spaces

$$\begin{aligned} \varDelta _n:= & {} \big \{g : \{-D,-D+1,\ldots , D\}^d \rightarrow \mathbb {R} :\\&\qquad g(x)=a_0+ \sum _{k=1}^{n} a_k \sigma (\mathbf {w}_k \cdot \mathbf {x}+c_k)\text {, } a_0,a_k,c_k\in \mathbb {R}, \mathbf {w}_k\in \mathbb {R}^d\big \} \end{aligned}$$

is derived. Functions are defined on a discrete set with $(2D+1)^d$ points. Please note that the constant function $a_0$ is not consistent with the definition of ${{\mathcal {M}}}_n$. It provides an additional degree of freedom.

We apply Theorem 2 in [5]: There exists $n^*\in \mathbb {N}$ such that for all $n\ge n^*$ the VC dimension of $\varDelta _n$ is upper bounded by

$$\begin{aligned} 2 \cdot (nd +2n+1) \cdot \log _2 (24e(nd+2n+1)D), \end{aligned}$$

i.e., there exists an $n_0\ge \max \{2, n^*\}$, $n_0\in \mathbb {N}$, and a constant $C_d>0$, dependent on d, such that for all $n\ge n_0$

$$\begin{aligned} {\text {VC-dim}}(\varDelta _n) \le C_d\, n[\log _2(n) + \log _2(D)]. \end{aligned}$$

Let constant $E>1$ be chosen such that

$$\begin{aligned} \frac{1+\log _2(E)}{E}< \frac{1}{4C_d}\text {, i.e, } 4C_d [1+\log _2(E)] < E. \end{aligned}$$

(29)

This is possible because

$$\begin{aligned} \lim _{E\rightarrow \infty } \frac{1+\log _2(E)}{E}=0. \end{aligned}$$

Now we choose a suitable value of $D=D(n)$ such that the VC dimension of $\varDelta _n$ is less than $[D(n)]^d$. To this end, let

$$\begin{aligned} D=D(n):= \left\lfloor \root d \of {En(1+\log _2(n))}\right\rfloor . \end{aligned}$$

Then we get for $n\ge n_0$ with (29):

$$\begin{aligned} {\text {VC-dim}}(\varDelta _n)\le & {} C_d\, n[\log _2(n) + \log _2(\root d \of {E n(1+\log _2(n))} )]\\= & {} C_d\, n[\log _2(n) + d^{-1} \log _2(E n(1+\log _2(n)) )]\\\le & {} C_d\, n[2\log _2(n) + \log _2(E) +\log _2(2\log _2(n)) )]\\\le & {} C_d\, n[3\log _2(n) + \log _2(E) + 1 )] \le 4C_d\, n\log _2(n)[1+\log _2(E)]\\< & {} E n\log _2(n) \le \left\lfloor \root d \of { E n(1+\log _2(n))} \right\rfloor ^d = [D(n)]^d. \end{aligned}$$

One can map interval $[-D, D]^d$ to $[0, 1]^d$ with an affine transform. By also omitting constant $a_0$, we estimate the VC dimension of $V_{n,\tau (n)}$ with parameters $V_n:={{\mathcal {M}}}_n$ and $\tau (n):=2D(n):$

$$\begin{aligned} {\text {VC-dim}}(V_{n,\tau (n)})< [D(n)]^d < [2D(n)]^d = [\tau (n)]^d. \end{aligned}$$

Thus, (27) is fulfilled. Conditions (10)–(13) are chosen such that they fit with error functionals

$$\begin{aligned}E_n:=E(\mathcal{M}_n, \cdot )_{\infty , (0, 1)^d}.\end{aligned}$$

For strictly decreasing function

$$\begin{aligned} \varphi (x):=1/\root d \of {x[1+\log _2(x)]} \end{aligned}$$

conditions $\lim _{x\rightarrow \infty } \varphi (x) = 0$ and (21) hold. Latter can be shown for $x>X_0(\lambda ):=\lambda ^{-2}$ because $\log _2(\lambda ) > -\log _2(x)/2$ and

$$\begin{aligned} \varphi (\lambda x)&=\frac{1}{\root d \of {\lambda }} \frac{1}{\root d \of {x(1+\log _2(x)+\log _2(\lambda ))}} \le \frac{1}{\root d \of {\lambda }} \frac{1}{\root d \of {x(1+\frac{1}{2}\log _2(x))}} < \root d \of {\frac{2}{\lambda }} \varphi (x). \end{aligned}$$

Finally, (28) follows from

$$\begin{aligned} \tau (4n)&= 2D(4n) \le 2\root d \of {E4n(1+\log _2(4n))} < \frac{2\root d \of {4E(1+\log _2(4))}}{\varphi (n)} =\frac{2\root d \of {12E}}{\varphi (n)}. \end{aligned}$$

Thus, Theorem 5 can be applied to obtain the counterexample.$\square$

The theorem can also be proved based on the sequence $(f_n)_{n=1}^\infty$ from [27] with properties (18) and (19). We use this sequence to obtain the sharpness in $L^p$ norms for approximation with piecewise polynomial activation functions as well as with the logistic function.

Theorem 1 in [25] provides a general means to obtain such bounded sequences in Sobolev spaces for which approximation by functions in ${{\mathcal {M}}}_n$ is lower bounded with respect to pseudo-dimension.

We condense sequence $(f_n)_{n=1}^\infty$ to a single counterexample with the next theorem.

Theorem 7

(Sharpness with $L^p$-Norms) Let $\sigma$ be either the logistic function or a piecewise polynomial activation function of type (7) and $r\in \mathbb {N}$. Let $\varOmega$ be the d-dimensional unit ball, $d\in \mathbb {N}$, $1\le p<\infty$. For each abstract modulus of smoothness $\omega$ satisfying (20) and (25), a counterexample $f_{\omega }\in L^p(\varOmega )$ exists such that for $\delta \rightarrow 0+$

$$\begin{aligned} \omega _r(f_{\omega }, \delta )_{p, \varOmega } = {O}\left( \omega (\delta ^{r})\right) \end{aligned}$$

and for $n\rightarrow \infty$

$$\begin{aligned} E({{\mathcal {M}}}_n, f_{\omega })_{p, \varOmega } \ne o\left( \omega \left( \frac{1}{(n [1+\log _2(n)])^{\frac{r}{d}}}\right) \right) . \end{aligned}$$

Proof

We apply Theorem 4 with following parameters for $n\ge 2$:

$$\begin{aligned}&E_n(f):=E({{\mathcal {M}}}_n, f)_{p, \varOmega }, \, X=L^p(\varOmega ),\, S_\delta (f)=\omega _r(f, \delta )_{p, \varOmega },\\&\varphi (x)=\frac{1}{[x(1+\log _2(x))]^\frac{r}{d}}, \quad \mu (\delta )=\delta ^r. \end{aligned}$$

Function $\varphi (x)$ satisfies the prerequisites of Theorem 4 similarly to the proof of Theorem 6. Also, conditions (10)–(13) hold true for $E_n$. For $r\in \mathbb {N}$, we use the sequence $(f_n)_{n=2}^\infty$ of (18) to define resonance elements

$$\begin{aligned} h_n := \frac{1}{\varphi (4n)} \cdot f_{4n} \end{aligned}$$

such that functions $h_n$ are uniformly bounded in $L^p(\varOmega )$ due to (19) in $L^p(\varOmega )$. Thus, (22) is fulfilled. From (18) we obtain resonance condition (24)

$$\begin{aligned} E({{\mathcal {M}}}_{4n}, h_n)_{p, \varOmega }&\ge [4n(1+\log _2(4n))]^\frac{r}{d} \cdot \frac{c}{(4n(\log _2(4n))^{\frac{r}{d}}} \ge c > 0. \end{aligned}$$

Since $(\Vert f_n\Vert _{W_p^{r}(\varOmega )})_{n=2}^\infty$ is bounded, estimate (8) yields (23):

$$\begin{aligned} \omega _r(h_n, \delta )_{p, \varOmega }&= \frac{1}{\varphi (4n)} \omega _r(f_{4n}, \delta )_{p, \varOmega } \le C \frac{\delta ^r}{\varphi (4n)} \le 12^\frac{r}{d} C \frac{\mu (\delta )}{\varphi (n)}. \end{aligned}$$

Thus, all prerequisites of Theorem 4 are fulfilled such that counterexamples exist as stated.$\square$

With respect to error bound (6) for synchronous approximation, counterexamples can be obtained due to the following observation for $\alpha \in \mathbb {N}_0^d$, $|\alpha |=k$:

$$\begin{aligned} \inf&\left\{ \left\| \frac{\partial ^{|\alpha |} (f(\mathbf {x})-g(\mathbf {x}))}{\partial x_1^{\alpha _1}\dots \partial x_d^{\alpha _d}} \right\| _{X^p(\varOmega )}\!\!\!\! : g\in {{\mathcal {M}}}_{n,\sigma }\right\} \ge E\left( {{\mathcal {M}}}_{n,\sigma ^{(k)}}, \frac{\partial ^{|\alpha |} f(\mathbf {x})}{\partial x_1^{\alpha _1}\dots \partial x_d^{\alpha _d}} \right) _{p, \varOmega }. \end{aligned}$$

In the univariate case $d=1$, a counterexample for approximation with $\sigma ^{(k)}$ can be integrated to become a counterexample that shows sharpness of (6). For example, $\sigma (x)=\frac{1}{2}+\frac{1}{\pi } \arctan (x)$ is discussed in [16, Corollary 4.2]. The given proof shows that for each abstract modulus of smoothness $\omega$ satisfying (20) and (25), a continuous counterexample $f_\omega '$ exists such that $\omega _1(f_{\omega }', \delta )_{\infty , \varOmega } = {O}\left( \omega (\delta )\right)$ and $E({{\mathcal {M}}}_{n,\sigma '} f_\omega ')_{\infty , \varOmega } \ne o\left( \omega \left( \frac{1}{n}\right) \right)$. Thus, one can choose $f_\omega (x):=\int _0^x f'_\omega (t)\,dt$. In the multivariate case however, integration with respect to one variable does not lead to sufficient smoothness with regard to other variables.

4 Conclusions

By setting $\omega (\delta ):=\delta ^{\alpha \frac{d}{r}}$, we have shown the following for the logistic function. For each $0<\alpha <\frac{r}{d}$ condition (25) is fulfilled, and according to Theorem 6 there exists a counterexample $f_{\omega }\in C([0, 1]^d)$ with

$$\begin{aligned} \omega _r(f_{\omega }, \delta )_{\infty ,(0, 1)^d} = {O}\left( \delta ^{d \alpha }\right) \quad \text { and }\quad E({{\mathcal {M}}}_n, f_{\omega })_{\infty , (0, 1)^d} =O\left( \frac{1}{n^\alpha }\right) \end{aligned}$$

such that for all $\beta >\alpha$

$$\begin{aligned} E({{\mathcal {M}}}_n, f_{\omega })_{\infty , (0, 1)^d} \ne O\left( \frac{1}{n^\beta }\right) \text { because } \frac{1}{n^\beta } = o\left( \frac{1}{(n[1+\log _2(n)])^\alpha }\right) . \end{aligned}$$

With Theorem 7, similar $L^p$ estimates for the logistic function and $L^2$ estimates for piecewise polynomial activation functions (7) hold true, see direct $L^2$-norm estimate (17). With one input node ($d=1$), a lower estimate for piecewise polynomial activation functions without the $\log$-factor can be proved easily, see [16]. Thus, the bound in Theorem 7 might be improvable.

Future work can deal with sharpness of error bound (6) for synchronous approximation in the multivariate case. By extending quantitative uniform boundedness principles with multiple error functionals (cf. [12, 17, 18]) to non-linear approximation (cf. proof of Theorem 4 in [16]), one might be able to show simultaneous sharpness in different (semi-) norms like this conjecture: Under the preliminaries of Theorem 2, the following might hold true for the logistic activation function: For each abstract modulus of continuity $\omega$ fulfilling (25) there exists a k-times continuously differentiable counterexample $f_\omega$ such that for each $r\in \{0,\ldots ,k\}$ it simultaneously fulfills ($\delta \rightarrow 0+$, $n\rightarrow \infty$)

$$\begin{aligned}&\omega _1\left( \frac{\partial ^{k} f_\omega }{\partial x_1^{\beta _1}\dots \partial x_d^{\beta _d}},\delta \right) _{\infty ,\varOmega } = O\left( \omega \left( \delta \right) \right) \text { for all } \beta \in \mathbb {N}_0^d,\, |\beta | = k,\\&\max _{\alpha \in \mathbb {N}_0^d,\, |\alpha |=r} \inf \left\{ \left\| \frac{\partial ^{|\alpha |} (f_\omega (\mathbf {x})-g(\mathbf {x}))}{\partial x_1^{\alpha _1}\dots \partial x_d^{\alpha _d}} \right\| _{C(\overline{\varOmega })} : g\in {{\mathcal {M}}}_n\right\} \\&\qquad \ne o\left( \frac{1}{(n(1+\log _2(n))^{\frac{k-r}{d}}}\cdot \omega \left( \frac{1}{\root d \of {n(1+\log _2(n))}}\right) \right) . \end{aligned}$$