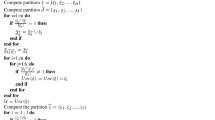1 Introduction

Recent demands of interpretable machine learning [1,2,3,4] opened up new challenges to the research community. Majority of the human experts depend on rules in many classification tasks [5,6,7,8]. Such rule-based classifications are interpretable and highly accurate. Fuzzy systems are usually employed to model a practical problem that is too complex to be described using mathematical models [9, 10]. Acquired knowledge can be understood and readily explained using the IF-THEN fuzzy rules. The fuzzy logic [11] provides a mathematical framework to deal with uncertainty through employing fuzzy rules to represent the knowledge of the model. Fuzzy logic centric methods widely applied in various application such as modeling of heat transfer mechanism [12], energy storage system [13], bio-medical engineering [14], and intelligent system design [15]. Olivas et al. [16] proposed ant colony optimization using type-2 fuzzy, Xiao et al. [17] used fuzzy theory in multi-criteria decision making, Nilashi et al. [18] proposed a fuzzy-based classifier applied in medical images. Fuzzy-based systems also used in many emerging applications such as neural network design [19] and quantum intelligence [20]. There are two important issues in fuzzy system domain; namely: the accuracy (the ability to classify patterns accurately), and the interpretability (the capability to describe the system in an understandable way). These two requirements are usually contradictory to each other [21]. Tuning the fuzzy membership functions of the rules can diminish the modeling error. But the interpretability may also be degraded as the fuzzy sets may drift closer to each other and end up overlapping [22]. Thus, a balance between accuracy and interpretability is desirable.

Rule reduction is one of the research objectives in various rule-based systems. In some analyses, too many useless rules may be a concern in a rule-based system. In this area of researches, data-driven methods [23, 24] are popular but it is data dependent. A Hebbian-based Rule Reduction (HeRR) method has been proposed for this purpose [25]. In the HeRR method, consistent and interpretable rule set is generated through an iterative tuning and reduction process [26].

Although the iterative tuning and reduction process aims to balance the accuracy and interpretability, a good compromise is not always achievable. Furthermore, HeRR may result into a rule set with some amount of redundancy. Further reduction of the rule set is necessary to reduce the model complexity while maintaining high accuracy [24]. It is desirable to modify the previous HeRR system to derive an effective (high accuracy), interpretable (easy to understand) and compact (less redundancy) rule set.

This paper presents a Rough-Set-based Hebbian Rule Reduction (RS-HeRR) system to automatically generate effective, interpretable and compact fuzzy rules for classification problem. In order to maintain the interpretability of HeRR method, the reduction part of the HeRR is performed without any tuning process. To improve the accuracy, a post-processing step is used to polish the generated rule set. This step is implemented using the theory of rough sets. Rough set is a mathematical tool to deal with vague concepts and is domain independent. Hence, it is highly suitable for this problem [27, 28].

Here, we discuss the previously proposed fuzzy systems that exploit the rough set theory [29, 30] and form the basis of RS-HeRR. One of them is the rough-fuzzy multi-layer perceptron (MLP) [31,32,33]. The method successfully applied in robot modeling [34], controlling nonlinear systems [35], and demand prediction [36]. In the rough-fuzzy MLP, the domain knowledge is encoded in the connection weights and rules are generated from the decision table by computing the relative reducts. This model is further pursued using a modular approach in [37, 38]. A multi-class problem is divided into multiple 2-class sub-problems. The rough-fuzzy MLP modules, generated for each class, are subsequently combined to formulate fuzzy rules automatically using genetic algorithm.

Recently developed granulation approach computes granules of fuzzy rules are through rough set approach [39]. While rough sets are used directly in the definition and formation of the fuzzy neural networks, rough sets are not used for direct reduction of rules and attributes. Another rough-fuzzy approach for the identification of fuzzy rules is proposed in [40], which corresponds to tandem approach of hybridization of fuzzy neural networks and rough sets as mentioned in [29]. This types of architectures are also used with support vector machine [41]. The proposed approach is also a tandem approach. The reduction approach of [40] uses the rough set-based attribute reduction algorithms (QuickReduct and QuickReduct II) to reduce the attributes of fuzzy rules derived from the rule induction algorithm (RIA) [42]. This approach attempts to compute a minimal reduct without exhaustively generating all possible subsets of attributes. However, it does not guarantee to always generate a minimal reduct. Further improvement for this approach is proposed in [40]. It uses the fuzzy-rough set [43] to provide better guidance in the selection of attributes. A hybrid of fuzzy neural network and the rough set, called rough sets-based outer-product (RSPOP), has been proposed in [44, 45] and extended in [46]. The RSPOP algorithm utilizes the rough set theory to perform the reduction of the attributes of the fuzzy rules generated by the pseudo outer-product (POP) rule identification algorithm [47, 48]. It uses the accuracy which is derived using subsets of attributes, to guide the computation of the relative reduct. We note that attribute reduction of RS-HeRR can be incorporated into RF-MLP and granulation approaches for applications such as medical image segmentation problems [49, 50].

The main contributions of the paper are as follows:

  1. 1.

    We have proposed a generalized rule generation and reduction method, namely RS-HeRR. The method produce state-of-the-art results in four variety of classification tasks without compromising accuracy.

  2. 2.

    Motivated by the existing methods, RS-HeRR performs optimization of accuracy, interpretability, and compactness of rule set using a rough-set-based attribute set selection approach using partial dependency.

The main novelty of our method is that we pay attention to the interpretability of learning methods. We have introduced an automatic rule generation and reduction module to build a compact learning framework. The method utilizes a combination of fuzzy logic and rough-set to achieve the goal. We made a theoretical foundation of the proposed method and also applied on four public classification dataset. The results conclude that the method is generic and can be applied to different classification tasks.

This paper is organized as follows. Section 2 describes a summary of the Hebbian-based Rule Reduction (HeRR) algorithm and Sect. 3 present the proposed Rough-Set-based Hebbian Rule Reduction (RS-HeRR) system. Four sets of experimental results are presented in Sect. 4 to benchmark and demonstrate the effectiveness of the proposed method; Sect. 5 presents the conclusion.

2 Hebbian-based rule reduction system

Fuzzy models usually consist of four components, a fuzzifier, a rule base, an inference engine and a defuzzifier. Crisp inputs are fuzzified to fuzzy inputs through a fuzzifier. Fuzzy inference is performed in the inference engine based on a set of fuzzy rules, as shown in Fig. 1.

Fig. 1
figure 1

Fuzzy rule (Mamdani type)

Full size image

It transforms the fuzzy inputs to the fuzzy outputs. These fuzzy outputs are defuzzified to the crisp outputs through a defuzzifier. The crisp input and output vectors are represented as \(\mathbf {X^T}=[x_1,x_2,\ldots ,x_i,\ldots ,x_{n1}]\), \(\mathbf {Y^T}=[y_1,y_2,\ldots ,y_i,\ldots ,y_{n5}]\), where n1 and n5 are the input and output dimensions, respectively [3]. Gaussian membership functions (MF) are used for fuzzification and defuzzification in this paper. Although other types of membership functions such as triangular, trapezoidal, etc. can also be used in our case. We have used Gaussian MF because of its advantage of being smooth and nonzero at all points. The centroids and widths of the MFs are variables in the framework and denoted as \((c_{i,j}^{in},\delta _{i,j}^{in})\), the i-th input dimension and the j-th MF, and \((c_{l,m}^{\mathrm{out}},\delta _{l,m}^{\mathrm{out}})\), the l-th output dimension and the m-th MF, for the input and output counterparts of the rules, respectively. Denote \(i{L_k}(i)\) as the input label in the i-th input dimension of the k-th rule, and as the output label in the m-th output dimension of the k-th rule. Although the framework of Fig. 1 is valid for multi-input-multi-output (MIMO) systems, we consider only classification problems which are multi-input-single-output (MISO). The centroids of the single output are denoted as \(c_l^\mathrm{out}\) (l-th MF), and the widths of the output MF are not involved in the computation. The output label of the k-th rule is represented as \(oL_k\). The minimum and the maximum functions are used for fuzzy union and intersection operators, respectively. Given the input vector \(\mathbf {X^T}=[x_1,x_2,\ldots ,x_i,\ldots ,x_{n1}]\), the output of the fuzzy system can be expressed as Eq. (1), where \(f_k\) is called the firing strength of the input point \(\mathbf {X^T}\) by the k-th rule and define in Eq. (2).

$$\begin{aligned} o &= c_{k'}^{\mathrm{out}}, k' = \mathop {\arg \max }\limits _k (f_k) \end{aligned}$$
(1)
$$\begin{aligned} f_k &= \mathop {\min }\limits _i \bigg ( \exp \big ( \frac{( x_i - c_{i,i{L_k}(i)}^{in})^2}{({{\delta _{i,i{L_k}(i)}^{in}} )}^2}\big )\bigg ) \end{aligned}$$
(2)

Hebbian-based rule reduction neuro-fuzzy system [25] consists of 4 steps shown in Fig. 2, namely initial rule set generation, rule ranking, membership functions merging, and redundancy removal. We discuss each step in detail as this framework is used directly by RS-HeRR.

Fig. 2
figure 2

The four procedures of the Hebbian-based rule reduction neuro-fuzzy system

Full size image

The initial rule set is generated from the training data samples. If there are no rules in the rule base or no rules with sufficient firing strength (threshold \(\theta \)), a new rule node is created. When a new rule is created, the centroids of the newly generated MFs for the input dimensions are assigned the value of the current data sample, while the widths of the MFs are set to a predefined value in proportion to the scale of each dimension. The centroid of the output dimension is assigned a value equal to the class label. The flowchart of the procedure is described in Fig. 3.

Fig. 3
figure 3

Flowchart of rule initialization algorithm

Full size image

In the next step, all the initial rules are ranked and sorted based on their Hebbian importance. In fuzzy modeling, each fuzzy rule corresponds to a sub-region of the decision space. Some rules lying in an appropriate region may represent many samples and have much influence on the final result, while some other rules may occasionally be generated by noise and become redundant in the rule base. As the membership functions of a rule are determined, the training sample \((\mathbf {X^T},y_i)\) is fed into both the condition and consequence parts of the rule simultaneously. The input \(\mathbf {X^T}\) is used to determine the firing strength of the rule. If the class label of the rule (the centroid of the consequence part) is the same as \(y_i\), it is given a membership of 1. Otherwise, the membership is assigned 0. If the input-output samples repeatedly fire a rule by the product of their firing strength and the membership values of consequence part, such that the accumulated strength surpasses that of other rules, it indicates the existence of such a rule. The larger the product is, the more important the rule is deemed. The Hebbian importance of the k-th rule is defined in Eq. (3).

$$\begin{aligned} I_k = \sum \limits _{i = 1}^n {{f_{k,i}}} \times {\mu _{o{L_k}}}( {{y_i}} ) \end{aligned}$$
(3)

where \(f_{k,i}\) is the firing strength of the k-th rule on the i-th data point and

$$\begin{aligned} o{L_k}(y_i)={\left\{ \begin{array}{ll} 0 &{} \text {if }c_k^{\mathrm{out}} \ne {y_i} \\ 1 &{} \text {if }c_k^{\mathrm{out}} = {y_i}. \end{array}\right. } \end{aligned}$$

The fuzzy rules are sorted in a decreasing order of \(I_k\). This is called the Hebbian ordering of the rules.

The next step is merging of membership functions and rules reduction by redundancy and inconsistency removal, which are performed iteratively. Their flowchart is shown in Fig. 4. In the beginning of this flowchart, Hebbian ordered rules are contained in the original rule set R and the initial reduced rule set \(R'\) is null. If there is no rule in the reduced rule set, the rule with highest Hebbian importance in R is added into \(R'\), otherwise, the fuzzy set in each dimension of the rule is added or merged into the fuzzy sets in \(R'\) according to a set of criteria defined below. All the newly added or merged fuzzy sets are linked together to formulate a new rule in the reduced rule set \(R'\).

Fig. 4
figure 4

Flowchart of merging of membership functions and rule reduction algorithm

Full size image

Since some fuzzy sets may be shared by several rules, changing a fuzzy set is equivalent to modifying these rules simultaneously. Thus, to merge the MFs, the fuzzy set associated with each MF is assigned an importance value which is equal to the sum of importance of the rules which share the fuzzy set. Let us denote the importance value of a fuzzy set F as \(\hat{I_F}\). The value of \(\hat{I_F}\) changes during the merging process. Each time the k-th rule (i.e., the k-th rule is “If \(x_i = A_i\) then \(y_1 = C_k\)”) in the original rule set R is presented, its fuzzy sets \(A_i (i = 1 \ldots {n_1})\) in the condition part, would have the same importance with the Hebbian importance of the associated rule and is described in Eq. (4).

$$\begin{aligned} \hat{I}_{A_i} = I_k ( i = 1 \ldots {n_1}) \end{aligned}$$
(4)

As the consequence part of a rule is the class label, \(C_1\) does not participate in the merging process. In each input dimension i, among the fuzzy sets in the reduced rule set \(R'\) of this dimension, the fuzzy set \(A'_i\) with the maximum degree of overlap over \(A_i\) (the degree of overlap is defined in Eq. (8)) is selected. If the maximum degree of overlap satisfies a specified criterion, they are merged into another fuzzy set \(A''_i\), otherwise, the fuzzy set \(A_i\) is directly added into the reduced rule set of this dimension. The centroid and the width of \(A_i\) and \(A'_i\); namely: \((c_{A_i},\delta _{A_i})\) and \((c_{{A'}_i},\delta _{{A'}_i})\), respectively, are merged into \(({c_{A''}}_i,\delta _{{A''}_i})\) using Eqs. (5) and (6).

$$\begin{aligned} c_{{A''}_i} = \frac{\hat{I}_{A_i}{c_{{A_i}} + {{\hat{I}}_{{{A'}_i}}} {c_{{{A'}_i}}}}}{{{{\hat{I}}_{{A_i}}} + {{\hat{I}}_{{{A'}_i}}}}} \end{aligned}$$
(5)

M2:

$$\begin{aligned} {\delta _{{{A''}_i}}} = \frac{{{{\hat{I}}_{{A_i}}}{\delta _{{A_i}}} + {{\hat{I}}_{{{A'}_i}}}{\delta _{{{A'}_i}}}}}{{{{\hat{I}}_{{A_i}}} + {{\hat{I}}_{{{A'}_i}}}}} \end{aligned}$$
(6)

The importance of the new fuzzy set \({A''_i}\) is determined using Eq. (7).

M3:

$$\begin{aligned} {\hat{I}_{{{A''}_i}}} = {\hat{I}_{{A_i}}} + {\hat{I}_{{{A'}_i}}} \end{aligned}$$
(7)

In other words, the centroid and variance of the resultant fuzzy set is the weighted average of the two fuzzy sets in accordance with their importance, and the degree of importance of this final fuzzy set is the sum of the importance of the two. Subsequently the newly generated fuzzy set \({A''_i}\) replaces the previous fuzzy set \({A'_i}\). Finally, the newly added or merged fuzzy sets in all the dimensions are linked together to form a fuzzy rule in the reduced rule set \(R'\). Given fuzzy sets A and B, the degree of overlap of A by B is defined as in Eq. (8).

$$\begin{aligned} {S_A}( B ) = \bigg | {\frac{{A \cap B}}{A}} \bigg | \end{aligned}$$
(8)

As the Gaussian membership function is used in the proposed method, the overlap measure can be derived using the centroids and widths of the MFs. For fuzzy sets A and B, with membership functions given in Eqs. (9), (10), respectively, where \({c_A}\) and \({c_B}\) are their centroids, \(\delta _A\) and \(\delta _B\) are their widths; and assuming that \(c_A \ge c_B\), then |A| and \(\left| {A \cap B} \right| \) can be expressed in Eqs. (11) and (12).

$$\begin{aligned} {\mu _A}( x ) &= \exp \bigg \{ \frac{- {(x - c_A)}^2}{\delta _A^2}\bigg \} \end{aligned}$$
(9)
$$\begin{aligned} {\mu _B}( x ) &= \exp \bigg \{ \frac{- {(x - c_B)}^2}{\delta _B^2}\bigg \} \end{aligned}$$
(10)
$$\begin{aligned} | A| &= \sqrt{\pi }{\delta _A} \end{aligned}$$
(11)
$$\begin{aligned} | {A \cap B}| &= \frac{1}{2}\left( \frac{{{h^2}\left[ {{c_B} - {c_A} + \sqrt{\pi }\left( {{\delta _A} + {\delta _B}} \right) } \right] }}{{\sqrt{\pi }\left( {{\delta _A} + {\delta _B}} \right) }} \right. \\&\qquad + \frac{{{h^2}\left[ {{c_B} - {c_A} + \sqrt{\pi }\left( {{\delta _A} - {\delta _B}} \right) } \right] }}{{\sqrt{\pi }\left( {{\delta _B} - {\delta _A}} \right) }} \\&\qquad \left. + \frac{{{h^2}\left[ {{c_B} - {c_A} - \sqrt{\pi }\left( {{\delta _A} - {\delta _B}} \right) } \right] }}{{\sqrt{\pi }\left( {{\delta _A} - {\delta _B}} \right) }} \right) \end{aligned}$$
(12)

where \(h(x) = \max \left\{ {0,x} \right\} \). The criterion of merging is as follows, if \({S_A}\left( B \right) > \lambda \) or \({S_B}\left( A \right) > \lambda \), the two fuzzy sets A and B are merged, where \(\lambda \) is a specified threshold that determines the maximum degree of overlap between fuzzy sets that the system can tolerate. Higher \(\lambda \) may increase the accuracy but degrade the interpretability, while lower \(\lambda \) may force a larger number of rules to be reduced but at the risk of the number of rules being less than necessary to maintain the required modeling accuracy. In the algorithm, the current rule set R consists of the fuzzy rules derived from the rule initialization algorithm and the reduced rule set \(R'\) is the resultant rule set and is set to null at the beginning. There are two loops in the flowchart, where the outer loop is for each fuzzy rule \({r_i}\) and the inner loop is for each input dimension j. If some fuzzy set of the dimension j in the \(R'\) is very similar to the fuzzy set of dimension j of the rule \({r_i}\) (i.e., the similarity measure S is larger than a predefined value), these two fuzzy sets are merged into a new fuzzy set according to Eqs. (5) and (6). Otherwise, the fuzzy set of dimension j of the rule \({r_i}\) are added into the reduced rule set \(R'\). All the newly merged or added fuzzy sets are linked together and inserted into \(R'\). The last step is the redundancy and inconsistency removal. After the merging process, the reduced rule set \(R'\) consists of a set of modified rules. The following three steps are used to remove redundancy in \(R'\):

  1. 1.

    If there is only one membership function within one dimension, this dimension (feature) is removed;

  2. 2.

    If there is any rule that has the same conditions and consequences with the others, it is removed;

  3. 3.

    If there are any conflicting rules that have equivalent conditions but different consequences, the one with the higher degree of importance is preserved and the others are deleted.

3 RS-HeRR: the hybrid of Hebbian-based rule reduction system and rough set

Although the Hebbian rule reduction method is proposed to remove redundant rules and attributes through the merging process, redundancy may still remain. For example, if a conditional attribute, which is unrelated with the decision attribute, cannot be merged into a membership function, this conditional attribute will become redundant for the rule set. Thus, further reduction of the generated rule set is desirable. This is the goal of RS-HeRR. Rule set is initially generated through the Hebbian rule reduction algorithm and the rough set theory is used as a post-processing step to further reduce the generated rule set without affecting the classification accuracy.

As discussed in the introduction, the proposed RS-HeRR uses both the partial dependency (used in QuickReduct algorithms [40]) and the system’s performance (used in RSPOP [44, 45]) to select attributes and reduce fuzzy rules. QuickReduct algorithms aim to find the ‘reduct’ of the rough set through rule selection based on partial dependency. We describe the concept of dependency, and partial dependency below.

In the theory of rough sets, a knowledge base can be represented as a relational system \(K = \left( {{\mathbf{U}},{\mathbf{R}}} \right) \), where \({\mathbf{U}} \ne \emptyset \), called the universe, is a set of objects, and \({\mathbf{R}}\) is a set of relations. In the knowledge base, \({\mathbf{R}}\) particularly consists of a set of attributes, each of which forms an equivalence relation. For any \({\mathbf{P}} \subseteq {\mathbf{R}}\), an associated equivalence relation, called indiscernibility relation over P, denoted by \(IND\left( {\mathbf{P}} \right) \), is formed in Eq. (13):

$$\begin{aligned} IND\left( {\mathbf{P}} \right) = \bigg \{ {\left( {x,y} \right) \in {U^2}|\forall a \in {\mathbf{P}},a(x) = a(y)} \bigg \} \end{aligned}$$
(13)

The family of all equivalence classes of the equivalence relation \(IND\left( {\mathbf{P}} \right) \) is denoted by \({\mathbf{U}}/{IND\left( {\mathbf{P}} \right) }\). With each subset \(X \subseteq U\) and an equivalence relation R, the rough set theory uses the R-lower \((\underline{R} X)\) and R-upper \((\overline{R} X)\) approximations to approximate X, as described in Eqs. (14) and (15).

$$\begin{aligned} \underline{R} X &= \cup \left\{ {Y \in {{\mathbf{U}} /R}|Y \subseteq X} \right\} \end{aligned}$$
(14)
$$\begin{aligned} \overline{R} X &= \cup \left\{ {Y \in {{\mathbf{U}} / R}|Y \cap X \ne \emptyset } \right\} \end{aligned}$$
(15)

By employing the knowledge R, \(\underline{R} X\) is the set of all objects of \({\mathbf{U}}\) which can be classified with certainty as the elements of X, and \(\overline{R} X\) is the set of objects of \({\mathbf{U}}\) which can be possibly classified as elements of X. Let P and Q be two equivalence relations in \({\mathbf{U}}\), the positive, negative and boundary regions are defined by Eqs. (16)–(18):

$$\begin{aligned} PO{S_P}\left( Q \right) = \mathop \cup \limits _{X \in {{\mathbf{U}}/ Q}} \underline{P} X \end{aligned}$$
(16)
$$\begin{aligned} NE{G_P}\left( Q \right) = {\mathbf{U}} - \mathop \cup \limits _{X \in {{\mathbf{U}} / Q}} \overline{P} X \end{aligned}$$
(17)
$$\begin{aligned} BN{D_P}\left( Q \right) = \mathop \cup \limits _{X \in {{\mathbf{U}} / Q}} \overline{P} X - \mathop \cup \limits _{X \in {{\mathbf{U}} / Q}} \underline{P} X \end{aligned}$$
(18)

For a knowledge base, dependency between attributes may exist. Let \({\mathbf{P}},{\mathbf{Q}} \subseteq {\mathbf{R}}\). \({\mathbf{Q}}\) depends on \({\mathbf{P}}\) if \(IND\left( {\mathbf{P}} \right) \subseteq IND\left( {\mathbf{Q}} \right) \). The dependency can also be partial which means that only part of \({\mathbf{Q}}\) depends on \({\mathbf{P}}\). For a partial dependency, \({\mathbf{Q}}\) depends on \({\mathbf{P}}\) in a degree \({\gamma _{\mathbf{P}}}\left( {\mathbf{Q}} \right) \) \(\left( {0 \le {\gamma _{\mathbf{P}}}\left( {\mathbf{Q}} \right) \le 1} \right) \), described in Eq. (19).

$$\begin{aligned} {\gamma _{\mathbf{P}}}\left( {\mathbf{Q}} \right) = \frac{{{{\textit{card }}}\,PO{S_{\mathbf{P}}}\left( {\mathbf{Q}} \right) }}{{{{\textit{card } }}{\mathbf{U}}}} \end{aligned}$$
(19)

Where card() is the cardinality of the input set, i.e., \({{\textit{card }}}\,PO{S_{\mathbf{P}}}\left( {\mathbf{Q}} \right) \) and \({{\textit{card }}}{\mathbf{U}}\) denote the number of elements in \(PO{S_{\mathbf{P}}}\left( {\mathbf{Q}} \right) \) and \({\mathbf{U}}\), respectively.

Fig. 5
figure 5

The hybrid of the Hebbian rule reduction fuzzy system and the rough set

Full size image

A simple depiction of RS-HeRR is given in Fig. 5. Initially, when training samples are available, a rule set is generated by the Hebbian rule reduction method. Then, using this set of rules (denoted as \(RuleSet\left( {A,C} \right) \)), the accuracy due to each attribute is also computed. Similar to QuickReduct, an additive approach is used for building the new rule set, however, guided primarily by the classification accuracy. This implies that the new attribute set R is initially empty. The attribute which single handedly gives the best classification accuracy is the attribute first transferred to R. It is investigated if the accuracy of R is poorer than the accuracy of \(RuleSet\left( {A,C} \right) \). For each remaining attribute \(\left\{ a \right\} \), the classification accuracy of \(R \cup \left\{ a \right\} \) is computed. The attribute, whose inclusion gives the best accuracy is included in R. In the case of a tie for best accuracy, partial dependency \({\gamma _{R \cup \left\{ a \right\} }}\left( C \right) \) and \({\gamma _R}\left( C \right) \) is computed for the attributes resulting into the tie. The attribute with maximum partial dependency is added to R. If there is a situation of tie in the partial dependency as well, one of them is randomly chosen. The algorithm terminates when the partial dependency becomes one and the classification rate using the subset of attributes is not worse than that using the whole set of the attributes. Conceptually, it implies that RS-HeRR tackles the conditional attribute for redundancy handling which is uncorrelated with the decision attributes (i.e., contributors to accuracy). The pseudo-code of the attribute selection algorithm is presented in Algorithm 1. We also present an example in Sect. 4.1 to explain the procedure.

figure a

4 Experimental results

In this section, we use four binary classification problems and demonstrate the effectiveness of RS-HeRR in meeting the three requirements, namely classification performance, interpretability, and compactness. The datasets of the classification problems are detailed in individual sub-sections but a brief summary is provided in Table 1. The amount of cross-folding validation (CV) used and the ratio of number of training data samples (#Train) to the number of test data samples (#Test) is given in Table 1. Notably, we use smaller subset for training as compared to the test subset. The purpose of using the smaller subset of data as the training set is to test and compare the generalization ability of the proposed system and other benchmarked models.

Table 1 The details of the datasets and the associated binary classification problem
Full size table

Classification performance is quantitatively assessed using overall classification accuracy over both classes, specificity for the positive class, and sensitivity for the negative class. For binary classification problem, the sensitivity is the accuracy for the positive class, and the specificity is the accuracy for the negative class. They are computed using Eqs. (20) and (21), respectively.

$$\begin{aligned}&{\mathrm{Sensitivity }}= \frac{{{{\text {Number of positive samples correctly predicted}}}}}{{{{\text {Total number of positive samples}}}}} \end{aligned}$$
(20)
$$\begin{aligned}&{\mathrm{Specificity }}= \frac{{{{\text {Number of negative samples correctly predicted}}}}}{{{{\text {Total number of negative samples}}}}} \end{aligned}$$
(21)

We compare the classification performance of the RS-HeRR with Support Vector Machine (SVM) [51], the C4.5 decision tree algorithm [52], the Naïve Bayesian classifier (NB) [53], and the Rough-Set-based Pseudo Outer-Product fuzzy rule identification algorithm (RSPOP) [45]. Our selection of these methods for comparison is explained as follows. For comparison of accuracy, we consider the classification methods that concern with different formats of knowledge representation and concern with achieving accuracy rather than factors such as interpretability or compactness. Our selection was also guided by the availability of the codes or executables of the methods being compared.

Interpretability is measured by the number of fuzzy rules used for representing the knowledge. For other factors concerning interpretability remaining the same, such as the type of membership functions, the architecture, etc., the interpretability due to the attribute selection strategy is better if the number of rules after selection is less than the number of rules obtained using other attribute selection strategies. Similarly, compactness of the fuzzy system is characterized by the number of attributes as well as the number of rules. Here also, a fair comparison requires that other factors of the fuzzy system are kept the same and the compactness due to the attribute selection strategies is compared. Thus, for analyzing the advantage of RS-HeRR regarding interpretability and compactness, we use same initial fuzzy systems as obtained using the basic HeRR strategy explained in Sect. 2 and compare RS-HeRR with the cases where no attribute is used (original HeRR) or QuickReduct and QuickReduct II are used for attribute selection. We refer to this comparison as attribute selection comparison.

4.1 Pima indian diabetes dataset

The Pima-Indian Diabetes dataset [54] consists of a total of 768 data instances, all of which are for the patients who are female of at least 21 years old Pima Indian heritage. There are 8 input features for each instance, listed in Table 2. Figure 6 shows the benchmark results of the RS-HeRR against the SVM, C4.5, NB, and RSPOP. The RS-HeRR system achieve the highest overall testing accuracy, though its sensitivity is lower than that of SVM by only 4.36 and its specificity is worse than that of C4.5 and NB by less than 4.37%. This poor performance is attributed to the use of Mamdani model of fuzzification, which favors interpretability over accuracy.

Table 2 The description of the eight features of the Pima Indian diabetes dataset
Full size table
Fig. 6
figure 6

Classification results on the Pima Indian diabetes dataset (statistics over 10 cross-fold validation)

Full size image
Table 3 Results on the Pima Indian diabetes dataset, compared with the QuickReduct, QuickReduct II and without rough set reduction (statistics over 10 cross-fold validation)
Full size table
Table 4 The training accuracy and partial dependency using \(x_1\) to \(x_8\)
Full size table
Table 5 The training accuracy and partial dependency using \(x_1,x_3,x_4,x_5,x_6,x_7,x_8\)
Full size table
Table 6 The training accuracy and partial dependency using \(x_1,x_3,x_4,x_5,x_7,x_8\)
Full size table

The results for attribute selection comparison are shown in Table 3. The overall accuracy, the number of generated rules and the number of selected features are given in the table for comparison. The classification accuracy of the HeRR without rough set is the worst among these models, and the number of rules and features are much higher than others. It indicates that the redundancy in the rule set could have degraded the testing accuracy of the HeRR system and the removal of redundant rules and features is necessary to maintain and boost the performance. The RS-HeRR system achieves a decrease of 58.37% for the number of rules and 60.76% for the number of features, compared with the HeRR system without any feature selection process. The decrease is larger than the HeRR system plus QuickReduct and QuickReduct II. It indicates the rule set derived by RS-HeRR is more compact than that derived by HeRR plus QuickReduct & QuickReduct II. The experimental results thus show the superior performance of the proposed rough-set-based attribute selection.

After the Hebbian rule reduction algorithm shown in Fig. 2, a total of 17 fuzzy rules are derived. The classification accuracy on the training and testing sets are 80.52% and 71.35%, respectively. At the beginning of RS-HeRR, the attribute set A consists of all the attributes \({x_1} - {x_8}\), and the output attribute set R is empty. For each attribute a in \(A - R\), the training accuracy and the partial dependency using the rule set with the attribute set \(R \cup \{ a\}\) are shown in Table 4. It is seen that when the attribute \({x_2}\) is added to R, the training classification achieved the maximum among all the 8 attributes. Thus, R becomes \(\{ {x_2}\}\). As the training accuracy is worse than that using the whole attribute set, the selection process continues. In the second round of the loop, the training accuracy and partial dependency of the remaining 7 attributes are shown in Table 5. In the table, both \({x_6}\) and \({x_8}\) achieves the best in training accuracy. However, the partial dependency of \({x_6}\) is larger than that of \({x_8}\). Thus, the attribute \({x_6}\) is selected. As the training accuracy is still lower than 80.52%, which is achieved by the whole attribute set, the algorithm comes into the third round. The training accuracy and partial dependency are shown in Table 6. The best accuracy is achieved by adding \({x_7}\) to R. Hence, \({x_7}\) is selected. As the accuracy is not lower than 80.52% and the partial dependency becomes 1, the algorithm terminates. At the end of the algorithm, the attribute set \(\{ {x_2},{x_6},{x_7}\}\) is produced. Using the 3 attributes, the rule set is simplified into 6 rules by deleting repeated rules. The training accuracy is still maintained at 80.52%. However, the testing accuracy is boosted to 75.40%, which is better than before, due to the selection of the attributes.

The interpretability of the proposed RS-HeRR system is evaluated in Figs. 7, 8, 9 and Table 7. Figures show the membership functions of the attributes: \({x_2},{x_6}\) and \({x_7}\). \({x_2}\) is divided into 2 MFs (Low and High), and \({x_6}\) and \({x_7}\) are divided into 3 MFs (Low, Medium and High). It is shown that the divided MFs are all clearly separated and have distinguished semantic meanings. The resultant rule set which consists of a total of 6 fuzzy rules is shown in Table 8. From the rule set, it can be seen that, when the \({x_2}\) (Plasma glucose concentration) is low and the \({x_6}\) (Body mass index) and \({x_7}\) (Diabetes pedigree function) are not high, the patient will be tested as positive for diabetes, and when \({x_2}\) (Plasma glucose concentration) is high and the \({x_6}\) (Body mass index) is not low, the patient will be tested as negative for diabetes. The derived rule set can be easily understood by humans and used to assist the decision making of the clinicians.

Fig. 7
figure 7

Derived fuzzy membership functions of attribute \(x_2\)

Full size image
Fig. 8
figure 8

Derived fuzzy membership functions of attribute \(x_6\)

Full size image
Fig. 9
figure 9

Derived fuzzy membership functions of attribute \(x_7\)

Full size image
Table 7 The six derived fuzzy rules
Full size table

4.1.1 Urban water treatment plant monitoring dataset

The urban water treatment datasetFootnote 1 consists of a set of historical data measured from an urban waste water treatment plant over a period of 527 days. The objective is to classify the operational state of the plant in order to predict faults through the state variables of the plant at each of the stages in the treatment process. In total, 38 input features for each data point, organized into 5 aspects, are used (see Table 8).

Table 8 The five aspects of the input features
Full size table
Table 9 The 13 statuses of the water treatment plant
Full size table

The status of the plant is represented by one of 13 different categories. Some represent the normal operation of the plant and others point out various faults of the plant. They are listed in Table 9. As all the faults appear in a short period and are dealt with immediately, there are not enough training data points for these categories. However, for the statuses normal function (green shaded row in Table 9) and abnormal event (blue shaded row in Table 9), there are 513 and 14 data samples, respectively. Even after clustering statuses corresponding to normal and abnormal performance, the dataset is a highly skewed dataset and thus it is difficult to obtain good specificity (accuracy for abnormal samples). Further, there are missing values for some features in this dataset. The missing values are replaced by the average value of the corresponding attribute in this experiment. This substitution may be considered as noise in the data samples.

The classification results are shown in Fig. 10. RSPOP achieves a sensitivity of 100%, classifying all the positive samples correctly across all the CV groups. However its performance in classifying negative samples is bad, as its specificity is lower than others. In this experiment, RS-HeRR achieves the best specificity. It shows that the RS-HeRR system outperforms other models in overall testing accuracy, although its sensitivity is slightly lower than that of SVM, C4.5 and RSPOP. This is attributed to the property of RS-HeRR in favoring accuracy even while identifying the critically important attributes through partial dependency. The experimental results show the classification capability of the RS-HeRR in the dataset where the classes are unbalanced distributed.

Fig. 10
figure 10

Classification results on the urban water treatment dataset (statistics over 10 cross-fold validation)

Full size image
Table 10 Classification results on the urban water treatment dataset, compared with the QuickReduct, QuickReduct II and without rough set reduction (statistics over 10 cross-fold validation)
Full size table

Table 10 shows the attribute selection comparison results. The testing accuracy achieved by RS-HeRR is the same as that of HeRR without RS, while the HeRR plus QuickReduct and QuickReduct II achieve lower accuracy. Under the percentage decrease in the number of rules and features, compared with the HeRR without RS, the proposed RS-HeRR outperforms the HeRR with QuickReduct & QuickReduct II. We note that in some cross-validation sets, RS-HeRR, HeRR + QuickReduct, and HeRR + QuickReductII, all select only one feature. But, the selected feature in RS-HeRR is the one that provides the best accuracy rather than maximum partial dependency. This is critical since such set of CV may have only one or two negative samples. It indicates that the RS-HeRR derives a more compact rule set while still maintaining the accuracy.

4.2 Sonar dataset

The Sonar dataset [55] consists of a total 208 pattern samples with 60 input features and two classes (metal target and rock target). Figure 11 shows the classification results of RS-HeRR, compared with SVM, C4.5, NB, and RSPOP. The proposed RS-HeRR system yields an accuracy of \(89.41\pm 1.75\)%. The standard deviation of both the accuracy and sensitivity is lower than that of other models. In shows that classification capability of the proposed RS-HeRR is better than the others in this dataset.

The attribute selection comparison results are given in Table 10. The HeRR without the RS attribute selection yields the highest testing accuracy, while the performance of the proposed RS-HeRR is at the second place. Notably, Table 11 shows that the HeRR system will involve all the 60 input features in the classification if no attribute selection process is incorporated. Such system is difficult to interpret. RS-HeRR only involves \(11 \pm 4.58\)% input features, at a cost of about 1% degradation in accuracy. The results show that, a balance between accuracy and interpretability is achieved by the proposed RS-HeRR. The HeRR with QuickReduct competes well with RS-HeRR. Although its accuracy is slightly lower than that of RS-HeRR, the number of both derived rules and selected features is less than that of RS-HeRR. This is because RS-HeRR prioritizes accuracy over partial dependency and the accuracy may inherently be poor in noisy measurements, such as in the case of sonars which have poor signal to noise ratio in the presence of cluttered background. The HeRR with QuickReduct II derives the least number of rules, but its accuracy is much lower than others.

Fig. 11
figure 11

Classification results on the sonar dataset (statistics over 10 cross-fold validation)

Full size image
Table 11 Classification results on the sonar dataset, compared with the QuickReduct, QuickReduct II and without rough set reduction (statistics over 10 cross-fold validation)
Full size table

4.3 Ovarian cancer dataset

The ovarian cancer DNA microarray gene expression dataset [56] consists of a total of 54 patterns where 30 examples are derived from ovarian tumors and 24 examples are normal. Each of these examples comprises 1536 features. This is a good example of a highly complex and uninterpretable problem where attribute reduction and compact rule base is highly desirable.

In Fig. 12, the RS-HeRR yields an accuracy of \(96.30 \pm 3.21\)%. The SVM, C4.5 and NB yield the same average accuracy, 90.74%, where the standard deviation of the accuracy of C4.5 and NB is the same. Table 12 shows attribute selection comparison results. RS-HeRR selects only \(2.67\pm 0.58\) features out of the whole 1536 features for classification. This indicates the ability to represent the knowledge using about only three attributes (which corresponds to only 3 genes) and about only 12 rules (12 genetic combinations characterizing the presence or absence of ovarian cancer). However, the accuracy is enhanced from \(70.37 \pm 6.41\) to \(96.30 \pm 3.21\). This is because of the elimination of the attributes that affect classification accuracy adversely. The performance of the RS-HeRR and HeRR with QuickReduct in the terms of testing accuracy is the same. However, the RS-HeRR selects and derives less number of features and less number of rules than that of HeRR with QuickReduct. The proposed attribute selection algorithm outperforms the QuickReduct, as the proposed algorithm makes the rule set more compact.

Fig. 12
figure 12

Classification results on the ovarian cancer dataset (statistics over 3 cross-fold validation)

Full size image
Table 12 Classification results on the ovarian cancer dataset, compared with the QuickReduct, QuickReduct II and without rough set reduction (statistics over 3 cross-fold validation)
Full size table

5 Conclusion

This paper proposes RS-HeRR, the hybridization of Hebbian rule reduction fuzzy system and rough set theory, for generating fuzzy rules for pattern classification problems. The rule set is initially generated using the Hebbian-based rule reduction algorithm. A post-processing step is used to further remove redundant attributes based on the rough set theory. In this step, a rough-set-based attribute selection algorithm is proposed to reduce and simplify the rule set without affecting the classification accuracy. It uses both the system’s performance and partial dependency as guides to determine suitable attributes subset. The key strengths of the proposed methods are summarized as follows:

  1. 1.

    Compact, effective and interpretable rule set: a compact, effective and interpretable rule set is generated from the trained fuzzy system. The redundancy is removed from the rule set using rough-set-based attribute selection algorithm, while the classification performance is maintained and boosted. Membership functions in each dimension are clearly separated and the size of the resultant rule set is small. It makes the rule set readily understandable by human.

  2. 2.

    No additional control parameter: HeRR needs only two control parameters, namely initial rule set generation threshold \(\theta \) and the membership function merge threshold \(\lambda \) (see Sect. 2). RS-HeRR does not require any additional parameter.

The performance of the proposed rough-set-based Hebbian rule reduction system is evaluated using four datasets: (1) the Pima Indian diabetes dataset; (1) the urban water treatment plant monitoring dataset; (3) the sonar dataset; (4) the ovarian cancer dataset. The experimental results show good performance by the proposed method, when benchmarked against with other well established classifiers. In certain challenging classification problems, such as skewed dataset of the urban water treatment plant monitoring characterized with very few negative sample and the ovarian cancer dataset characterized by huge number of features, RS-HeRR shows a huge advantage. For instance, RS-HeRR can reduce the knowledge from the data characterized by 1536 features in the ovarian cancer dataset to identification of 3 genes and 12–14 genetic combinations that characterize the presence of ovarian cancer.

There are a few future avenues of the proposed method. First, we will apply a similar mechanism in the image classification domain. Next, we will consider extending the method with a combination of deep neural networks. This may open up new possibilities and challenges in the domain of interpretable and explainable artificial intelligence.