On the secrecy outage probability and performance trade-off of the multi-hop cognitive relay networks

Abstract

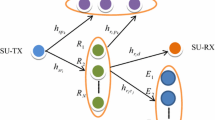
We study the physical-layer security of multi-hop secondary network under spectrum sharing constraint caused by the primary, which consists of many simultaneously independent direct transceiver pairs. The existence of a secondary eavesdropper, which attempts to hear confidential information, results in secure communication to be needful. The PUs’ interference forces low secondary SIRs. The secondary power constraint according to PUs causes the QoS to diminish, especially when the PUs transmission simultaneously operates. In this paper, we derive the closed-form of end-to-end multi-hop secrecy outage probability expression with independent non-identically distributed (i.n.i.d) Rayleigh fading. Furthermore, the secondary intercept probability is derived. Combining the outage probability, we present the security-reliability of the system. Besides, the impact of different numbers of primary transceivers on end-to-end multi-hop outage probability is investigated. Finally, our theoretical results verified via extensive Monte Carlo simulations.

Appendices

Appendices

1.1 Appendix A

Proof of Proposition 1 in (15)

From (3), denote ${\vartheta _i}\left( \upsilon \right) {=}\Pr \! \left( \!{\frac{{{M_i}}}{{\sum \nolimits _{j {=} 1,j \ne i}^{L^{\phantom {\frac{.}{.}}}} {\left( {{M_j}} \right) }{+}{M_{L {+} 1}} {+} 1}} {\le } \upsilon }\!\right) ,$ where ${M_i} \buildrel \varDelta \over ={\varOmega _i}{\kappa _{i,i}}$, ${M_j} \buildrel \varDelta \over ={\varOmega _i}{\kappa _{j,i}}$, ${M_{L + 1}} \buildrel \varDelta \over ={\varDelta _{k - 1}}{\varpi _{k - 1,i}}$, $M \buildrel \varDelta \over =\sum \nolimits _{j = 1,j \ne i}^L{{M_j}}+{M_{L + 1}} = \sum \nolimits _{a = 1,a \ne i}^{L + 1}{{M_a}}.$ Using the law of total probability in [37, Lemma 1], the ${f_{M,i}}\left( x \right)$ is given by

$$\begin{aligned} {f_{M,i}}\left( x \right) = \prod \limits _{a = 1,a \ne i}^{L + 1}{{\beta _{{M_a}}}}\sum \limits _{a = 1,a \ne i}^{L +1} {\frac{{{e^{ - {\beta _{{M_a}}}.x}}}}{{\prod \nolimits _{b = 1,b \ne a,b \ne i}^{L + 1} {\left( {{\beta _{{M_b}}} - {\beta _{{M_a}}}} \right) } }}}, \end{aligned}$$

(A.1)

where ${\beta _{{M_i}}} = {\delta _{i,i}}$, ${\beta _{{M_{L +1}}}} = {\varpi _{k - 1,i}}$, ${\beta _{{M_a}}} ={\delta _{a,i}}$. With the assistance of [41, 4.20], we easily find ${f_{M + 1,i}}\left( x \right)$. Next, the ${F_{M +1,i}} \left( x \right)$ can be derived by integration the ${f_{M+1,i}} \left( x \right)$.

$$\begin{aligned} {\vartheta _i}\left( \upsilon \right) = 1 - \int \limits _\upsilon ^\infty {{f_{{M_i}}}\left( x \right) .} \Pr \left( {M < \frac{{{M_i} - \upsilon }}{\upsilon }} \right) .dx. \end{aligned}$$

(A.2)

After some algebra and changing variables, we have

$$\begin{aligned} {\vartheta _i}\left( \upsilon \right) =1- \prod \limits _{j = 1,j \ne i}^{L +1}{{\beta _{{M_j}}}} \sum \limits _{a =1,a \ne i}^{L + 1}\frac{{{e^{ - \;{\beta _{{M_i}}} \,\upsilon }}}}{{\left( {\upsilon {\beta _{{M_i}}}+{\beta _{{M_a}}}} \right) \prod \nolimits _{b = 1,b \ne a,b \ne i}^{L + 1}{\left( {{\beta _{{M_b}}}-{\beta _{{M_a}}}} \right) } }}. \end{aligned}$$

(A.3)

Applying the complementary probability theory, $1-{\vartheta _i}\left( \upsilon \right)$ is the success probability on ith pair. Therefore, $1-\prod \nolimits _{i = 1}^L \left( {1-{\vartheta _i}\left( \upsilon \right) } \right)$ is the primary outage, on (15).

1.2 Appendix B

Proof of Proposition 2 in (18)

Substituting (5), (6), (7), the (13) is equivalent to

$$\begin{aligned} {\mathrm{SO}}{{\mathrm{P}}_k}\left( \xi \right) = Pr\left( {\frac{{1+{{{\varDelta _{k - 1}}{\varphi _k}} \Bigg /{\left( {\sum \nolimits _{i = 1}^L {{\varOmega _i}{\omega _{i,k}}}+1} \right) }}}}{{1+{{{\varDelta _{k - 1}}{\chi _k}} \Bigg / {\left( {\sum \nolimits _{i = 1}^L {{\varOmega _i}{\theta _i}}+1} \right) }}}} \le \xi } \right) , \end{aligned}$$

(B.1)

where $\xi = {2^{K{C_{th}}}}$. We can rewrite (B.1) as

$$\begin{aligned} {F_{\xi ,k}}\left( \xi \right) = \Pr \left( \frac{1 + X/\left( {Y+ 1} \right) }{1 + \hat{X}/\left( {\hat{Y} + 1} \right) }< \xi \right) = \Pr \left( {\frac{U}{V} < \xi } \right) , \end{aligned}$$

(B.2)

where $X = {\varDelta _{k - 1}}{\varphi _k}$, $\hat{X} = {\varDelta _{k - 1}}{\chi _k}$ have the mean ${\varepsilon _k},{\eta _k}$. $Y = \sum \nolimits _{i = 1}^L {{Y_i}} ,\hat{Y} = \sum \nolimits _{i = 1}^L {{{\hat{Y}}_i}}$, with ${Y_i} = {\varOmega _i}{\omega _{i,k}}$, ${\hat{Y}_i} = {\varOmega _i}{\theta _i}$, are ${\tau _{i,k}},{\sigma _i}$, respectively. We derive the representative $\Pr \left( {U = 1+X/\left( {Y+1} \right) <u} \right)$ in details. Based on [37, 12], [41, 4.20], we obtain the $\Pr \left( {U \le u} \right)$ expression as follows (B.3), (B.4)

$$\begin{aligned}&{F_U}\left( u \right) = \left\{ \begin{array}{ll} 1 - \left( \prod \limits _{i = 1}^L \tau _{i,k}\right) .\sum \limits _{m = 1}^L \frac{e^{-\;{\varepsilon _k} \left( u - 1\right) }}{\left( \tau _{m,k}+\left( u-1\right) \varepsilon _k\right) .\sum \nolimits _{a = 1,a \ne m}^L \left( \tau _{a,k}-\tau _{m,k}\right) }, &{} u \ge 1\\ 0, &{} u < 1\end{array}\right. \end{aligned}$$

(B.3)

$$\begin{aligned}&f_{\hat{Y} + 1}(y) = {f_{\underbrace{{{\hat{Y}}_1} + {{\hat{Y}}_2} + \cdots + {{\hat{Y}}_L}}_{\hat{Y}} + 1}}(y)\nonumber \\&\quad = \left( {\prod \limits _{i = 1}^L {{\sigma _i}} } \right) .\sum \limits _{n = 1}^L {\frac{{{e^{ - \;{\sigma _n}\left( {y - 1} \right) }}}}{{\prod \nolimits _{b = 1,b \ne n}^L {\left( {{\sigma _b} - {\sigma _n}} \right) } }}}. \end{aligned}$$

(B.4)

Let’s denote $T = \frac{{\hat{X}}}{{\hat{Y}+1}}$, $V = T+1$. We identified ${f_T}\left( t \right)$ by exploiting [42, 21] and solved the integration by [40, 3.381.4]. Afterwards, we apply [41, 4.20] to exchange between T and V random variables. We obtain

$$\begin{aligned} {f_V}\left( v \right) = \left\{ \begin{array}{ll} {\eta _k}\prod \limits _{i = 1}^L {{\sigma _i}} \sum \limits _{n = 1}^L {{e^{{\sigma _n}}} \frac{{{{\left( {{\eta _k}\left( {v - 1} \right) + {\sigma _n}} \right) }^{ - 2}}}}{{\prod \nolimits _{b = 1,b \ne n}^{L^{\phantom {\frac{.}{.}}}} {\left( {{\sigma _b} - {\sigma _n}} \right) } }}} , &{} v\ge 1\\ 0. &{} v<1 \end{array}\right. \end{aligned}$$

(B.5)

We exploit ${F_{\xi ,k}}\left( \xi \right) \!= \!{F_{U/V}}\left( \xi \right) \!=\! \int \nolimits _1^\infty {{f_V}\left( v \right) .} {F_U} \left( {v\xi } \right) dv,$ derived from  [43, 6.42, 6.43]. The result shows in (B.6). Next, we can find the results of the ${Q_i},\;(i = 1,2,3,4)$, in (B.7) by [40, 3.351.4, 3.353.1, 3.352.2]. Substituting (B.7) to  (B.6), we obtain (19), and substituting (19) to  (18), we have ${\mathrm{SO}}{{\mathrm{P}}_{{\mathrm{e2}}e}}$.

$$\begin{aligned} F_{\xi ,k}\left( \xi \right)&= 1 - \frac{e^{\varepsilon _k}}{\varepsilon _k} \prod \limits _{i = 1}^L \tau _{i,k}\prod \limits _{i = 1}^L \sigma _i \sum \limits _{n = 1}^L \sum \limits _{m = 1}^L\nonumber \\&\quad \times \,\frac{\frac{e^{\sigma _n}}{\xi .\eta _k}}{\prod \nolimits _{b = 1,b \ne n}^L\left( \sigma _b-\sigma _n\right) \prod \nolimits _{a = 1,a \ne m}^L \left( {{\tau _{a,k}} - {\tau _{m,k}}} \right) } \nonumber \\&\quad \times \,\underbrace{\xi \eta _k^2\int \nolimits _1^\infty \frac{e^{-\varepsilon _kvz}\left( \frac{1}{vz +\frac{\tau _{m,k}}{\varepsilon _k}- 1}\right) }{\left( \eta _k\left( v-1\right) +\sigma _n\right) ^{2}}dv}_{\mathbb {Q}\left( \xi \right) }, \end{aligned}$$

(B.6)

$$\begin{aligned}&{ where}\, \mathbb {Q}\left( \xi \right) \nonumber \\&\!\quad = \left\{ \begin{array}{ll} \overbrace{\int \limits _1^\infty {\frac{{{e^{ - \;\mu v}}}}{{{{\left( {v {+} \varPhi } \right) }^3}}}} dv}^{{Q_4}} &{} \ \ \varPhi = \varUpsilon \\ - {\alpha _1}.\overbrace{\int \limits _1^\infty {\frac{{v.{e^{ - \mu v}}}}{{{{\left( {v {+} \varUpsilon } \right) }^2}}}dv} }^{{Q_1}} {+} {\alpha _2}.\overbrace{\int \limits _1^\infty {\frac{{{e^{ - \mu v}}}}{{{{\left( {v {+} \varUpsilon } \right) }^2}}}dv} }^{{Q_2}} {+} {\alpha _1}.\overbrace{\int \limits _1^\infty {\frac{{{e^{ - \mu v}}}}{{\left( {v {+} \varPhi } \right) }}dv}}^{{Q_3}} &{}\ \ { otherwise} \end{array}\right. \end{aligned}$$

(B.7)

1.3 Appendix C

Proof of Proposition 3 in (22)

Next, from (3), we consider the ${\mathrm{O}}{{\mathrm{P}}_k} =\Pr \left( {\frac{I}{{H+1}} < {\gamma _{th}}} \right)$, where $I={\varDelta _{k - 1}}{\varphi _k},H = {H_1}+{H_2}...+{H_L} =\sum \nolimits _{i = 1}^L {{\varOmega _i}{\omega _{i,k}}}$,

$$\begin{aligned} {f_H}\left( y \right) = \prod \limits _{i = 1}^L {{\tau _{i,k}}} \sum \limits _{i = 1}^L {\frac{{{e^{ - {\tau _{i,k}}.y}}}}{{\prod \nolimits _{j = 1,j \ne i}^L {\left( {{\tau _{j,k}} - {\tau _{i,k}}} \right) } }}}. \end{aligned}$$

(C.1)

Using the same methodology with the first proposition, we receive the ${\mathrm{O}}{{\mathrm{P}}_k}$ as follows

$$\begin{aligned} {\mathrm{O}}{{\mathrm{P}}_k} = 1-\prod \limits _{i = 1}^L \left( {{\tau _{i,k}}} \right) \sum \limits _{i = 1}^L \frac{e^{-\varepsilon _k\gamma _{th}}}{\left( {{\tau _{i,k}}+{\varepsilon _k}.{\gamma _{th}}} \right) \prod \nolimits _{j = 1,j \ne i}^L \left( {{\tau _{j,k}}-{\tau _{i,k}}} \right) }. \end{aligned}$$

(C.2)

Afterwards, the ${\mathrm{O}}{{\mathrm{P}}_{e2e}}$ in (24) is derived following the substitution of ${\mathrm{O}}{{\mathrm{P}}_k}$ with (C.2) in (23).

1.4 Appendix D

From (4), let us denote

$$\begin{aligned} {\mathrm{I}}{{\mathrm{P}}_k} = \Pr \left( {\frac{P}{{Q+1}} \ge {\gamma _{th}}} \right) = 1-\Pr \left( {\frac{P}{{Q+1}} < {\gamma _{th}}} \right) , \end{aligned}$$

(D.1)

where $P = {\varDelta _{k - 1}}{\chi _k},\;Q = {Q_1}+{Q_2}+\cdots +{Q_L} =\sum \nolimits _{i = 1}^L {{\varOmega _i}{\theta _i}}$. Likewise, the ${f_Q}\left( y \right)$ can be written as

$$\begin{aligned} {f_Q}\left( y \right) = \prod \limits _{i = 1}^L {{\eta _k}} .\sum \limits _{i = 1}^L \frac{e^{-\sigma _iy}}{\prod \nolimits _{j = 1,j \ne i}^L\left( \sigma _j-\sigma _i\right) }. \end{aligned}$$

(D.2)

Applying similar way above, we obtain the expression in (26).