A stochastic differential equation SIS epidemic model with two correlated Brownian motions

Abstract

In this paper, we introduce two perturbations in the classical deterministic susceptible-infected-susceptible epidemic model with two correlated Brownian motions. We consider two perturbations in the deterministic SIS model and formulate the original model as a stochastic differential equation with two correlated Brownian motions for the number of infected population, based on the previous work from Gray et al. (SIAM J Appl Math 71(3):876–902, 2011) and Hening and Nguyen (J Math Biol 77:135–163, 2017. https://doi.org/10.1007/s00285-017-1192-8). Conditions for the solution to become extinction and persistence are then stated, followed by computer simulation to illustrate the results.

1 Introduction

Human beings never stop fighting against deadly disease, and nowadays, epidemic models are the most common means to study population dynamics in epidemic problems. For example, the classic Kermack–Mckendrick model [1] is a sufficient model to describe simple epidemics that provide immunity for those infected people after recovery, while the classical susceptible-infected-susceptible (SIS) models (1) can be used to explain disease transmission.

$$\begin{aligned} \,{\mathrm {d}}I(t)=[\beta (N-I(t))I(t)-(\mu +\gamma )I(t)]\,{\mathrm {d}}t , \end{aligned}$$

(1)

with initial value $I_0\in (0,N)$. Specifically, S(t) and I(t) are the numbers of susceptibles and infected at time t. N is the total size of the population where the disease is found. $\mu$ is the per capita death rate, and $\gamma$ represents the rate of infected individuals becoming cured, while $\beta$ is the per capita disease contact rate.

Moreover, environmental noises, such as white noise and telegraph noise, are taken into consideration in deterministic models to help us understand dynamic behaviours in epidemic models. There are many examples studying the behaviour of both deterministic [1, 2] and stochastic [3,4,5,6] SIS epidemic models. Different medical means on controlling the disease are also mathematically applied in SIS model such as [7,8,9]. Also, Gray et al. [10] apply a perturbation on the disease transmission coefficient in SIS model.

$$\begin{aligned} {\tilde{\beta }} \,{\mathrm {d}}t=\beta \,{\mathrm {d}}t+\sigma _1\,{\mathrm {d}}B_3(t) \end{aligned}$$

However, to the best of our knowledge, there is not enough work on incorporating white noise with $\mu +\gamma$ in the SIS epidemic model (1). Here, we suppose that the variance of estimating $\mu +\gamma$ is proportional to the number of susceptible population. Consequently, we then add another perturbation on per capita death rate and infectious period $\mu +\gamma$.

$$\begin{aligned} ({\tilde{\mu }}+{\tilde{\gamma }})\,{\mathrm {d}}t=(\mu +\gamma )\,{\mathrm {d}}t+\sigma _2\sqrt{N-I(t)}\,{\mathrm {d}}B_4(t) \end{aligned}$$

We then obtain that

$$\begin{aligned} \,{\mathrm {d}}I(t)&= [\beta (N-I(t))I(t)-(\mu +\gamma )I(t)]\,{\mathrm {d}}t \nonumber \\&\quad +\sigma _1I(t)(N-I(t))\,{\mathrm {d}}B_3(t) \nonumber \\&\quad -\sigma _2I(t)\sqrt{N-I(t)}\,{\mathrm {d}}B_4(t) \end{aligned}$$

(2)

with initial value $I(0)=I_0 \in (0,N)$, $B_3$ and $B_4$ are two independent Brownian motions.

Moreover, it is necessary to consider if there is a relationship between these two perturbation. And if we use the same data in real world to construct these two Brownian motions, they are very likely to be correlated [11]. And there is the previous work focusing on correlation of Brownian motions in dynamic systems. Hu et al. [12] consider two correlative stochastic disturbances in the form of Gaussian white noise in an epidemic deterministic model constructed by Roberts and Jowett [13]. Also, Hening and Nguyen [14] construct a stochastic Lotka–Volterra food chain system by introducing n number of correlated Brownian motions into the deterministic food chain model. n is the total species number in the food chain and they use a coefficient matrix to convert the vector of correlated Brownian motions to a vector of independent standard Brownian motions. Inspired by Emmerich [11], Hu et al. [12] and Hening and Nguyen [14], we are going to replace $B_3$ and $B_4$ by two correlated Brownian motions to introduce correlation of noises in SIS epidemic model. Considering two correlated Brownian motions, one with linear diffusion coefficient and the other with Hölder continuous diffusion coefficient, is clearly different from other work on stochastic SIS model. Though Hölder continuous diffusion coefficient and correlations of white noises are often involved in stochastic financial and biological models [15], there is no related work based on deterministic SIS model. As a result, this paper aims to fill this gap.

We now consider $B_3$ and $B_4$ in our model (2) to be correlated. Replace $B_3$ and $B_4$ by correlated Brownian motions $E_1$ and $E_2$.

$$\begin{aligned} \,{\mathrm {d}}I(t)&= [\beta (N-I(t))I(t)-(\mu +\gamma )I(t)]\,{\mathrm {d}}t \nonumber \\&\quad +\sigma _1I(t)(N-I(t))\,{\mathrm {d}}E_1(t) \nonumber \\&\quad -\sigma _2I(t)\sqrt{N-I(t)}\,{\mathrm {d}}E_2(t) \end{aligned}$$

(3)

Note that $E_1$ and $E_2$ can be written as

$$\begin{aligned} (E_1,E_2)^\mathrm{T}=A(B_1,B_2)^\mathrm{T} \end{aligned}$$

$(B_1,B_2)$ is a vector of independent Brownian motions and A is the coefficient matrix

$$\begin{aligned} A= \begin{bmatrix} a_1&0 \\ a_2&a_3 \end{bmatrix},\ a_1, a_2, a_3 \, \text {are constants} \end{aligned}$$

So we have

$$\begin{aligned}&\,{\mathrm {d}}E_1(t)=a_1\,{\mathrm {d}}B_1(t), \nonumber \\&\,{\mathrm {d}}E_2(t)=a_2\,{\mathrm {d}}B_1(t)+a_3 B_2(t) \end{aligned}$$

(4)

Also

$$\begin{aligned} \,{\mathrm {d}}E_1 \,{\mathrm {d}}E_2 = a_1 a_2 \,{\mathrm {d}}t \end{aligned}$$

which gives the correlation of $E_1$ and $E_2$

$$\begin{aligned} \rho =a_1a_2, \ 0<\left| \rho \right| <1 \end{aligned}$$

Note that when $\rho =0$, $B_1$ and $B_2$ are independent Brownian motion.

Substituting (4) into (3), we have

$$\begin{aligned} \,{\mathrm {d}}I(t)&= [\beta (N-I(t))I(t)-(\mu +\gamma )I(t)]\,{\mathrm {d}}t \nonumber \\&\quad +[a_1 \sigma _1I(t)(N-I(t)) \nonumber \\&\quad \qquad -a_2\sigma _2I(t)\sqrt{N-I(t)}]\,{\mathrm {d}}B_1(t) \nonumber \\&\quad -a_3\sigma _2I(t)\sqrt{N-I(t)}\,{\mathrm {d}}B_2(t) \end{aligned}$$

(5)

with initial value $I(0)=I_0 \in (0,N)$ and this is our new model. Throughout this paper, unless otherwise specified, we let $(\Omega ,\{{\mathcal {F}}_t\}_{t\geqslant 0},{\mathbb {P}})$ be a complete probability space with a filtration $\{{\mathcal {F}}_t\}_{t\geqslant 0}$ satisfying the usual conditions. We also define ${\mathcal {F}}_{\infty }=\sigma (\bigcup _{t\geqslant 0}{\mathcal {F}}_t)$, i.e. the $\sigma$-algebra generated by $\bigcup _{t\geqslant 0}{\mathcal {F}}_t$. Let $B(t)=(B_1(t),B_2(t)^\mathrm{T}$ be a two-dimensional Brownian motion defined on this probability space. We denote by ${\mathbb {R}}_+^2$ the positive cone in ${\mathbb {R}}^2$, that is ${\mathbb {R}}^2_+=\{x\in {\mathbb {R}}^2:x_1>0,x_2>0 \}$. We also set $\inf \emptyset =\infty$. If A is a vector or matrix, its transpose is denoted by $A^\mathrm{T}$. If A is a matrix, its trace norm is $|A|=\sqrt{trace (A^\mathrm{T}A)}$ while its operator norm is $||A||=\sup \{|Ax|:|x|=1 \}$. If A is a symmetric matrix, its smallest and largest eigenvalues are denoted by $\lambda _\mathrm{min}(A)$ and $\lambda _\mathrm{max}(A)$. In the following sections, we will focus on the long-time properties of the solution to model (5).

2 Existence of unique positive solution

We firstly want to know if the solution of our model (5) has a unique solution. Also, we need this solution to be positive and bounded within (0, N) because it is meaningless for the number of infected population to exceed the number of whole population. So here we give Theorem 2.1.

Theorem 2.1

If $\mu +\gamma \ge \frac{1}{2} (a_2^2+a_3^2)\sigma _2^2 N$, then for any given initial value $I(0)=I_0 \in (0,N)$, the SDE has a unique global positive solution $I(t) \in (0,N)$ for all $t\ge 0$ with probability one, namely,

$$\begin{aligned} {\mathbb {P}}\{ I(t)\in (0,N),\ \forall t\ge 0 \}=1 \end{aligned}$$

Proof

By the local Lipschitz condition, there must be a unique solution for our SDE (5) for any given initial value. So there is a unique maximal local solution I(t) on $t\in [0,\tau _e)$, where $\tau _e$ is the explosion time [15]. Let $k_0\ge 0$ be sufficient large to satisfy $\frac{1}{k_0}<I_0<N-\frac{1}{k_0}$. For each integer $k\ge k_0$, define the stopping time

$$\begin{aligned} \tau _k=\text {inf}\{t\in [0,\tau _e)\ :I(t)\notin (1/k,N-1/k)\} \end{aligned}$$

Set $\text {inf} \emptyset =\infty$. Clearly, $\tau _k$ is increasing when $k \rightarrow \infty$. And we set $\tau _\infty =\lim _{k\rightarrow \infty }{\tau _k}$. It is obvious that $\tau _\infty \le \tau _e$ almost sure. So if we can show that $\tau _\infty =\infty$ a.s., then $\tau _e=\infty$ a.s. and $I(t) \in (0,N)$ a.s. for all $t \ge 0$.

Assume that $\tau _\infty =\infty$ is not true. Then, we can find a pair of constants $T>0$ and $\epsilon \in (0,1)$ such that

$$\begin{aligned} {\mathbb {P}}\{ \tau _\infty \le T\}>\epsilon \end{aligned}$$

So we can find an integer $k_1\ge k_0$ large enough, such that

$$\begin{aligned} {\mathbb {P}}\{ \tau _k \le T\}\ge \epsilon \ \ \ \ \forall k\ge k_1 \end{aligned}$$

(6)

Define a function $V: (0,N)\rightarrow {\mathbb {R}}_+$ by

$$\begin{aligned} V(x)=-\log {x}-\log {(N-x)}+\log {\frac{N^2}{4}} \end{aligned}$$

and

$$\begin{aligned} V_x=-\frac{1}{x}+\frac{1}{N-x},\ V_{xx}=\frac{1}{x^2}+\frac{1}{(N-x)^2} \end{aligned}$$

Let $f(t)=\beta (N-I(t))I(t)-(\mu +\gamma )I(t)$, $g(t)=(a_1\sigma _1I(t)(N-I(t))-a_2\sigma _2\sqrt{N-I(t)}I(t), -a_3\sigma _2I(t)\sqrt{N-I(t)})$ and $\,{\mathrm {d}}B(t)= (\,{\mathrm {d}}B_1(t), \,{\mathrm {d}}B_2(t))$.

By Ito formula [15], we have, for any $t\in [0,T]$ and any k

$$\begin{aligned} {\mathbb {E}}V(I(t\wedge \tau _k))= & {} V(I_0)+ {\mathbb {E}}\int _0^{t\wedge \tau _k}LV(I(s)) \,{\mathrm {d}}s \nonumber \\&+\,{\mathbb {E}}\int _0^{t\wedge \tau _k} V_xg(s) \,{\mathrm {d}}B(s) \end{aligned}$$

(7)

${\mathbb {E}}\int _0^{t\wedge \tau _k} V_xg(s) \,{\mathrm {d}}B(s)=0$. Also it is easy to show that

$$\begin{aligned} LV(x)&=-\beta (N-x)+(\mu +\gamma ) \\&\quad +\beta x-(\mu +\gamma )\frac{x}{N-x} \\&\quad +\frac{1}{2} \left( \frac{1}{x^2}+\frac{1}{(N-x)^2}\right) \\&\quad \left[ a_1^2\sigma _1^2x^2(N-x)^2 \right. \\&\qquad +(a_2^2+a_3^2)\sigma _2^2x^2(N-x) \\&\qquad \left. -2\rho \sigma _1\sigma _2x^2(N-x)^\frac{3}{2}\right] \\&\le -\beta (N-x)+(\mu +\gamma )+\beta x \\&\quad +\frac{1}{2}a_1^2\sigma _1^2 (N-x)^2 \\&\quad +\frac{1}{2}a_1^2\sigma _1^2x^2+\frac{\mu +\gamma }{N} \sigma _2^2(N-x) \\&\le C \end{aligned}$$

C is a constant when $\mu +\gamma \ge \frac{1}{2}(a_2^2+a_3^2)\sigma _2^2 N$ and $x\in (0,N)$.

Then, we have

$$\begin{aligned} {\mathbb {E}}V(I(t\wedge \tau _k))&\le V(I_0)+ {\mathbb {E}}\int _0^{t\wedge \tau _k}C \,{\mathrm {d}}s\nonumber \\&\le V(I_0)+Ct \end{aligned}$$

(8)

which yields that

$$\begin{aligned} {\mathbb {E}}V(I(T\wedge \tau _k)) \le V(I_0)+CT \end{aligned}$$

(9)

Set $\Omega _k=\{\tau _k \le T\}$ for $k\ge k_1$ and we have ${\mathbb {P}}(\Omega _k)\ge \epsilon$. For every $\omega \in \Omega _k$, $I(\tau _k, \omega )$ equals either 1 / k or $N-1/k$ and we have

$$\begin{aligned} V(I(\tau _k,\omega ))= \log {\frac{N^2}{4(N-1/k)1/k}} \end{aligned}$$

Hence,

$$\begin{aligned} \infty > V(I_0)+CT&\ge {\mathbb {E}}[{\mathbb {I}}_{\Omega _k}(\omega )V(I(\tau _k,\omega ))]\\&\ge {\mathbb {P}}(\Omega _k)\log {\frac{N^2}{4(N-1/k)1/k}}\\&=\epsilon \log {\frac{N^2}{4(N-1/k)1/k}} \end{aligned}$$

letting $k \rightarrow \infty$ will lead to the contradiction

$$\begin{aligned} \infty >V(I_0)+CT= \infty \end{aligned}$$

So the assumption is not reasonable and we must have $\tau _\infty =\infty$ almost sure, whence the proof is now complete. Compared to the result from Gray et al. [10], the condition is now related to $(a_2^2+a_3^2)$. The square root terms are the reasons for us to give initial conditions in this section: when $N-I(t)\rightarrow 0$, $\sqrt{N-I(t)}$ changes rapidly. This can also be an explanation to the readers that the condition is dependent on $a_2$ and $a_3$ instead of $\rho =a_1a_2$. $\square$

3 Extinction

The previous section has already provided us with enough evidence that our model has a unique positive bounded solution. However, we do not know under what circumstances the disease will die out or persist and they are of great importance in study of epidemic models. In this section, we will discuss the conditions for the disease to become extinction in our SDE model (5). Here, we give Theorem 3.1 and we will discuss persistence in the next section.

3.1 Theorem and proof

Theorem 3.1

Given that the stochastic reproduction number of our model

$R_0^S := \frac{\beta N}{\mu +\gamma }- \frac{a_1^2\sigma _1^2N^2 +(a_2^2+a_3^2) \sigma _2^2N-2 \rho \sigma _1\sigma _2N^\frac{3}{2}}{2(\mu +\gamma )}<1$, then for any given initial value $I(0)=I_0\in (0,N)$, the solution of SDE obeys

$$\begin{aligned} \limsup _{t\rightarrow \infty }{ \frac{1}{t}\log {I(t)}}<0 \ a.s. \end{aligned}$$

(10)

if one of the following conditions is satisfied

• $\frac{1}{2}(a_2^2+a_3^2)\sigma _2^2\ge \beta$ and $-1<\rho <0$

• $\frac{1}{2}(a_2^2+a_3^2)\sigma _2^2\ge \beta +\frac{3}{2}\rho \sigma _1\sigma _2 \sqrt{N}-a_1^2\sigma _1^2N^2$ and $3a_2\sigma _2\ge 4\sqrt{N}a_1\sigma _1$

• $\frac{1}{2}(a_2^2+a_3^2)\sigma _2^2< \beta \wedge (\beta +\frac{3}{2}\rho \sigma _1\sigma _2 \sqrt{N}-a_1^2\sigma _1^2N)$

• $\frac{1}{2}(a_2^2+a_3^2)\sigma _2^2\ge \beta +\frac{9}{16}a_2^2\sigma _2^2$ and $0<\rho <1$

namely, I(t) will tend to zero exponentially a.s. And the disease will die out with probability one.

Proof

Here, we use Ito formula

$$\begin{aligned} \frac{\log {I(t)}}{t}= & {} \frac{\log {I_0}}{t}+\frac{1}{t} \int _0^t L{\tilde{V}}(I(s)) \,{\mathrm {d}}s \nonumber \\&+\frac{1}{t}\int _0^t \frac{1}{I(s)}g(I(s))\,{\mathrm {d}}B(s) \end{aligned}$$

(11)

and according to the large number theorem for martingales [15], we must have

$$\begin{aligned} \limsup _{t\rightarrow \infty }{\frac{1}{t}\int _0^t \frac{1}{I(s)}g(I(s))\,{\mathrm {d}}B(s)}=0 \end{aligned}$$

So if we want to prove $\limsup _{t\rightarrow \infty }{ \frac{1}{t}\log {I(t)}}<0$ almost sure, we need to find the conditions for $L{\tilde{V}}(x)$ to be strictly negative in (0, N). $L{\tilde{V}}$ is defined by

$$\begin{aligned} L{\tilde{V}}&=\frac{1}{x} [\beta (N-x)-(\mu +\gamma )]x \nonumber \\&\quad - \frac{1}{2x^2}\left[ a_1^2\sigma _1^2x^2(N-x)^2 \right. \nonumber \\&\qquad \qquad +(a_2^2+a_3^2) \sigma _2^2x^2(N-x) \nonumber \\&\qquad \qquad \left. -2\rho \sigma _1\sigma _2x^2(N-x)^\frac{3}{2}\right] \nonumber \\&=\beta (N-x)-(\mu +\gamma )-\frac{1}{2}a_1^2\sigma _1^2(N-x)^2 \nonumber \\&\quad - \frac{1}{2}(a_2^2+a_3^2)\sigma _2^2(N-x)+\rho \sigma _1\sigma _2(N-x)^\frac{3}{2} \end{aligned}$$

(12)

And it is clear that

$$\begin{aligned} L{\tilde{V}}(N)=-\,(\mu +\gamma )<0 \end{aligned}$$

and

$$\begin{aligned} L{\tilde{V}}(0)<0 \end{aligned}$$

is ensured by $R_0^S<1$. However, we do not know the behaviour of $L{\tilde{V}}$ in (0, N) and it is no longer quadratic as [10], which is very easy to analyse. As a result, we derive the first derivative of $L{\tilde{V}}$.

$$\begin{aligned} \frac{\,{\mathrm {d}}L{\tilde{V}}}{\,{\mathrm {d}}x}= & {} -\beta +a_1^2\sigma _1^2(N-x) +\frac{1}{2}(a_2^2+a_3^2)\sigma _2^2 \nonumber \\&-\frac{3}{2}\rho \sigma _1 \sigma _2\sqrt{N-x} \end{aligned}$$

(13)

This is a quadratic function of $z=\sqrt{N-x}$. So by assuming $D(z)=\frac{\,{\mathrm {d}}L{\tilde{V}}}{\,{\mathrm {d}}x}$, we have

$$\begin{aligned} D(z)=a_1^2\sigma _1^2z^2-\frac{3}{2}\rho \sigma _1\sigma _2z+ \frac{1}{2}(a_2^2+a_3^2)\sigma _2^2-\beta \end{aligned}$$

(14)

where $z\in (0, \sqrt{N})$. The axis of symmetry of (14) is ${\hat{z}}=\frac{3a_2\sigma _2}{4a_1\sigma _1}$

Here, we are going to discuss different cases for (14).

Case 1 If $\frac{1}{2}(a_2^2+a_3^2)\sigma _2^2\ge \beta$ and $-1<\rho <0$ (${\hat{z}}<0$)

From the behaviour of the quadratic function (14), we know that the value of this function will be always positive in (0, N). This means $L{\tilde{V}}$ increases when x increases. As $L{\tilde{V}}(N)<0$, We have $L{\tilde{V}}\le L{\tilde{V}}(N)<0$. This leads to extinction.

Case 2 If $\frac{1}{2}(a_2^2+a_3^2)\sigma _2^2\ge \beta$, $D(\sqrt{N})\ge 0$ and ${\hat{z}}=\frac{3a_2\sigma _2}{4a_1\sigma _1}\ge \sqrt{N}$

In this case, the value of D(z) is always positive within $z \in (0, \sqrt{N})$, which leads to the similar result in Case 1. So we have

$$\begin{aligned} \frac{1}{2}(a_2^2+a_3^2)\sigma _2^2\ge \beta +\frac{3}{2}\rho \sigma _1\sigma _2 \sqrt{N}-a_1^2\sigma _1^2N \end{aligned}$$

with ${\hat{z}}>\sqrt{N}$

Case 3 If $\frac{1}{2}(a_2^2+a_3^2)\sigma _2^2< \beta$ and $D(\sqrt{N})<0$

This condition makes sure that the value of D(z) is strictly negative in $(0,\sqrt{N})$, which indicates that $L{\tilde{V}}$ decreases when x increases. With $L{\tilde{V}}(N)<0$ and $L{\tilde{V}}(0)<0$, this case results in extinction and we have

$$\begin{aligned} \frac{1}{2}(a_2^2+a_3^2)\sigma _2^2< \beta \wedge \left( \beta +\frac{3}{2}\rho \sigma _1\sigma _2 \sqrt{N}-a_1^2\sigma _1^2N^2\right) \end{aligned}$$

Case 4 If $\Delta =\frac{9}{4}(a_1a_2 \sigma _1\sigma _2)^2-4a_1^2 \sigma _1^2[\frac{1}{2}(a_2^2+a_3^2)\sigma _2^2-\beta ]\le 0$

We have $\frac{1}{2}(a_2^2+a_3^2)\sigma _2^2\ge \beta +\frac{9}{16}a_2^2\sigma _2^2$. In this case, D(z) will be positive in $(0,\sqrt{N})$, so $L{\tilde{V}}$ increases when x increases. Similarly, extinction still maintains in this case.

In the deterministic SIS model, we have the result that if $R_0^D<1$, the disease will die out. However, from our results in this section, we can see that our stochastic reproduction number $R_0^S$ is always less that the deterministic reproduction number $R_0^D=\frac{\beta N}{\mu +\gamma }$, which indicates that the noise and correlation in our model help expand the conditions of extinction. For those parameters that will not cause the dying out of disease in the deterministic SIS model as well as Gray’s model [10], extinction will become possible if we consider the new perturbation and the correlation. $\square$

3.2 Simulation

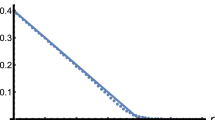
In this section, we use Euler–Maruyama Method [10, 16] implemented in R to simulate the solutions in those 4 cases. For each case, we initially give a complete set of parameter to satisfy not only the extinction conditions, but also $\mu +\gamma \ge \frac{1}{2} (a_2^2+a_3^2)\sigma _2^2 N$ to make sure the uniqueness and boundedness of solutions. Also, both large and small initial values are used in all 4 cases for better illustration. We then choose the step size $\Delta =0.001$ and plot the solutions with 500 iterations. Throughout the paper, we shall assume that the unit of time is one day and the population sizes are measured in units of 1 million, unless otherwise stated (Figs. 1 2, 3, 4).

Case 1

$$\begin{aligned}&N=100,\ \beta =0.4\ \mu +\gamma =45,\\&\sigma _1=0.02,\ \sigma _2=0.95 \\&a_1=2, a_2=-0.4, a_3=0.9, \\&R_0^S<1, \rho =-0.8\in (-1,0) \end{aligned}$$

Fig. 1

Extinction case 1

Case 2

$$\begin{aligned}&N=100,\ \beta =0.4\ \mu +\gamma =45,\\&\sigma _1=0.02,\ \sigma _2=0.95 \\&a_1=1.4, a_2=0.4, a_3=0.9, \\&R_0^S<1, \rho =0.54 \in (0,1) \end{aligned}$$

Fig. 2

Extinction case 2

Case 3

$$\begin{aligned}&N=100,\ \beta =0.4\ \mu +\gamma =45,\\&\sigma _1=0.02,\ \sigma _2=0.05 \\&a_1=0.8, a_2=0.5, a_3=1.6, R_0^S=0.852638<1 \end{aligned}$$

Fig. 3

Extinction case 3

Case 4

$$\begin{aligned}&N=100,\ \beta =0.4\ \mu +\gamma =45,\\&\sigma _1=0.02,\ \sigma _2=0.9 \\&a_1=3, a_2=-0.3, a_3=1, R_0^S<1 \end{aligned}$$

Fig. 4

Extinction case 4

The simulation results are clearly supporting our theorem and illustrating the extinction of the disease. Note that these conditions are not all the conditions for extinction. We only consider the situation that D(z) is either strictly positive or strictly negative. Otherwise, there will be much more complicated cases when $L{\tilde{V}}$ is not monotonic in (0, N).

4 Persistence

In this section, we firstly define persistence in this paper as there are many definitions in stochastic dynamic models to define persistence [3, 4, 10, 15, 17,18,19,20]. However, our model (5) is based on [10]. As a result, we want to give a similar definition of persistence in our model (5). So here we give Theorem 4.1 to give a condition for the solution of (5) oscillating around a positive level.

4.1 Theorem and proof

Theorem 4.1

If $R_0^S>1$, then for any given initial value $I(0)=I_0 \in (0,N)$, the solution of (5) follows

$$\begin{aligned} \limsup _{t\rightarrow \infty }{I(t)}\ge \xi \text { and } \liminf _{t\rightarrow \infty }{I(t)}\le \xi \ \ a.s. \end{aligned}$$

(15)

$\xi$ is the only positive root of ${\tilde{L}}V=0$ in (0, N). I(t) will be above or below the level $\xi$ infinitely often with probability one.

Proof

When $R_0^S>1$, recall that

$$\begin{aligned} L{\tilde{V}}= & {} \beta (N-x)-(\mu +\gamma )-\frac{1}{2}a_1^2\sigma _1^2 (N-x)^2 \\&-\frac{1}{2}(a_2^2+a_3^2)\sigma _2^2(N-x)+\rho \sigma _1 \sigma _2(N-x)^\frac{3}{2} \end{aligned}$$

We have $L{\tilde{V}}(0)>0$ which is guaranteed by $R_0^S>1$, $L{\tilde{V}}(N)=-(\mu +\gamma )<0$. As $L{\tilde{V}}(x)$ is a continuous function in (0, N), there must be a positive root of $L{\tilde{V}}(x)=0$ in (0, N). Moreover, from the behaviour of D(z), it is clear that $L{\tilde{V}}$ will either increase to max value and then decrease to minimum, or increase to maximum, decrease to minimum and then increase to $L{\tilde{V}}(N)<0$. So In both cases, $L{\tilde{V}}(x)=0$ will only have one unique positive root $\xi$ in (0, N).

Here, we recall (11)

$$\begin{aligned} \frac{\log {I(t)}}{t}= & {} \frac{\log {I_0}}{t}+\frac{1}{t} \int _0^t L{\tilde{V}}(I(s)) \,{\mathrm {d}}s \\&+\frac{1}{t}\int _0^t \frac{1}{I(s)}g(I(s))\,{\mathrm {d}}B(s) \end{aligned}$$

According to the large number theorem for martingales [15], there is an $\Omega _2\subset \Omega$ with ${\mathbb {P}}\{\Omega _2\}=1$ such that for every $\omega \in \Omega _2$

$$\begin{aligned} \frac{1}{t}\int _0^t \frac{1}{I(s)}g(I(s))\,{\mathrm {d}}B(s)=0 \end{aligned}$$

Now we assume that $\limsup _{t\rightarrow \infty }{I(t)}\ge \xi \ a.s.$ is not true. Then, there must be a small $\epsilon \in (0,1)$ such that

$$\begin{aligned} {\mathbb {P}} \left\{ \limsup _{t\rightarrow \infty }{I(t)}\le \xi -2\epsilon \right\} >\epsilon \end{aligned}$$

(16)

Let $\Omega _1=\{\limsup _{t\rightarrow \infty }{I(t)}\le \xi -2\epsilon \}$, then for every $\omega \in \Omega _1$, there exist $T=T(\omega )$ large enough, such that

$$\begin{aligned} I(t,\omega )\le \xi -2\epsilon +\epsilon =\xi -\epsilon ,\ \text {when} \, t\ge T(\omega ) \end{aligned}$$

which means when $t\ge T(\omega )$, $L{\tilde{V}}(I(t,\omega ))\ge L{\tilde{V}}(\xi -\epsilon )$. Then, we have for any fixed $\omega \in \Omega _1\cap \Omega _2$ and $t\ge T(\omega )$

$$\begin{aligned}&\liminf _{t\rightarrow \infty }{\frac{1}{t}\log {I(t,\omega )}} \\&\quad \ge 0+\lim _{t\rightarrow \infty }{\frac{1}{t} \int _0^{T(\omega )} L{\tilde{V}}(I(s,\omega )) \,{\mathrm {d}}s} \\&\qquad +\lim _{t\rightarrow \infty } \frac{1}{t}L{\tilde{V}}(\xi -\epsilon )(t-T(\omega )) \\&\quad \ge L{\tilde{V}}(\xi -\epsilon )>0 \end{aligned}$$

which yields

$$\begin{aligned} \lim _{t\rightarrow \infty }I(t,\omega )=\infty \end{aligned}$$

(17)

and this contradicts with the assumption (16). So we must have $\limsup _{t\rightarrow \infty }{I(t)}\ge \xi$ almost sure.

Similarly, if we assume that $\liminf _{t\rightarrow \infty }{I(t)}\le \xi \ a.s.$ is not true, then there must be a small $\delta \in (0,1)$ such that

$$\begin{aligned} {\mathbb {P}} \left\{ \liminf _{t\rightarrow \infty }{I(t)}\ge \xi +2\delta \right\} >\delta \end{aligned}$$

(18)

Let $\Omega _3=\{\liminf _{t\rightarrow \infty }{I(t)}\ge \xi +2\delta \}$, then for every $\omega \in \Omega _3$, there exist $T'=T'(\omega )$ large enough, such that

$$\begin{aligned} I(t,\omega )\ge \xi +2\delta -\delta =\xi +\delta ,\ \text {when} \, t\ge T'(\omega ) \end{aligned}$$

Now we fix any $\omega \in \Omega _3\cap \Omega _2$ and when $t\ge T'(\omega )$, $L{\tilde{V}}(I(t,\omega ))\le L{\tilde{V}}(\xi +\delta )$ and so we have

$$\begin{aligned}&\limsup _{t\rightarrow \infty }{\frac{1}{t}\log {I(t,\omega )}} \\&\quad \le 0+\lim _{t\rightarrow \infty }{\frac{1}{t} \int _0^{T'(\omega )}L{\tilde{V}}(I(s,\omega )) \,{\mathrm {d}}s} \\&\qquad +\lim _{t\rightarrow \infty } \frac{1}{t}L{\tilde{V}}(\xi +\delta )(t-T'(\omega )) \\&\quad \le L{\tilde{V}}(\xi +\delta )<0 \end{aligned}$$

which yields

$$\begin{aligned} \lim _{t\rightarrow \infty }I(t,\omega )=0 \end{aligned}$$

(19)

and this contradicts the assumption (18). So we must have $\liminf _{t\rightarrow \infty }{I(t)}\le \xi$ almost sure. $\square$

4.2 Simulation

In this section, we choose the values of our parameter as follows:

$$\begin{aligned}&N=100,\ \beta =0.5,\ \mu +\gamma =45,\\&\sigma _1=0.02,\ \sigma _2=0.05 \end{aligned}$$

In order to prove the generality of our result, we use two different $\rho$, one positive and the other negative.

$$\begin{aligned}&a_1=1, a_2=0.7, a_3=1.6, \rho _1= 0.5>0, \\&R_0^S=1.0581944 \end{aligned}$$

and

$$\begin{aligned}&a_1=-0.1, a_2=0.5, a_3=0.8, \rho _2=-0.46<0, \\&R_0^S=1.108194 \end{aligned}$$

In both cases, we firstly use Newton–Raphson method [21] in R to find a approximation to the roots $\xi$ of both $L{\tilde{V}}$, which are 7.092595 and 9.680572, respectively. Then, we use Euler–Maruyama method [10, 16] implemented in R to plot the solutions of our SDE with both large and small initial values, following by using red lines to indicate the level $\xi$. The step size is 0.001, and 20000 iterations are used in each example. In the following figures, Theorem 4.1. is clearly illustrated and supported (Figs. 5, 6).

Fig. 5

Persistence case 1: $\rho >0$

Fig. 6

Persistence case 2: $\rho <0$

5 Stationary distribution

To find a stationary distribution of our SDE model (5) is of great important. From the simulation of the last section, we can clearly see that the results strongly indicate the existence of a stationary distribution. In order to complete our proof, we need to initially use a well-known result from Khasminskii as a lemma. [22]

Lemma 5.1

The SDE model (1.3) has a unique stationary distribution if there is a strictly proper subinterval (a,b) of (0,N) such that ${\mathbb {E}}(\tau )<\infty$ for all $I_0\in (0,a]\cup [b,N)$, where

$$\begin{aligned} \tau =\inf \{t\ge 0 : I(t)\in (a,b)\} \end{aligned}$$

also,

$$\begin{aligned} \sup _{I_0\in [{\bar{a}},{\bar{b}}]} {\mathbb {E}}(\tau )<\infty \end{aligned}$$

for every interval $[{\bar{a}},{\bar{b}}]\subset (0,N).$

Now we give the following Theorem 5.1 and the proof by using Lemma 6.

5.1 Theorem and proof

Theorem 5.1

If $R_0^S>1$, then our SDE model (5) has a unique stationary distribution.

Proof

Firstly, we need to fix any (a, b) such that,

$$\begin{aligned} 0<a<\xi<b<N \end{aligned}$$

recall the discussion of ${\tilde{LV}}$ in last section, we can see that

$$\begin{aligned} L{\tilde{V}}(x)\ge & {} L{\tilde{V}}(0)\wedge L{\tilde{V}}(a)>0,\text {if } 0<x\le a \end{aligned}$$

(20)

$$\begin{aligned} L{\tilde{V}}(x)\le & {} L{\tilde{V}}(b)\vee L{\tilde{V}}(N)<0 ,\text {if } b\le x<N \end{aligned}$$

(21)

also, recall (11)

$$\begin{aligned} \log {I(t)}=\log {I_0}+ \int _0^t L{\tilde{V}}(I(s)) \,{\mathrm {d}}s+\frac{1}{t}\int _0^t \frac{1}{x}g(x) \end{aligned}$$

and define

$$\begin{aligned} \tau =\inf \{t\ge 0 : I(t)\in (a,b)\} \end{aligned}$$

Case 1 For all $t\ge 0$ and any $I_0\in (0,a]$, use (20) in (11), we have

$$\begin{aligned} {\mathbb {E}}\log {I(t\wedge \tau )}&={\mathbb {E}}\log {I_0}+{\mathbb {E}}\int _0^{t\wedge \tau } L{\tilde{V}}(I(s))\,{\mathrm {d}}s+0 \\&\ge \log {I_0}+ {\mathbb {E}}(L{\tilde{V}}(0)\wedge L{\tilde{V}}(a))(t\wedge \tau ) \end{aligned}$$

From definition of $\tau$, we know that

$$\begin{aligned} \log {a}\ge {\mathbb {E}}\log {I(t\wedge \tau )} \text { when } I_0\in (0,a] \end{aligned}$$

Hence, we have

$$\begin{aligned} {\mathbb {E}}(t\wedge \tau )\le \frac{\log {(\frac{a}{I_0})}}{L{\tilde{V}}(0)\wedge L{\tilde{V}}(a)} \end{aligned}$$

when $t\rightarrow \infty$

$$\begin{aligned} {\mathbb {E}}(\tau )\le \frac{\log {(\frac{a}{I_0})}}{L{\tilde{V}}(0)\wedge L{\tilde{V}}(a)}<\infty , \forall I_0 \in (0,a] \end{aligned}$$

Case 2 For all $t\ge 0$ and any $I_0\in (b,N)$, use (21) in (11), we have

$$\begin{aligned} {\mathbb {E}}\log {I(t\wedge \tau )}&={\mathbb {E}}\log {I_0}+{\mathbb {E}}\int _0^{t\wedge \tau } L{\tilde{V}}(I(s))\,{\mathrm {d}}s+0 \\&\le \log {I_0}+ {\mathbb {E}}(L{\tilde{V}}(b)\vee L{\tilde{V}}(N))(t\wedge \tau ) \end{aligned}$$

From definition of $\tau$, we know that

$$\begin{aligned} \log {b}\le {\mathbb {E}}\log {I(t\wedge \tau )} \text { when } I_0\in (b,N] \end{aligned}$$

Hence, we have

$$\begin{aligned} \log {b}\le & {} \log {I_0}+(L{\tilde{V}}(b)\vee L{\tilde{V}}(N)){\mathbb {E}}(t\wedge \tau ) \\ {\mathbb {E}}(t\wedge \tau )\le & {} -\frac{\log {(\frac{b}{I_0})}}{\mid (L{\tilde{V}}(b)\vee L{\tilde{V}}(N))\mid } \end{aligned}$$

when $t\rightarrow \infty$

$$\begin{aligned} {\mathbb {E}}(\tau )\le -\frac{\log {(\frac{b}{I_0})}}{\mid ({\tilde{LV}}(b)\vee {\tilde{LV}}(N))\mid }< \infty \ \ \forall I_0\in (b,N] \end{aligned}$$

Combine the results from both Case 1 and Case 2, and we complete the proof of Theorem 5.1. Now we need to give the mean and variance of the stationary distribution. $\square$

Theorem 5.2

If $R_0^S>1$ and m and v are denoted as the mean and variance of the stationary distribution of SDE model (5), then we have

$$\begin{aligned} \beta v=(\beta N-\mu -\gamma )m-\beta m^2 \end{aligned}$$

(22)

Proof

For any $I_0\in (0,N)$, we firstly recall (5) in the integral form

$$\begin{aligned} I(t)&= I_0+\int _0^t [\beta (N-I(s))I(s)-(\mu +\gamma )I(s)]\,{\mathrm {d}}s \\&\quad +\int _0^t [a_1 \sigma _1I(s)(N-I(s)) \\&\quad -a_2\sigma _2I(s)\sqrt{N-I(s)}]\,{\mathrm {d}}B_1(s) \\&\quad -\int _0^t a_3\sigma _2I(s)\sqrt{N-I(s)}\,{\mathrm {d}}B_2(s) \end{aligned}$$

Dividing both sides by t and when $t\rightarrow \infty$, applying the ergodic property of the stationary distribution [22] and also the large number theorem of martingales, we have the result that

$$\begin{aligned} 0=(\beta N-\mu -\gamma )m-\beta m_2 \end{aligned}$$

where $m,m_2$ are the mean and second moment of the stationary distribution. So we have

$$\begin{aligned}&0=(\beta N-\mu -\gamma )m-\beta (v+m^2) \\&\beta v=(\beta N-\mu -\gamma )m-\beta m^2 \end{aligned}$$

We have tried to get other equations of higher-order moment of I(t) in order to solve m and v but fail to get a result. Though we do not have an explicit formulae of mean and variance of stationary distribution like [10], simulations can still be effective to prove (22). $\square$

Fig. 7

Stationary: case 1

5.2 Simulation

In this section, we use the same values of our parameters in the last section

$$\begin{aligned}&N=100,\ \beta =0.5,\ \mu +\gamma =45,\\&\sigma _1=0.02,\ \sigma _2=0.05 \end{aligned}$$

and also two cases with different values of $\rho$

$$\begin{aligned}&a_1=1, a_2=0.7, a_3=1.6, \rho _1= 0.5>0, \\&R_0^S=1.0581944 \end{aligned}$$

and

$$\begin{aligned}&a_1=-0.1, a_2=0.5, a_3=0.8, \rho _2=-0.46<0, \\&R_0^S=1.108194 \end{aligned}$$

Now we simulate the path of I(t) for a long run of 200,000 iterations with step size 0.001 by using the Euler–Maruyama method [10, 16] in R. And we only reserve the last 10,000 iterations for the calculations. These 10,000 iterations can be considered as stationary in the long term, so the mean and variance of this sample are the mean and variance of the stationary distribution of our solution. In both cases, the results of left side and right side of the equation (22) are 10.84587 and 10.68102, 1.743753 and 1.848107, respectively, so we can conclude that the mean and variance of the stationary distribution satisfy Eq. (22). Figures 7 and 8 are the histograms and empirical cumulative distribution plots for each case of last 10000 iterations.

Fig. 8

Stationary: case 2

6 Conclusion

In this paper, we replaced independent Brownian motions in our previous model by correlated Brownian motions which leads to not only the increasing number of noises compared to Greenhalgh’s work [4, 10], but also turning the drifting coefficient into a nonlinear term. Then, we prove that the stochastic reproduction number $R_0^S$ is the Keynes to define the extinction and persistence of the solution. Similar to the deterministic SIS model, with $R_0^S<1$ and extra conditions, the disease will die out. When $R_0^S>1$, we prove that the solution will oscillate around a certain positive level. Compared to [10], our $L{\tilde{V}}$ is not linear, which results in more general and complicated conditions to both extinction and persistence sections. Moreover, compared to [23], this paper assumes that the Brownian motions are correlated, and hence, the effects of the correlations on the behaviours of our SIS system are studied. The analytical results including the form of $R_0^S$ and the additional restrictions indicate that the correlations between the Brownian motions do make a significant difference. Though we do not know the explicit expression of that level, numerical method are then used to find the exact value under certain circumstance. Moreover, when $R_0^S>1$, there is a unique stationary distribution of the solution. On the other hand, we have tried to get the explicit expression of the mean and variance by deducing higher moments of I(t), but we seems not able to get results at this time. Consequently, we will leave this as a future work.