Dynamic models of choice

Abstract

Parameter estimation in evidence-accumulation models of choice response times is demanding of both the data and the user. We outline how to fit evidence-accumulation models using the flexible, open-source, R-based Dynamic Models of Choice (DMC) software. DMC provides a hands-on introduction to the Bayesian implementation of two popular evidence-accumulation models: the diffusion decision model (DDM) and the linear ballistic accumulator (LBA). It enables individual and hierarchical estimation, as well as assessment of the quality of a model’s parameter estimates and descriptive accuracy. First, we introduce the basic concepts of Bayesian parameter estimation, guiding the reader through a simple DDM analysis. We then illustrate the challenges of fitting evidence-accumulation models using a set of LBA analyses. We emphasize best practices in modeling and discuss the importance of parameter- and model-recovery simulations, exploring the strengths and weaknesses of models in different experimental designs and parameter regions. We also demonstrate how DMC can be used to model complex cognitive processes, using as an example a race model of the stop-signal paradigm, which is used to measure inhibitory ability. We illustrate the flexibility of DMC by extending this model to account for mixtures of cognitive processes resulting from attention failures. We then guide the reader through the practical details of a Bayesian hierarchical analysis, from specifying priors to obtaining posterior distributions that encapsulate what has been learned from the data. Finally, we illustrate how the Bayesian approach leads to a quantitatively cumulative science, showing how to use posterior distributions to specify priors that can be used to inform the analysis of future experiments.

In this article, we describe how to fit cognitive models of the process of evidence accumulation, in which evidence favoring different options is accumulated over time until a threshold is reached that triggers an associated response. There are many advantages to the evidence-accumulation approach, such as its abilities to specify a comprehensive account of the probability of each choice and the associated distribution of times to make them, and to provide parameter estimates that quantify latent (i.e., not directly observable) quantities of psychological interest (e.g., the quality of the evidence provided by a choice stimulus and the amount required to trigger a choice). As a result, these models have been widely adopted, with the two most prominent variants, the diffusion decision model (DDM; Ratcliff & McKoon, 2008) and the linear ballistic accumulator (LBA; Brown & Heathcote, 2008) having been used in hundreds of articles with applications to a wide array of topics in animal cognition, psychology, and the neurosciences, including vision, attention, language, memory, cognition, emotion, development, aging, and clinical conditions, as well as applications in biology and economics (for reviews, see Mulder, van Maanen, & Forstmann, 2014; Ratcliff, Smith, Brown, & McKoon, 2016).

Unfortunately, parameter estimation in the context of evidence-accumulation models can be challenging. We discuss below why this leads us to prefer a Bayesian approach to parameter estimation, and we provide flexible open-source software for this purpose. The Dynamic Models of Choice (DMC; osf.io/pbwx8)¹ software is written in R (R Core Team, 2016) and is accompanied by a series of tutorials that guide the user through the process of inferring parameters from data, and that also provide advice based on our experience (see Table 1 for an overview).

Table 1 DMC tutorials

In the first part of the article, we provide a basic introduction to Bayesian estimation of the most longstanding evidence-accumulation model of choice and response times (RTs), the DDM. We then illustrate the challenges associated with fitting evidence-accumulation models to data using the LBA, which, although developed more recently, has found wide application due to its computational tractability. In this illustration we explain best practices in cognitive modeling, such as parameter- and model-recovery simulations that address these challenges. These practices can be adapted by users to explore the strengths and weaknesses of any of the many different types of evidence-accumulation models implemented in DMC in the specific context of the experimental design and parameter region relevant to their own research.

Evidence-accumulation models have transcended their roots in simple decision processes and have provided the building blocks for more wide-ranging cognitive models. In the second part of this article, we explore a complex contingent-choice task; in particular, we focus on a type of contingent choice in which participants are required to withhold their response upon detecting a signal that occasionally appears after the choice stimulus. Race architectures have long been applied to this “stop-signal” paradigm in order to provide nonparametric estimates of the ability to stop (i.e., inhibit) ongoing responses (Logan & Cowan, 1984; Logan, Cowan, & Davis, 1984). More recently, these models have also been used to provide parametric accounts of response inhibition (Logan, Van Zandt, Verbruggen, & Wagenmakers, 2014; Matzke, Dolan, Logan, Brown, & Wagenmakers, 2013a) and to model failures to attend to the stop signal (Matzke, Love, & Heathcote, 2017b).

We use an extension of a parametric stop-signal model, proposed by Matzke, Curley, Gong, and Heathcote (2018a), to illustrate the power and flexibility of DMC to model complex cognitive processes. We provide the mathematical details of Matzke et al. (2017a, b) model, both because the same types of equations underpin many evidence-accumulation models and because they illustrate how easy it is to extend these models to account for mixtures of processes caused, for instance, by attention failures. We illustrate the advantages of Bayesian hierarchical modeling by applying it to experimental stop-signal data, and then show how to use the resulting parameter estimates to quantitatively inform the analysis of future experiments.

Evidence-accumulation models

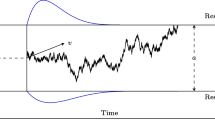
The most widely known exemplar of evidence-accumulation models, the DDM, is restricted to binary choice and assumes that evidence is continuous and stochastic (i.e., that it varies from moment to moment during accumulation). As is shown in Fig. 1, the DDM has four core parameters: drift rate (v), threshold (a), starting point (z), and nondecision time (t₀). The drift rate quantifies the mean rate of evidence accumulation, which can be influenced by individual differences in the quality of information processing and by stimulus characteristics related to task difficulty. Threshold quantifies the separation of the two response boundaries and reflects response caution; large values of a indicate that a large amount of evidence must be accumulated before a decision boundary is reached. The starting point parameter quantifies the initial evidence value before accumulation starts, reflecting participants’ a priori response bias. Nondecision time quantifies the duration of processes outside the decision-making process. The nondecision time is the sum of the time to encode the stimulus in a form suitable to provide evidence about the choice and the time to produce a response once the threshold is reached. The choice RT is the sum of the nondecision time, which is assumed to vary between trials uniformly over a range s_t, and the decision time, beginning when accumulation starts and ending when the threshold is first reached. The DDM also assumes uniform variability in the starting point from choice to choice over a range s_z, and Gaussian variability in the rate of evidence accumulation from choice to choice with standard deviation s_v; together, these account for the relative speeds of error and correct responses (Ratcliff & Rouder, 1998). To identify the model, the moment-to-moment variability of the accumulation rate is fixed to 1, consistent with the convention in the rtdists package (Singmann, Brown, Gretton, & Heathcote, 2017), used by DMC to compute the DDM distribution functions.²

Fig. 1

Schematic of a diffusion decision model. Evidence is on the ordinate, and time is on the abscissa. The stimulus is either s1, with corresponding response r1, or s2, with corresponding response r2. The inputs have a normal distribution with mean v and standard deviation sv≥0. The starting point for accumulation has a uniform distribution with mean z and width sz≥0, with the boundary for r1 located at zero and that for r2 at a > 0. The nondecision time is the sum of the encoding time (t_e) and the response production time (t_r), and is assumed to have a uniform distribution with mean t₀≥0 and width st. The figure depicts a case in which s2 is presented, the sampled evidence rate (depicted by an arrow) is correspondingly positive, and the sampled start point is unbiased (i.e., exactly halfway between the two boundaries). The actual path of evidence accumulation during a trial varies due to moment-to-moment noise and is depicted by a wavy line (note that in reality this path is usually much more jagged). For scaling purposes, the moment-to-moment variability in the accumulation rate (s) is fixed to 1. This figure is also available at https://tinyurl.com/y7h94ebp under a Creative Commons CC-BY license, https://creativecommons.org/licenses/by/2.0/

More general models of choice for two or more response options usually assume a race among (discrete or continuous) stochastic evidence-accumulation processes, with one runner per option. The choice is determined by the winner of the race (i.e., the first runner to reach its threshold). In simple linear versions, the runners race independently (e.g., Logan et al., 2014; Van Zandt, Colonius, & Proctor, 2000), whereas in more complex, nonlinear versions the runners interact cooperatively and/or competitively during evidence accumulation (e.g., Ratcliff & Smith, 2004; Usher & McClelland, 2001). Recently proposed deterministic race models, such as the LBA and the lognormal race (LNR; Heathcote & Love, 2012), keep some elements of choice-to-choice variability but drop the stochastic component. Their linear and independent trajectories during evidence accumulation make them more computationally and mathematically tractable than their predecessors. As is illustrated in Fig. 2, the LBA assumes that the accumulators corresponding to the different response options linearly accrue evidence with mean drift rate v and trial-to-trial variability s_v, commencing from start points drawn from independent uniform distributions from 0 to A for each accumulator. The first accumulator to reach its threshold (b) determines the response and decision time. As in the DDM, the RT is the sum of the decision time and the nondecision time (t₀).

Fig. 2

Schematic of a binary linear ballistic accumulator. Evidence is on the ordinate, and time is on the abscissa. The stimulus is either s1, with corresponding response r1, or s2, with corresponding response r2. Inputs have a truncated (positive) normal distribution with mean v, corresponding to the parameter mean_v in DMC, and standard deviation sv, corresponding to the parameter sd_v in DMC. The starting point for accumulation has a uniform distribution from 0 to A and threshold b, with B = b – A being the parameterization of the threshold used in DMC, making it easy to enforce the constraint that b > A by setting a prior, where B > 0. Prior constraints are also used to enforce sd_v > 0, whereas mean_v is unbounded. The nondecision time, the sum of the encoding time and response production time, corresponds to the t0 parameter in DMC. We usually bound t0 between 0.1 and 1 s. The figure depicts a case in which s2 is presented (i.e., the evidence rate distribution is more positive for the r2 accumulator than for the r1 accumulator), and the sampled rate for the r2 accumulator is greater than the sampled rate for the r1 accumulator (i.e., the dashed line depicting the accumulation path is steeper for r2 than for r1). However, the sampled starting point is higher for r1 than for r2, so the r1 accumulator reaches its threshold after time t_d and the response is an error with RT = t₀ + t_d. This figure is also available at https://tinyurl.com/ybpgwn84 under a Creative Commons CC-BY license, https://creativecommons.org/licenses/by/2.0/

In the past, applications of evidence-accumulation models have been largely restricted to rapid choices (typically faster than 1 s), but they are being increasingly applied to slower choices (e.g., Lerche & Voss, 2018; Palada et al., 2016) and to more complex cognitive processes. Race models, such as the LBA, implement winner-takes-all dynamics that can be used to build powerful and general-purpose computations (e.g., Maass, 2000; Šíma & Orponen, 2003). Models in which the racers are statistically independent are computationally and mathematically tractable, underpinning recent applications to complex choices contingent on logical relationships among the stimulus features (Eidels, Donkin, Brown, & Heathcote, 2010), to choices among complicated options in the multi-attribute LBA (Trueblood, Brown, & Heathcote, 2014), and to choices for which the evidence changes during the decision process (piecewise LBA; Holmes, Trueblood, & Heathcote, 2016). Independent race models can also be extended to account for mixtures of different types of responding, even in complex paradigms—enabling, for example, Bushmakin, Eidels, and Heathcote’s (2017) account of attention failures in a complex contingent-choice task.

DMC is designed to make it relatively easy for more advanced users to implement these and other advanced evidence-accumulation models (for an introductory “how to,” see tutorials 2.3 and 2.4, and for the range of such models already included in the standard distribution, see tutorials 5.1–5.6). However, in the main the tutorials focus on the DDM, LBA, and LNR. They provide a hands-on introduction that lets users explore these standard models (tutorials 1.3–1.5), and they show how to use Bayesian methods to fit the models to binary-choice data from a single participant (3.1–3.4) or from groups of participants (4.4–4.7).³ DMC also provides the functionality to simulate data from any DMC model (tutorials 1.2 and 4.1), consistent with a philosophy that encourages checking model implementations through simulating data and determining whether the data-generating parameters can be recovered through fits to the simulated data. In what follows, we first introduce the basic concepts of Bayesian parameter estimation and then apply these to fitting the DDM to a single participant’s data. We then use the LBA to illustrate parameter recovery and other good practices in cognitive modeling (Heathcote, Brown, & Wagenmakers, 2015). Finally, we illustrate how DMC can be used with an advanced model.

Bayesian parameter estimation

Bayesian estimation starts from prior distributions representing knowledge about the model parameters before the data are observed (tutorials 2.1, 2.2, and 4.2). The prior distributions are updated by the incoming data using Bayes’s rule: This results in the posterior distributions. Panel A of Fig. 3 illustrates the basic concepts of Bayesian parameter estimation using the nondecision time (t₀) parameter of the DDM for three fictitious participants. The gray dashed line shows the prior distribution. Here we assume a relatively noninformative normal distribution for each participant with mean 0.35 and standard deviation 0.25, truncated below at 0.1 s. The truncation reflects the prior assumption that choice RTs less than 0.1 s are implausible. The solid black lines show the posterior distributions. The central tendency of the posterior can be summarized using the mean, mode, or median of the distribution; these summary statistics are often used as point estimates for the parameters. The mean of the posterior distribution of the first participant is indicated by the vertical dotted line.

Fig. 3

Bayesian parameter estimation. (A) Prior (gray dashed line) and posterior (black solid lines) distributions; the crosses indicate the true data-generating parameter values; CI = credible interval. (B) Markov chain Monte Carlo (MCMC) chains. For each participant, each colored line (18 lines/participant) corresponds to one MCMC chain sampled from the posterior distribution; each chain comprises 200 converged posterior samples. This figure is also available at https://tinyurl.com/yalupk58 under a Creative Commons CC-BY license, https://creativecommons.org/licenses/by/2.0/

Bayesian inference, however, offers more than just point estimates: The posterior distributions quantify the uncertainty of the parameter estimates. In Fig. 3, the posteriors of the second and third participants are relatively narrow, whereas the posterior of the first participant is quite wide, indicating substantial uncertainty in estimating this parameter. The 95% credible interval (CI) of the posterior, indicated by the horizontal bar, summarizes the uncertainty of the estimate and quantifies the range within which the true data-generating parameter value (the gray cross) lies with 95% probability. The straightforward probabilistic interpretation of the Bayesian CI is in sharp contrast with the sometimes-nonsensical nature of the nominally analogous frequentist confidence interval (for a pointed commentary, see Morey, Hoekstra, Rouder, Lee, & Wagenmakers, 2016). For more detailed introductions to Bayesian methods, the reader is referred to Edwards, Lindman, and Savage (1963), Gelman et al. (2013), Kruschke (2010), and Wagenmakers et al. (2018).

For complex models, such as the DDM and the LBA, the posterior distribution cannot be derived analytically. Rather, the it must be approximated by drawing sequences of samples—chains—using Markov chain Monte Carlo (MCMC) methods (Gamerman & Lopes, 2006; Gilks, Richardson, & Spiegelhalter, 1996). This is illustrated in Panel B of Fig. 3, which shows, for each participant, 18 MCMC chains (by default, DMC uses three times as many chains as parameters, which is six in this case), each comprising 200 samples from the posterior distribution. MCMC sampling in the context of evidence-accumulation models can be challenging. For instance, in race models such as the LBA, we observe the outcomes associated with the winner (responding at a certain time) but only get indirect knowledge about the loser (that it was slower). As a result, such models are “sloppy”—a pervasive phenomenon in models of biological systems (Gutenkunst et al., 2007)—meaning that their parameters can be highly correlated. Sloppiness causes most standard MCMC samplers to be grossly inefficient. DMC uses the Differential-Evolution sampler (DE-MCMC; Turner, Sederberg, Brown, & Steyvers, 2013), which avoids this problem by using a large set of MCMC chains. The values in different chains are compared in a “crossover” step that provides information about correlations, which then guides the sampler’s exploration of the parameter space (ter Braak, 2006, p. 240).

As sampling progresses, the influence of the data grows until an equilibrium is reached so that the proper “posterior” (i.e., after the data have had their full influence) samples are being obtained. The initial “burn-in” samples are discarded, and additional “converged” samples are obtained that are sufficient to reliably estimate statistics that characterize the posterior distributions. For example, sample means may be used to characterize the central tendency of the posteriors. Similarly, the span between the smallest and largest 2.5% of the samples may be used to compute CIs.

DMC tutorials for the DDM, LBA, and LNR focus on the process of using DE-MCMC to obtain converged samples that adequately approximate the posterior distributions and the associated uncertainty of the parameter estimates. Obtaining and verifying convergence can require judgment and is best confirmed by (1) assessing the similarity of within- and between-chain variability (“mixing”) using Brooks and Gelman’s (1998) $\widehat{R}$ statistic, and (2) visually checking that the MCMC chains have the appearance of “flat fat hairy caterpillars,” in which most samples are in the middle, with occasional spikes, and that there are no systematic upward or downward tendencies (tutorials 3.1 and 3.2). This last condition can be difficult to assess, because converged chains may still have slow oscillations, reflecting long-time-scale correlations across sequences of samples. In such cases, it is useful to “thin” the chains, keeping only, say, every 10th or 20th sample, which also makes the samples less redundant and the corresponding recorded samples of a more manageable size.

DMC facilitates the process of assesing convergence by building on functions from the R base and the CODA package (Plummer, Best, Cowles, & Vines, 2006) to quantify redundancy (autocorrelation) and the effective number of independent samples⁴ and to calculate $\widehat{R}$ and plot the chains (see tutorial 3.2), as well as to determine an appropriate level of thinning (tutorial 4.6). DMC also provides a tweak of CODA that enables users to superimpose the posterior distributions over the prior distribution. This alerts users to cases in which the estimates reflect the prior more than the posterior (i.e., the data have not “updated” the prior), which can be a problem, at least when the prior is uninformative, in particular experimental designs for parameters that are only weakly constrained by the data.

Fitting the diffusion decision model

Here we illustrate the basic concepts of Bayesian parameter estimation by guiding the reader through tutorial 3.4, which demonstrates fitting a six-parameter DDM to simulated data for a single participant. As is depicted in Fig. 4 (drawn with the plot.cell.density function), the design is minimal and the data set large, with 10,000 decisions to each of two equally frequent stimuli. As is shown by the “profile” plots in Fig. 5a (drawn with the profile.dmc function), the large sample size means that the most likely parameters for the data correspond quite closely to the generating values (see the Fig. 5 caption for details). Sampling was carried out with the prior distributions shown in Fig. 5b (drawn with the plot.prior function), which are noninformative because they spread their probability mass over a wide range around the true values, and so have little influence on the sampling.

Fig. 4

Correct (black) and error (red) response time distributions simulated from the DDM for two stimuli s1 and s2, each with 10,000 responses (drawn with the plot.cell.density function)

Fig. 5

(a) Profile plots (drawn with the profile.dmc function) of the likelihood of each parameter of the DDM in a range around its true value, with all other parameters fixed at their true value. The true values (with the peak of each likelihood in brackets) are a = 1 (1.0), v = 1 (0.97), z = 0.50 (0.50), sv = 1 (1.04), sz = 0.2 (0.24), and t₀ = 0.15 (0.15). (b) Prior distributions (drawn with the plot.prior function)

First, we ran 400 iterations (using the run.dmc function) for each of the 18 (3 × 6) MCMC chains. Initial values were randomly drawn from the prior (using the samples.dmc function); thus, they are often far away from the true values and so have very small likelihoods. The left panel of Fig. 6 shows that as sampling progressed, posterior log-likelihoods rapidly increased, and Fig. 7a shows that the posterior samples for the parameters rapidly converged on the generating values. The middle panels of Figs. 6 and 7b zoom in on the last 100 iterations, showing that the chains are already quite flat, with the posterior log-likelihood having, as expected, a negatively skewed distribution, and the posterior samples varying fairly symmetrically. The initial 400 iterations augmented the core crossover step with a 5% probability of taking “migration” steps (Turner et al., 2013, pp. 383–384) that replace low-likelihood chains with slightly perturbed copies of higher-likelihood chains. Migration deals with chains that become stuck in low-probability areas of the parameter space. The right panel of Fig. 6 illustrates this “stuck chain” phenomenon during the last 200 iterations of a fresh run of 400 iterations commencing from randomly generated start values when migration is turned off. One chain does not move toward the posterior mode as rapidly as the others. In extreme cases, such chains can remain stuck for a very long time, greatly slowing convergence. In general, migration is very useful during burn-in because it drives the sampler in the right region of the parameter space, but if it is used extensively it can lead to false convergence (i.e., all chains converge on the same suboptimal solution); in our experience, this does not occur if migration is only allowed on 5% of the iterations.

Fig. 6

Posterior log-likelihoods (drawn with the plot.dmc function) for the first 400 iterations (left panel), posterior log-likelihoods for the last 100 iterations (i.e., the first 300 iterations are removed; middle panel), and posterior log-likelihoods for the last 200 out of 400 iterations when migration is turned off (right panel). Note that the x-axis is drawn from 0 in each case

Fig. 7

(a) Markov chain Monte Carlo (MCMC) chains comprising the first 400 iterations (drawn with the plot.dmc function). (b) MCMC chains comprising the last 100 out of 400 iterations. (c) MCMC chains comprising the final 1,000 iterations, for which the posterior medians (with 95% credible intervals in brackets) were a = 1.01 (0.99–1.03), v = 1.03 (0.95–1.10), z = 0.499 (0.495–0.503), sv = 1.06 (0.83–1.29), sz = 0.28 (0.10–0.36), and t₀ = 0.151 (0.147–0.154)

The results obtained with migration steps cannot be used for inference, since they tend to bias the posterior samples to higher-likelihood regions. Therefore, we turned off migration after the initial set of 400 iterations and obtained a fresh set of 500 samples. Visual inspection of the chains, using the same plot.dmc function used to generate the plots in Fig. 7, revealed the required flat, fat, hairy caterpillars, but the $\widehat{R}$ values (assessed with the gelman.diag.dmc function) were still a little above the recommended cutoff (at least less than 1.2, and ideally less than 1.1), and the effective sample size, which adjusts the actual sample size (18 chains × 500 iterations) for redundancy due to autocorrelations (assessed with the effectiveSize.dmc function) was only around 300. After another 500 iterations were added, the chains passed visual inspection (Fig. 7c), the $\widehat{R}$ values were less than 1.1, and the effective sample sizes were greater than 500 except for trial-to-trial variability in start point (sz), for which $\widehat{R}$ was a little higher (1.14) and the effective sample size a little less than 500. However, as is detailed in the caption of Fig. 7, these posterior samples already provide quite good approximations of the posterior distributions, with posterior medians quite close to the true values, which also fall within the estimated 95% CIs. In the tutorial, further samples are taken to improve the sampling of sz, which is often the most difficult DDM parameter to estimate. The tutorial also illustrates the assessment of the goodness of fit of the model and checks on the level of autocorrelation, but we leave these details for users to explore when working through tutorial 3.4 and the other tutorials provided with DMC. To guide that exploration, Table 1 provides an overview of the DMC tutorials. An expanded version of this table, supplied with DMC’s readme file, identifies the tutorial that introduces each of DMC’s functions.

Challenges and solutions in model fitting

Having discussed a relatively simple example, in this section we guide the reader through a set of LBA analyses of simulated binary-choice data that illustrates why parameter estimation can be challenging. We also show how to apply methods such as parameter-recovery studies (e.g., Heathcote et al., 2015) in order to investigate whether parameter estimates are meaningful. Some examples examine the asymptotic behavior of the LBA in large simulated data sets, and others show how to check its behavior in designs representative of real experiments by examining fits to multiple small simulated data sets. The tutorial associated with the analyses (DMCpaper1.R, available with the tutorials in the OSF distribution) enables readers to work through the example analyses.

Parameter correlations and model identification

As a result of the sloppiness of evidence-accumulation models, and the associated parameter trade-offs, estimates can be very uncertain, making it difficult to identify the values that generated the data. In the extreme case of perfect correlation, parameters are nonidentified. That is, their estimated values are meaningless because the effects of changing one parameter can be exactly compensated for by changing another, meaning that parameter values have no explanatory value. To illustrate, consider evidence-accumulator models in which decision time (t_d) equals the distance that has to be traveled from start point to threshold (D) divided by the rate of accumulation (v): t_d = D/v. It is easy to see that a change in D (e.g., doubling) has no effect on t_d if an appropriate adjustment is made to v (e.g., also doubling).

Example 1.0 in DMCpaper1.R shows that DE-MCMC is able to obtain convergence even in the completely nonidentified LBA, but that it produces parameters that are inaccurate, uncertain, and strongly correlated. Fortunately, MCMC methods naturally alert users to problems with parameter estimation. In particular, as is illustrated in Fig. 8a, it is straightforward to plot pairs of posterior samples against each other to assess the degree of correlation between the parameter estimates. As is shown in Example 1.1, the identification issue is conventionally addressed by fixing the trial-to-trial standard deviation of the accumulation rate (sd_v) to 1,⁵ which produces accurate and precise estimates for exactly the same simulated data, as is illustrated in Fig. 8b. The data were simulated with sd_v = 1, but this is shown not to matter in Example 1.2, in which the same good performance is obtained by fixing sd_v = 2, with the only difference being that the parameter estimates (except for nondecision time) double.

Fig. 8

Pair plots of the parameter estimates from a large data sample (20,000 trials). The main diagonal shows histograms of the 2,700 posterior samples; the lower triangle shows scatterplots between the posterior samples; and the upper triangle reports correlations for the corresponding panel in the lower triangle (reflected over the main diagonal). (a) Example 1.0: Nonidentified LBA with all parameters estimated. (b) Example 1.1: Conventional-identified LBA with the restriction sd_v = 1

Figure 8b shows that even when sd_v is fixed to 1, the correlation between nondecision time (t₀) and the threshold parameter (B) remains large (i.e., – .995). Example 1.3a fixes B instead and shows that this produces generally worse performance and higher posterior correlations, because B does not entirely determine the distance to threshold, with the start-point noise (A) also playing a role. Examples 1.3b and 1.3c show that fixing the mean rates generally does as well as or better than fixing sd_v, whereas Example 1.3d shows that fixing start-point noise (A) does markedly worse than all other cases. Note that although large correlations can make parameter estimation difficult, they are a natural part of sloppy models and do not necessarily indicate that there is a fatal problem with the model specification.

Overall, it is clear that fixing a rate-related parameter is to be preferred, but it must be kept in mind when interpreting the results that if one parameter is fixed (e.g., sd_v), an apparent effect on other parameters might really be due to a change in the fixed parameter. Note also that when there is more than one accumulator parameter of a particular type, only one needs to be fixed in order to identify the model. As an illustration, Example 1.4 simulates data from a model in which sd_v is twice as large for the accumulator that does not match the stimulus, denoted sd_v.false, as for the accumulator that matches the stimulus, denoted sd_v.true, with only sd_v.false being fixed; the model’s ability to recover the data-generating parameter values remains excellent.

Parameter-recovery study

Often, researchers use evidence-accumulation models because they are interested in whether the model parameters vary over some manipulation—for example, whether the mean accumulation rates vary between two conditions. Answering such a question requires a “measurement model”—that is, a model that can reliably identify the processes that generated the data. This can be tested with a “parameter-recovery study” (e.g., Heathcote et al., 2015). Parameter recovery involves simulating data from known parameter values, fitting the model to the synthetic data as if they had been obtained from a real experiment, and then determining whether the estimated parameters match the true data-generating parameters. DMC provides a set of functions to facilitate parameter-recovery studies, described using the example below.

Because the model in Example 1.4 is commonly found to hold in real data, we use it to illustrate a small-sample (100 trials for each stimulus) parameter-recovery study in Example 1.5. We fit 200 replicated data sets generated with identical parameter values, which is made simple by DMC’s ability to simulate and fit any number of subjects with a single command (although the computational time can become substantial).

Given the large number of data sets, visual convergence diagnostics are impractical. Fortunately, the RUN.dmc function is specifically designed for parameter-recovery studies and addresses convergence problems automatically. It augments crossover steps with a migration step until stuck chains are removed, then turns off migration and adds new samples and removes old samples until chains are mixed (checked with $\widehat{R}$) and flat (checked by comparing the location and spread of the first and last third of the samples). RUN.dmc performs all checks repeatedly, starting with stuck chains then moving on to mixing and flatness, but going back to stuck chains if necessary until convergence is reached and, if requested, a minimum number of posterior samples are obtained.

In parameter-recovery studies, the mean of the posterior medians and 95% CIs across replications can provide an indication of the average performance of the model, as is shown in Table 2. Bias, measured by the difference between the posterior median and the true value, is negligible (1%–5%) and very similar to that in the large-sample result. With increased sample size, the precision of the 95% CIs increases (i.e., the CIs get narrower). The gain in precision from the 100-fold increase in sample size in Example 1.4 relative to Example 1.5 (20,000 vs. 200 trials) varies from close to a square-root law (~ 10 = $\sqrt{20000/200}$), as is generally found for simple linear models, to about half that value. The final row of Table 2 reports the “coverage” of the 95% CIs, computed as the percentage of times across the 200 replications that the true value fell within the 95% CI. The precision of the coverage estimates relies solely on the number of replications, so with only 200 replications it is relatively coarse. Nevertheless, the results suggest that coverage is good (i.e., close to the nominal value of 95%).

Table 2 Results of a parameter-recovery study with fits to 200 data sets of 200 observations each (100 for each of two stimuli) generated using the parameter values given in the “True” row, resulting in approximately 25% errors (Example 1.5)

Figure 9a shows the prior distributions for Examples 1.4 and 1.5. Figure 9b and c contrast the updating brought about by, respectively, the large data sample in Example 1.4 and the small data sample for a single replicate in Example 1.5. In the large-sample case, the prior is completely dominated, whereas in the small-sample case, updating is more moderate. However, even in the latter case, the influence of the prior is still largely negligible, as is appropriate, given that the priors were relatively uninformative.

Fig. 9

Priors and posteriors for the linear ballistic accumulator in Examples 1.4 and 1.5. (a) Prior distributions. (b) Prior (red lines) and posterior (black peaked lines) distributions for Example 1.4 with a large data sample (20,000 trials). (c) Prior and posterior distributions for one replicate from Example 1.5 with a small data sample (200 trials). For the large data sample (b), the posterior density is much more concentrated than the prior density, and thus the priors appear very flat relative to the posteriors. This suggests that the priors had minimal influence on the posterior distributions. For the smaller data sample (c), the posterior density is more similar to the prior, but still fairly well updated

The importance of making mistakes

Sufficient trials per participant is not the only prerequisite for good parameter estimation in evidence-accumulation models; participants also need to make a sufficient number of errors. To illustrate this, we first look at the extreme case of perfect accuracy by fitting models that take this fact into account, as would be the case when modeling detection performance (i.e., making a single response to the onset of a stimulus) by assuming only a single evidence-accumulation process. We show that asymptotic performance is similar to the choice cases addressed previously with 25% errors, both in Example 1.6 for the LBA and in Example 1.7 for the LATER model (Carpenter, 1981), a simplification of the LBA with start-point noise fixed at 0, which is often used in detection paradigms.

In contrast, when the error rate is low but nonzero (~ 2.5%) and the full model from Example 1.4 is fit, recovery can be poor. Example 1.8 examines the asymptotic case. Although the parameter estimates are not biased, the posterior uncertainty can be very large, with the width of the 95% CIs ranging from 10% of the parameter values (for B and t₀) through more than 100% of the values (for sd_v.true). Example 1.9 outlines a parameter-recovery study like Example 1.5, with results reported in Table 3. Bias is much larger, and the inflation in uncertainty is similar to that in the asymptotic case. This illustrates that parameter recovery depends on the region of the data-generating parameter space. In practice, we find it is useful to explore the parameter region using data from pilot subjects, then to use the obtained parameter estimates to simulate data sets with different numbers of trials in order to guide the design of experiments.

Table 3 Results of the parameter-recovery study with fits to 200 data sets of 200 observations each (100 for each of two stimuli) generated using the parameter values given in the “True” row, resulting in approximately 2.5% errors (Example 1.9)

Generally, when fitting choice models, it is best to have reasonably high error rates. When high-accuracy performance is of interest, it is beneficial to add a within-subjects manipulation to the design that also produces a lower accuracy condition. This is illustrated in Example 1.10, a small-sample parameter-recovery study with an extra factor that combines Examples 1.5 and 1.9 in order to produce high (~ 25%) and low (~ 2.5%) error conditions, while keeping the total number of trials per replication constant (50 trials in each cell of the 2×2 design, so 200 trials in total). The results indicate similar levels of uncertainty in the high-error condition and the pure high-error case in Example 1.5. The low-error condition, however, results in much smaller uncertainty than in the pure low-error case in Example 1.9 (~ 10%–60%), indicating a substantial gain favoring the design that manipulates accuracy.

Comparing parameters and models

In the previous example, accuracy was manipulated by keeping the matching rates constant, but making the mismatching rate much higher for the low- than for the high-accuracy condition. We use this setup to illustrate how to test differences in parameters. This is done by computing the posterior distribution of the difference between parameters by calculating pairwise differences between samples from the joint posterior. Bayesian p values can be computed from the probability that one parameter is greater than another by tallying the number of times the differences are greater than 0 (tutorial 5.6 describes how to test arbitrary functions of parameters). We show that the test is well-calibrated in the case of the null difference between matching rates, since the p values from the 200 replications are approximately uniformly distributed between 0 and 1 (however, this is not always the case; see Gelman, 2013). For the mismatching rate, in contrast, even the smallest p value is greater than .995, indicating that this difference is easily detected.

Model selection “information criteria,” such as the DIC (Spiegelhalter, Best, Carlin, & Van Der Linde, 2002), BPIC (Ando, 2011), and WAIC (Watanabe, 2010), provide another way of testing, for instance, whether the matching rates are different. The model in Example 1.10 is more complex than is needed, in that it estimates the two matching rates separately, even though their true values are identical. In Example 1.11, we fit to the same 200 data sets used in Example 1.10 to a simpler model that removes this redundancy and so requires one less estimated parameter. The information criteria reward goodness of fit but penalize redundancy, so if well-calibrated, they should detect that the matching rates are not different and select the simpler model. Note that this is a difficult problem, because both models are in a sense correct, and the more complex model must fit the data at least as well, and probably a little better, than the simpler model, since it can soak up some variation due to noise.

We used a model-recovery study to investigate whether the information criteria can indeed recover the data-generating simpler model. When summed over data sets, DIC and WAIC clearly prefer the simpler model by about the same margin, whereas for BPIC the preference was even stronger. However, when tallying the proportion of individual data sets in which the simpler model was selected, WAIC did surprisingly poorly, barely scoring over 65%, whereas for DIC this percentage was 77%, and for BPIC it was 83%. These results are surprising, given the increasing popularity of WAIC over the standard DIC approach (Gelman et al., 2013) and the relative obscurity of BPIC. The results also illustrate the utility of using model-recovery studies to check the performance of model-selection criteria, particularly in situations with relatively few trials per participant (tutorial 3.5 provides more details on model selection).

Stop-signal race model

Stop-signal race models assume a statistically independent race between a “go” (i.e., choice) runner and a “stop” runner. If the stop runner wins, the choice response is inhibited, but if the go runner wins, the response is executed. In the stop-signal paradigm, the problem of partial observation becomes worse. This is because the finishing times of the stop runner cannot be directly observed; they must be inferred from how the difference in onset between the choice stimulus and the stop signal (stop-signal delay; SSD) changes the RT distribution of failures to stop relative to the distribution of choice RTs on trials without stop signal (Matzke, Verbruggen, & Logan, 2018b). Assuming “context independence” (i.e., that the choice runner is the same on trials with and without a stop signal), we can obtain a nonparametric estimate of the average time for the stop process to complete (stop-signal RT). The estimate is nonparametric because the model does not make assumptions about the parametric form of the distribution of finishing times for the runners (Logan & Cowan, 1984).

Parametric race model

Matzke et al. (2013a) advocated an alternative parametric Bayesian approach, which provides estimates of the full distribution of stopping latencies based on the assumption that the finishing time distributions of the runners follow an ex-Gaussian distribution (see Fig. 10). The ex-Gaussian is the sum of a normal distribution, with mean μ and standard deviation σ, and an exponential distribution, with mean τ, and has been widely used to describe RT distributions (e.g., Andrews & Heathcote, 2001; Heathcote, Popiel, & Mewhort, 1991; Matzke & Wagenmakers, 2009). Estimation of the race model requires the probability density function, f(t | θ) (i.e., the instantaneous probability of a runner finishing at time t), and the survivor function, S(t | θ) (i.e., the probability that a runner is still racing at time t), both of which are easily computed for the ex-Gaussian with parameter vector θ = (μ, σ, τ).

Fig. 10

The two-racer ex-Gaussian stop-signal race model. This figure is also available at https://tinyurl.com/ydezqk3p under a Creative Commons CC-BY license, https://creativecommons.org/licenses/by/2.0/

In a two-runner race, the likelihood that the go runner finishes at time t and the stop runner has not yet finished (i.e., the go runner wins at t) is L_GO(t) = f(t | θ_GO) S(t–SSD | θ_STOP).⁶ If the stop runner wins, the finishing time cannot be observed, so the likelihood of winning at each possible time point must be integrated (summed) in order to obtain the probability of stopping: ${p}_{STOP}=\underset{-\infty }{\overset{\infty }{\int }}f\left(t- SSD|\kern0.5em {\theta}_{STOP}\right)S\left(t|\kern0.5em {\theta}_{GO}\right) dt$. The integral must be evaluated numerically, which is slow, but it only needs to be done once for each SSD. Matzke, Love, Wiecki, et al. (2013b) provided software to fit a Bayesian implementation of this two-runner model.

Accounting for attention failures

DMC implements the two-racer ex-Gaussian model with an extension developed by Matzke, Love, and Heathcote (2017b) that incorporates attention failures in which the stop runner never gets off the blocks (tutorial 6.4). Matzke, Hughes, Badcock, Michie, and Heathcote (2017a) found that such “trigger failures” are common in schizophrenia patients, but they are also present in healthy controls. Estimation of the probability of trigger failures (p_tf) requires a straightforward extension to the likelihood. If the go runner wins, with probability p_tf only the go runner is active (i.e., there is no race), and otherwise the usual race occurs: L_GO(t) = p_tff(t | θ_GO) + (1 – p_tf) f(t | θ_GO) S(t–SSD | θ_STOP). Stopping cannot co-occur with trigger failures, so p_STOP is as before, but is less likely in proportion to the rate of trigger failures: ${p}_{STOP}=\left(1-{p}_{tf}\right)\underset{-\infty }{\overset{\infty }{\int }}f\left(t- SSD|\kern0.5em {\theta}_{STOP}\right)S\left(t|\kern0.5em {\theta}_{GO}\right) dt$. Matzke et al. (2017a, b) added the possibility of attention failures resulting from “go failures,” in which the go runner never gets off the blocks with probability p_gf (tutorials 6.1 and 6.2 outline similar extensions to standard evidence-accumulation models). Since go responses cannot co-occur with go failures, L_GO(t) = (1 – p_gf) [p_tff(t | θ_GO) + (1 – p_tf) f(t | θ_GO) S(t–SSD | θ_STOP)]. Since go failures must cause successful stopping: ${p}_{STOP}={p}_{gf}+\left(1-{p}_{gf}\right)\left[\left(1-{p}_{tf}\right)\underset{-\infty }{\overset{\infty }{\int }}f\left(t- SSD|\kern0.5em {\theta}_{STOP}\right)S\left(t|\kern0.5em {\theta}_{GO}\right) dt\right]$.

Accounting for choice errors

Paradoxically, the standard stop-signal paradigm relies on a choice task, yet the standard stop-signal model assumes a single go runner, and so cannot naturally accommodate choice errors. A detection task (i.e., a nonchoice task, such as responding to the onset of a stimulus) accords with the standard model’s assumption of a single go racer, but it is not used in practice, in order to avoid anticipatory responses. To minimize error rate, the stop-signal paradigm typically uses a very easy choice task and emphasizes accurate responding. In the ex-Gaussian stop-signal model, choice errors are regarded as contamination and are typically discarded. However, Matzke et al. (2017a, b) found that even with very low error rates (~ 2.5%), this approach can bias the parameter estimates, particularly when errors are slower than correct responses, which is usually the case when response accuracy is emphasized.

To address this limitation, Matzke et al. (2017a, b) proposed the “EXG3” model, which accounts for choice using a race between two ex-Gaussian go runners (one for each choice), along with one ex-Gaussian stop runner. The extension of the likelihood for go Choice 1 requires the inclusion of the survivor function for the Choice 2 runner not having finished: L_GO,1(t) = f(t | θ_GO,1) S(t | θ_GO,2) S(t–SSD | θ_STOP), and similarly for Choice 2. The probability of stopping is given by ${p}_{STOP}=\underset{-\infty }{\overset{\infty }{\int }}f\left(t- SSD|\kern0.5em {\theta}_{STOP}\right)S\left(t|\kern0.5em {\theta}_{GO,1}\right)S\left(t|\kern0.5em {\theta}_{GO,2}\right) dt$. DMC provides a Bayesian hierarchical implementation of the EXG3 model including the mixture extensions introduced above (tutorial 6.5).

Bayesian hierarchical parameter estimation

Bayesian hierarchical methods (e.g., Farrell & Ludwig, 2008; Gelman & Hill, 2007; Rouder, Lu, Speckman, Sun, & Jiang, 2005; Shiffrin, Lee, Kim, & Wagenmakers, 2008) simultaneously model data from a set of participants, assuming that their parameters come from the same population distribution (see tutorials 4.2 and 4.3). The population distribution describes how the parameters of the individual participants vary in the population. Figure 11 illustrates the basic concepts of hierarchical estimation using the μ_STOP parameter of the EXG3 model for three fictitious participants. Panel A shows that the participant-level parameters are drawn from a normal population distribution, truncated below at 0 (as all have units of time) and above at 4 s (to avoid potential numerical errors when large values are sampled). The population distribution is characterized by the population mean μ_μSTOP and the population standard deviation σ_μSTOP parameters. The population-level parameters are assumed to be unknown. This implies that we set priors (i.e., hyper-priors) on these parameters, which allows us to estimate them from the data. For the population mean, we specify broad truncated normal hyper-priors with a mean of .5 and a standard deviation of 1. For the population standard deviation, we choose an exponential distribution, reflecting the prior belief that smaller population standard deviations are more likely than large ones, with nonnegligible mass out to 4 s. The population-level parameters provide inference on the group level, whereas the participant-level parameters provide inference on the individual level.

Fig. 11

Bayesian hierarchical estimation. (A) Participant-level posteriors and the population distribution from the hierarchical analysis; crosses indicate the true data-generating parameter values; CI = credible interval. (B) Participant-level posteriors from the standard individual analysis; the gray dashed line indicates the prior distribution. In the individual estimations, the μ_STOP estimate of the first participant is well away from the rest of the group and is estimated imprecisely, as indicated by the relatively wide 95% CI. In hierarchical estimation, the population distribution pulls all three estimates toward the group mean. This “shrinkage” is greatest for the outlying first participant, but to a lesser degree also affects the estimates for the other two participants. As a result, the hierarchical estimates are less variable, more precise, and, on average, more accurate. This figure is also available at https://tinyurl.com/ydgwr7ox under a Creative Commons CC-BY license, https://creativecommons.org/licenses/by/2.0/

Hierarchical modeling uses information from the entire group, captured by the population-level parameters, to improve parameter estimation at the individual level. This is achieved by using the population distribution as a prior for the participant-level parameters. Even though the hyper-priors on the population-level parameters are largely noninformative, the prior on the participant-level parameters inferred by the hierarchical model can be quite informative. This occurs during the course of sampling, with each participant’s data tuning the population-level parameters, and the population distribution then providing a more and more informative prior for the participant-level parameters. As is illustrated in Fig. 11, this process alters the participant-level estimates from the hierarchical analysis (panel A) relative to the estimates from the standard individual analysis (panel B), “shrinking” them toward the group mean. The hierarchical estimates are therefore less variable, more precise (i.e., have narrower CIs), and, on average, more accurate than the estimates obtained from the individual analysis. The effects of shrinkage in the figure are most pronounced for the first participant, whose parameter is estimated with relatively large uncertainty.

Hierarchical estimation is especially valuable when the number of trials available for each participant is limited, because it garners some of the stabilizing effects of averaging while avoiding gross distortions from fitting nonlinear models to averaged data (e.g., Brown & Heathcote, 2003; Heathcote, Brown, & Mewhort, 2000). Because stop-signal trials—which provide most of the constraint on the stop parameters—typically constitute only a minority of the trials, hierarchical methods can greatly improve the quality of the parameter estimates associated with the stop runner.

Fitting empirical stop-signal data

We fit the EXG3 model hierarchically to the data from 47 participants⁷ in a stop-signal experiment that manipulated choice difficulty, resulting in ~ 12.5% errors in the easy and ~ 25% errors in the hard condition. The model featured 17 parameters, three parameters for each of the five ex-Gaussian distributions—one for stopping and four for the factorial combination of easy versus hard and match (i.e., “true”) versus mismatch (i.e., “false”) runners—and one each for go and trigger failures. The tutorial associated with this application (DMCpaper2.R) enables readers to work through the example analyses.

After a preliminary descriptive analysis, we first fit each participant’s data individually, using the methods described earlier and vague priors closely resembling those in Fig. 12a. This step provided start values for hierarchical sampling, since it can otherwise be difficult to find parameters that result in a valid likelihood, and because even if such estimates can be found, this two-step approach is usually much faster (tutorial 4.6). Moreover, the results from the initial stage can also be used to examine the validity of the population model; for instance, if participants cluster into groups, it is inappropriate to assume a common normal population distribution.

Fig. 12

Priors and posteriors for the EXG3 model. (a) Hyper-prior distributions for the population mean (location) parameters; similar priors were used in the individual fits for obtaining the start values for the hierarchical analysis. The common exponential prior for the population standard deviations (scale) is shown in the bottom right panel. (b) Hyper-prior (red lines) and posterior (black peaked lines) distributions for the population means. (c) Hyper-prior and posterior distributions for the population standard deviations. For both the population means (b) and the population standard deviations (c), the posterior distributions of all parameters except for tau.easy.false and tau.hard.false have shifted greatly from the priors. Hence, the posterior densities look relatively peaked as compared to the prior densities, which look relatively flat

From priors to posteriors

We assumed truncated normal population distributions for all model parameters. The hierarchical analysis requires two sets of hyper-priors, one for the mean (location) and one for the standard deviation (scale) of the population distributions (Fig. 12a). For the population means, we specified broad normal hyper-prior distributions truncated below at 0 and above at 4 s. For the μ parameters (both go and stop), we set the mean of the hyper-priors to 0.5 s and the standard deviation to 1. For σ and τ, we set the mean to 0.1 s and the standard deviation to 1. These settings produced broad and fairly noninformative priors with nonnegligible mass out to 3 s. The mixture proportion parameters (p_tf and p_gf) were transformed from the probability scale to the entire real line using a probit transformation and were assigned normal hyper-priors with a mean of -1.5 (~ 6.7% failure rate) and standard deviation of 1, giving broad priors with nonnegligible mass from – 4 (~ 0.003%) to 1 (~ 84%). For the population standard deviations, we chose identical exponential distributions for all parameters.

Figure 12b shows the hyper-prior and posterior distributions of the population means resulting from hierarchical estimation of the EXG3 model. Updating from prior to posterior was substantial for all but the two τ mismatch parameters. Since only slow finishing times are determined by the τ mismatch parameters, they are often poorly constrained. In parameter-recovery studies, Matzke et al. (2018) found that this weak identification does not spread to the other parameters; it remains beneficial to model the mismatching process in order to avoid the systematic biases produced by fitting a two-racer model that discards errors. Figure 12c shows the hyper-prior and posterior distributions of the population standard deviations, which measure individual differences. They are all well updated, again with the exception of the two τ mismatch parameters.

Goodness of fit

A crucial part of evaluating a model is checking whether it provides an adequate description of the observed data. To do so, we first simulate data from the model in a way that reflects our uncertainty about its parameters by mixing together data simulated from random samples from the joint posterior distribution. Just as in the observed data, these “posterior-predictive” data can be aggregated to produce summary statistics and plots. From a Bayesian perspective, there is uncertainty about the model predictions resulting from sampling variability and posterior uncertainty, but there is no uncertainty about the data (“the data are the data”). Figure 13 provides goodness-of-fit plots, averaged over participants and posterior samples applicable to most choice paradigms, whereas Fig. 14 provides plots specific to the stop-signal paradigm, showing goodness of fit as a function of SSD. The figures show average results over participants, which is useful as a summary and also for detecting systematic misfit, which is often difficult to see at the individual level (DMC also provides goodness-of-fit plots for individual participants). The data and model predictions for exactly the same design (i.e., the same number of trials per condition) are averaged in the same way, so any distortions introduced by averaging apply equally.

Fig. 13

Goodness-of-fit results. (a) Response proportions (NR = nonresponse). (b) Response time percentiles (10th, 50th, and 90th). The data are shown with dashed lines and open points. The medians of the model predictions are shown with solid points; error bars show the corresponding 95% credible intervals. (c) Cumulative distribution functions. The data are shown with thick lines, with open points marking the 10th, 30th, 50th, 70th, and 90th percentiles. Model predictions are shown with thin lines and solid points, with the clusters of gray dots showing the uncertainty in the percentiles from 100 randomly selected samples from the joint posterior

Fig. 14

Goodness-of-fit results as a function of stop-signal delay (SSD). (a) Inhibition functions averaged over participants, as a function of 12 equal percentile ranges (8¹/₃% each). (b) Median response times for failed inhibitions (signal-response RT: SRRT) averaged over participants, as a function of 20 equal time intervals spanning the range of SSDs for each participant. The x-axis values are the average values of the ends of each range, with only every other range shown. The data are shown with solid points. The uncertainty of the model predictions resulting from 100 randomly selected samples from the joint posterior is shown with violin plots, with the white dots indicating the median of the predictions

Figure 13a and b (produced with the ggplot2 R package; Wickham, 2009; tutorial 5.5) show response proportions and RT distribution percentiles, respectively. Model predictions are accompanied by 95% CIs, and they indicate that the model describes the observed data well. Figure 13c provides a more complete characterization in terms of functions, showing the average cumulative probability of observing an RT; these functions asymptote at the probability of the response they represent (tutorials 3.2 and 4.4). Note that the sum of the asymptotes in each cell equals the probability of making any response; this is markedly less than 1 in the stop panels, on account of the frequency of successful stop trials, which have no associated RTs. Predictive uncertainty is indicated by clouds of points corresponding to the predictions for five percentiles using 100 samples from the joint posterior distribution. This more refined plot suggests a small misfit to the response probabilities, indicative of response bias unaccounted for by the model (e.g., accuracy in the hard condition is slightly overestimated for left responses and underestimated for right responses). If this misfit were consequential for an application, we might consider fitting an augmented model that allows different ex-Gaussian parameters for left- and right-stimulus runners. Modeling often involves an iterative process of refinement, aided by goodness-of-fit plots and the model selection methods described earlier.⁸ DMC supports this process at both the group and individual levels (see tutorial 5.3 and 5.6, respectively, and DMCpaper2.R).

Figure 14a shows that the model provides a good account of the average probability of failed inhibitions. Participants often have different ranges of SSDs over the same range of response probabilities, making it difficult to produce average inhibition functions that are representative of individual performance. As is explored in DMCpaper2.R, this is best addressed through effectively normalizing the domain of the functions by averaging equal percentile ranges of SSDs for each participant.⁹ Figure 14b shows good fit to the average median RTs for failed inhibitions.

From posteriors to priors

So far, we have described the process of combining priors with data to obtain posteriors. We can also complete the circle by using posteriors as a basis for developing priors to be used in the analysis of new data, thus realizing the promise of the Bayesian approach to build a quantitatively cumulative science (Jaynes & Bretthorst, 2003). Just like the likelihood, the prior is an important part of specifying a model (e.g., Lee & Vanpaemel, 2018), albeit one that is often more specific to particular designs, whereas the likelihood corresponds to a more generic part of the model that specifies the cognitive mechanisms that operate in a broad array of designs. Hence, we have provided functionality in DMC to facilitate the sharing of priors.

Table 4 provides the parameters of the best-fitting truncated normal distributions to the posterior distribution of the population mean and standard deviation parameters, as well as fits to the aggregated participant-level posterior samples. These parameters can provide starting points for specifying priors for similar experiments, perhaps after adjustment to account for changes in design and participant characteristics. Informative priors are particularly useful when the new experiment offers less constraint on estimation, because of a smaller sample size or a design change that results in the data providing less information about some aspects of the model (e.g., Osth, Jansson, Dennis, & Heathcote, 2018). Priors are crucial when using prior-predictive model selection methods such as Bayes factors (Kass & Raftery, 1995).

Table 4 Parameters of the best-fitting truncated normal distributions to the posterior distribution of the population mean (location) and standard deviation (scale) parameters, as well as fits to the aggregated participant-level posterior samples

DMC automates the process of obtaining fits to posterior distributions, and it allows the estimated parameters to be adjusted and the new priors plotted. For example, we might wish to expand the standard deviation of the priors in order to allow for uncertainty about the outcomes of future experiments. This is illustrated in Fig. 15, which shows the population-level and aggregated individual-level posteriors and the resulting priors with twice the estimated standard deviation. Heterogeneity among participants is evident in the aggregated individual posteriors, particularly in the μ parameter of the matching runners, for which some estimates are above 1 s. As expected, the priors for the mismatching τ parameters are largely uninformative in all cases.

Fig. 15

Priors (red lines) obtained from fitting the posterior distributions (black lines) with truncated normal distributions. (a) Population means. (b) Population standard deviations. (c) Aggregated individual posterior samples. The standard deviation of the priors has been doubled to allow for uncertainty about the outcomes of future experiments

Discussion

The models available in DMC are not for the faint-hearted; they are demanding of both the user and the data. The reward is that observed behavior can be mapped to meaningful psychological quantities. However, we believe that this almost magical process of inferring the values of latent variables should always be viewed with a degree of skepticism, as experience teaches us that magic is not the only thing that can happen. In the first part of this article, we described how to use the tools provided by DMC to ensure that in a particular application, a standard evidence-accumulation model, can be treated as a “measurement model”—that is, a model whose estimated parameters are meaningful because they can be uniquely mapped to the observed data up to some quantifiable degree of certainty. The same techniques can be applied to other standard models and also to newly developed models.

One of the design imperatives for DMC was to make it fairly straightforward to add new models (tutorials 2.3 and 2.4) that take advantage of the power and flexibility of the evidence-accumulation approach to modeling cognition. The emphasis on generality comes at the cost of speed and conformity to the standards required for an R package. However, we have also developed an R package that integrates with DMC and implements the standard DDM and LBA in C++, thus speeding sampling by up to an order of magnitude (Lin & Heathcote, 2017). Although this faster approach requires C++ programming skills, we envisage that in the future it will be expanded to other frequently used models.

In the second part of the article, we illustrated the benefits of DMC’s flexibility and generality, outlining how more advanced applications of DMC enable the standard models to be integrated into a hierarchical framework that addresses commonalities among individuals, and how standard models can be used as building blocks for more wide-ranging models of cognition, with an example application to a real data set. We demonstrated that contingent choices in the stop-signal paradigm can be successfully modeled by a simple and mathematically tractable parallel-race architecture. In many cases, this approach straightforwardly extends to more complex tasks and logical contingencies, creating a powerful framework to model latent cognitive structures in a broad array of applications. An example—also implemented in DMC—is Strickland, Loft, Remington, and Heathcote’s (2018; https://osf.io/t3cqw) prospective memory decision control model that instantiates feedforward competitive interactions between a two-choice decision and an alternative third choice. Similarly, the mixture-modeling approach we used to account for attention failures in the stop-signal race model is also implemented in Castro, S., Strayer, D., Matzke, D. & Heathcote, A. (submitted). Cognitive workload measurement and modelling under divided attention. Journal of Experimental Psychology: General; https://osf.io/e8kag) DMC model of response omissions under dual-task load.

One issue with such elaborations of the standard models is that they often lack a computed likelihood, which is the key element for tractable Bayesian estimation. Fortunately, new simulation-based approaches can support Bayesian estimation even in these cases, greatly expanding the ability to model complex cognitive processes. DMC includes a general implementation of one of these, probability density approximation (Holmes, 2015; Turner & Sederberg, 2014), with an example using Holmes et al.’s (2016) Piecewise LBA that can serve as a basis for developing further applications (tutorial 2.4). Because this approach is computationally intensive, we are working on a C and GPU implementation that can be called by DMC through an R package (Lin, Y-S., Heathcote, A. & Holmes, W.R. (submitted). Parallel probability density approximation, Behavior Research Methods).

In closing, we emphasize that DMC not only provides a framework for implementing models but also a means to explore their strengths and weaknesses. We believe it is crucial to thoroughly test the usefulness of a new model and/or design before placing faith in results from empirical data. We also believe it is important for users to have thorough understanding of the estimation process and the behavior of the model before applying it to real data. To encourage this, DMC’s functionality is documented through an extensive series of tutorials that provide hands-on experience with simulated data. We hope that after working through the tutorials, even those relatively new to these models will be able to use them with confidence. For those new to quantitative modeling, we also recommend the excellent introductions by Farrell and Lewandowsky (2015) and Lee and Wagenmakers (2013). Because DMC is open-source, experienced users can inspect, verify, and modify its functions as they require. We regularly update the OSF distribution, and we encourage others to develop their own extensions, by either integrating elements of the code into their applications or incorporating DMC into their OSF projects, along with their own modifications and tutorials to enable others to replicate their analyses.

Author note

A.H., L.S., and M.G. are supported by Grant ARC DP160101891. D.M. is supported by a Veni grant (451-15-010) from the Netherlands Organization of Scientific Research (NWO).